HHU暑期第一弹——小小小数论(欧拉函数+埃式筛法+分解质因数+欧几里得算法+扩展欧几里得算法和模线性方程)
第一弹数论的主要内容有以下几部分:欧拉函数、埃式筛法、分解质因数、欧几里得算法、扩展欧几里得算法和模线性方程。
1、欧拉函数(连续求n个数的欧拉函数)
#include
using namespace std;
int main()
{
int phi[100];// 用于筛法开素数表
int dive[100];//用于储存1~n的每个数的欧拉函数
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
phi[i]=i;
}
for(int i=2;i*i<=n;++i)
{
if(phi[i]==i)
{
for(int j=i*i;j<=n;j+=i)
{
phi[j]=i;
}
}
}
dive[1]=1;
for(int i=2;i<=n;++i)
{
dive[i]=dive[i/phi[i]];
if((i/phi[i])%phi[i]==0)
{
dive[i]*=phi[i];
}
else
{
dive[i]*=phi[i]-1;
}
}
for(int i=2;i<=n;i++)
cout< 求单个数的欧拉函数:
int n,i,temp;
while(scanf("%d",&n)!=EOF)
{
temp=n;
for(i=2;i*i<=n;i++)
{
if(n%i==0)
{
while(n%i==0) n=n/i;
temp=temp/i*(i-1);
}
if(n1)
temp=temp/n*(n-1);
printf("%d\n",temp);
} 2、埃式筛法(用于打印素数表)
给出要筛数值的范围n,找出以内的素数。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个质数,也就是3筛,把3留下,把3的倍数剔除掉;接下去用下一个质数5筛,把5留下,把5的倍数剔除掉;不断重复下去.....
#include
#include
#include
using namespace std;
int vis[10000];
int main()
{
int n;
cin>>n;
int m=sqrt(n+0.5);
memset(vis,0,sizeof(vis));
for(int i=2;i<=m;i++)
{
if(!vis[i])
{
for(int j=i*i;j<=n;j+=i)
{
vis[j]=1;
}
}
}
for(int i=2;i<=n;i++)
{
if(vis[i]==0)//最后剩下的vis[i]=0的都是质数
cout< 下面贴一个埃式筛法的形象的展示:
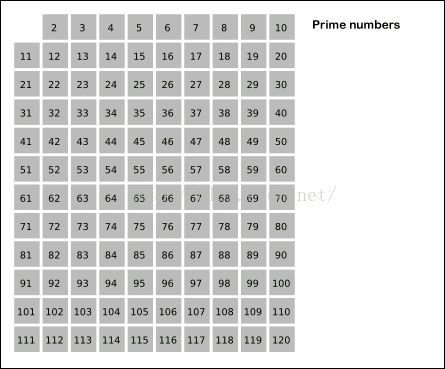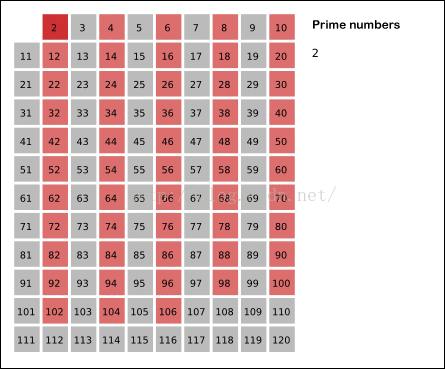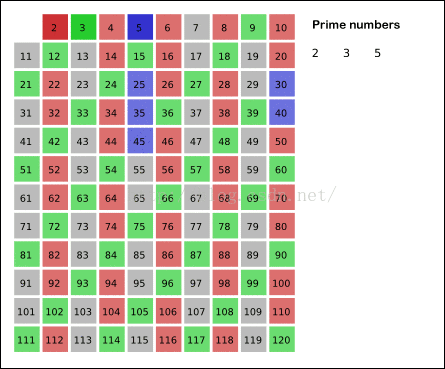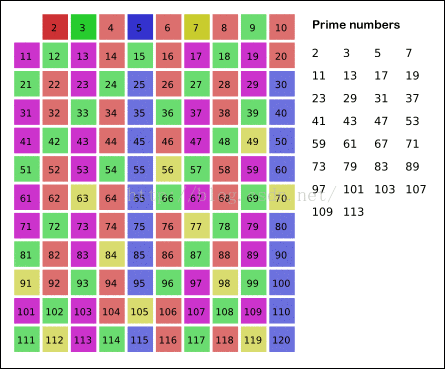
3、分解质因数(模板)
#include
#include
using namespace std;
int a[10000];//用于储存第i个质因数的值
int b[10000];//用于储存第i个质因数的指数
int main()
{
int n;
cin>>n;
int tot;//不同质因数的个数
int temp, i,now;
temp=(int)((double)sqrt(n)+1);
tot=0;
now=n;
for(i=2;i<=temp;++i)
{
if(now%i==0)
{
a[++tot]=i;
b[tot]=0;
while(now%i==0)
{
++b[tot];
now/=i;
}
}
}
if(now!=1)
{
a[++tot]=now;
b[tot]=1;
}
//得到a[i]^b[i]就是n的质因数分解
} 4、欧几里得算法 //辗转相除法
欧几里德算法又称辗转相除法,用于计算两个整数a,b的最大公约数。
基本算法:设a=qb+r,其中a,b,q,r都是整数,则gcd(a,b)=gcd(b,r),即gcd(a,b)=gcd(b,a%b)。
证明:
a可以表示成a = kb + r,则r = a mod b
假设d是a,b的一个公约数,则有 d|a, d|b,而r = a - kb,因此d|r 因此d是(b,a mod b)的公约数
假设d 是(b,a mod b)的公约数,则 d | b , d |r ,但是a = kb +r 因此d也是(a,b)的公约数
因此(a,b)和(b,a mod b)的公约数是一样的,其最大公约数也必然相等,得证
求最大公约数:
int gcd(int a,int b)
{
return b ? gcd(b,a%b) : a;
}求最小公倍数:
- int lcm(int a,int b) {
- return a/gcd(a,b)*b;
- }
5、扩展欧几里得算法
对于一个等式,a*x+b*y=gcd(a,b),求一对x,y的算法。
证明:设 a>b。
1,显然当 b=0,gcd(a,b)=a。此时 x=1,y=0;
2,ab!=0 时 设 ax1+by1=gcd(a,b); bx2+(a mod b)y2=gcd(b,a mod b);
根据朴素的欧几里德原理有 gcd(a,b)=gcd(b,a mod b);
则:ax1+by1=bx2+(a mod b)y2; 即:ax1+by1=bx2+(a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;
根据恒等定理得:x1=y2; y1=x2-(a/b)*y2;
这样我们就得到了求解 x1,y1 的方法:x1,y1 的值基于 x2,y2.
上面的思想是以递归定义的,因为 gcd 不断的递归求解一定会有个时候 b=0,所以递归可以结束。
int ex_gcd(int a,int b,int &x,int &y)//x、y传地址的意思是,函数内对x、y的改变也能改变函数外x、y的值,类似于全局变量
{
if(b==0)
{
x=1;
y=0;
return a;
}
int r=ex_gcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
return r;
}6、模线性方程
ax ≡ b(mod n),表示ax和b对n取模相等。
1)求解线性不定方程
ax + by = c
先求出一组解,然后考虑如何表示通解,设d = gcd(a, b), 假设c不是d的倍数,则左边是d的倍数而右边不是,则方程无解,所以方程有解当且仅当d | c.设c = c' * d。
我们先考虑方程 ax + by = d,这样由扩展gcd便可求出一组解 (x', y'),则(c'x', c'y')就是原方程的一组解,然后考虑通解:假设有两组解(x1, y2) , (x2, y2),有 ax1 + by1 == ax2 + by2 = c, 移项得: a(x1 - x2) == b(y2 - y1),消去d后有 a'(x1 - x2) == b'(y2 - y1)。此时a' 和 b' 互素,所以(x1 - x2)一定是b'的倍数,而(y2 - y1)一定是a'的倍数,由此可得到通解:给一组特解(x, y), 通解为(x - kb', y + ka')。
2)求解模线性方程
ax = b(mod n)
其实方程等价于 ax - ny = b, 标准模线性方程,但是得考虑剩余系。
算法导论上有两个定理:
定理一:设d = gcd(a, n), 假定对整数x', y', 有d = ax' + ny', 如果d | b, 则方程ax = b(mod)有一个解的值为x0, 满足:、
x0 = x'(b / d)(mod n)
定理二:假设方程ax = b(mod n)有解, x0是方程的任意一个解, 则方程对模n恰有d个不同的解, 分别为: xi = x0 + i * (n / d), 其中 i = 1,2,3......d - 1
有了这两个定理, 解方程就不难了。
void linear_mod_equation (int a, int b, int n, int *sol)
{
int d, x, y;
gcd (a, n, d, x, y );
if (b % d) d = 0;
else
{
sol [0] = x * ( b / d ) % n ;
for (int i = 1; i < d; ++i)
sol[i] = (sol[i - 1] + n / d) % n;
}
}long long inv(ll a, ll n)
{
long long d, x, y;
gcd(a, n, d, x, y);
return d == 1 ? (x % n + n) % n : -1;
}首先看一个简单的例子:
5x=4(mod3) 解得x = 2,5,8,11,14.......
由此可以发现一个规律,就是解的间隔是3.那么这个解的间隔是怎么决定的呢?
如果可以设法找到第一个解,并且求出解之间的间隔,那么就可以求出模的线性方程的解集了.
我们设解之间的间隔为dx.那么有a*x = b(mod n); a*(x+dx) = b(mod n);
两式相减,得到: a*dx(mod n)= 0;
也就是说a*dx就是a的倍数,同时也是n的倍数,即a*dx是a 和 n的公倍数.为了求出dx,我们应该求出a 和 n的最小公倍数,此时对应的dx是最小的。
设a 和 n的最大公约数为d,那么a 和 n 的最小公倍数为(a*n)/d. 即a*dx = a*n/d; 所以dx = n/d. 因此解之间的间隔就求出来了.
bool modular_linear_equation(int a,int b,int n)
{
int x,y,x0,i;
int d=exgcd(a,n,x,y);
if(b%d)
return false;
x0=x*(b/d)%n; //特解
for(i=1;i