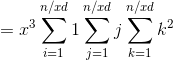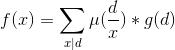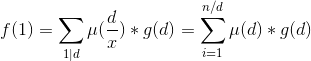南昌邀请赛网络赛 G. tsy's number(莫比乌斯反演+线性筛)
题目链接:
tsy's number
题意:
思路:
原式 =
设T = id ,将 i 的求和变为 T 的求和:
![]() :这个是
:这个是![]() 与
与 ![]() 的迪利克雷卷积,并且g(x)与f(x)均为积性函数,因此该函数也为积性函数,可通过线性筛O(n)求解。
的迪利克雷卷积,并且g(x)与f(x)均为积性函数,因此该函数也为积性函数,可通过线性筛O(n)求解。
处理上述积性函数前缀和,对原式前半部分的 ![]() 进行数论分块即可,单次询问复杂度 O(sqrt(n)) 。
进行数论分块即可,单次询问复杂度 O(sqrt(n)) 。
线性筛:
1. i = p,p为质数时,![]()
2. i 为合数:
i%prime[j] != 0:![]()
i%prime[j] == 0:分两种情况:
<1> i 中只有一个prime[j]的因子:
![]()
<2> i 中存在 ![]() 的因子,k>=2
的因子,k>=2
![]()
i%prime[j] == 0要分两种情况是因为![]() 中,(T/d)可能%p == 0,可能 != 0 。
中,(T/d)可能%p == 0,可能 != 0 。
若 i % p ==0 ,![]()
若 i % p !=0 ,![]()
Tips:![]() 与2和6不互质,除以2,除以6的时候不能算逆元。
与2和6不互质,除以2,除以6的时候不能算逆元。
Code:
#include
using namespace std;
typedef long long ll;
const int MAX = 1e7 + 10;
const ll inf = 1e18;
const ll mod = 1ll << 30;
ll m, n, p;
ll prime[MAX + 10], sum[MAX + 10];
int vis[MAX + 10];
void init()
{
memset(vis, 0, sizeof(vis));
sum[1] = 1;
int tot = 0;
for (int i = 2; i <= MAX; i++) {
if (!vis[i]) {
prime[++tot] = i;
sum[i] = 1ll * i * i%mod*i%mod*(i - 2) % mod;
}
for (int j = 1; j <= tot && i*prime[j] <= MAX; j++) {
vis[i*prime[j]] = 1;
if (i%prime[j] == 0) {
if ((i / prime[j]) % prime[j] != 0) {
ll tmp1 = sum[i / prime[j]] * prime[j] % mod*prime[j] % mod*prime[j] % mod*(prime[j] - 1) % mod*prime[j] % mod*prime[j] % mod*prime[j] % mod*prime[j] % mod;
ll tmp2 = sum[i / prime[j]] * prime[j] % mod*prime[j] % mod*prime[j] % mod*(prime[j] - 1) % mod*prime[j] % mod*prime[j] % mod*prime[j] % mod;
sum[i*prime[j]] = (tmp1 - tmp2 + mod) % mod;
}
else {
sum[i*prime[j]] = sum[i] * prime[j] % mod*prime[j] % mod*prime[j] % mod*prime[j] % mod;
}
break;
}
else {
sum[i*prime[j]] = sum[i] * sum[prime[j]] % mod;
}
}
}
for (int i = 1; i <= MAX; i++) {
sum[i] = (sum[i] + sum[i - 1]) % mod;
}
}
int main()
{
int T;
scanf("%d", &T);
init();
while (T--)
{
ll n;
scanf("%lld", &n);
ll ans = 0;
ll pos = 0;
for (int i = 1; i <= n; i = pos + 1) {
pos = n / (n / i);
ll w = n / i;
ll tmp1 = (1 + w) *w / 2 % mod;
ll tmp2 = w * (w + 1) / 2;
if (tmp2 % 3 == 0) tmp2 = tmp2 / 3 % mod*(2 * w + 1) % mod;
else tmp2 = tmp2 % mod*((2 * w + 1) / 3 % mod) % mod;
ll tmp = w * tmp1%mod*tmp2%mod;
ans = (ans + (sum[pos] - sum[i - 1] + mod) % mod*tmp%mod) % mod;
}
printf("%lld\n", ans);
}
return 0;
}
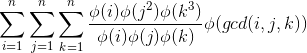
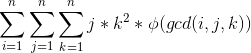
![=\sum_{d=1}^{n}\phi (d)\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{k=1}^{n}j*k^{2}[gcd(i,j,k)=d]](http://img.e-com-net.com/image/info8/83e428448c154235a1b03eb3063077ee.gif)
![=\sum_{d=1}^{n}\phi (d)*d^{3}\sum_{i=1}^{n/d}\sum_{j=1}^{n/d}\sum_{k=1}^{n/d}j*k^{2}[gcd(i,j,k)=1]](http://img.e-com-net.com/image/info8/07984bad06c0481caa8797e6bc9af307.gif)
![f(x)=\sum_{i=1}^{n/d}\sum_{j=1}^{n/d}\sum_{k=1}^{n/d}j*k^{2}[gcd(i,j,k)=x]](http://img.e-com-net.com/image/info8/b0cefe4dce1d48ba81fee753e5ab8511.gif)
![g(x)=\sum_{x|d}^{ }f(d)=\sum_{i=1}^{n/d}\sum_{j=1}^{n/d}\sum_{k=1}^{n/d}j*k^{2}[x|gcd(i,j,k)]](http://img.e-com-net.com/image/info8/a0f730eb540b484f88f0b8cf9610b894.gif)
![=\sum_{i=1}^{n/xd}\sum_{j=1}^{n/xd}\sum_{k=1}^{n/xd}j*k^{2}[1|gcd(i,j,k)]*x^{3}](http://img.e-com-net.com/image/info8/2582ce725ba741ba8b2272bceb7537df.gif)