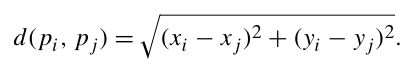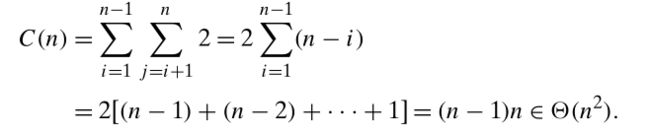Brute force and exhaustive search

           Brute force and exhaustive search（蛮力和彻底搜索）

    Brute force is a straightforward approach to solving a problem, usually directly based on the problem statement and definitions of the concepts involved.Just do it!” would be another way to describe the prescription of the brute-force approach.

Burte force--直接计算

 

The author attempts to give some motivation to this chapter:

1. Brute force is applicable to a wide variety of problems.（暴力适用于各种各样的问题。）

2. For some problems does generate reasonable algorithm.（因为有些问题确实产生了合理的算法。）

3. If the problem is only infrequently solved then the expense of developing a better algorithm is not justified.（如果这个问题只是很少被解决，那么开发一个更好的算法的费用是不合理的。）

4. The brute force algorithm may be good for small problem size.（蛮力算法可以很好地解决小问题。）

5. Brute force can be used for comparison of more sophisticated algorithms.（蛮力可以用来比较更复杂的算法。）

---------------------------------------------------------------------------------------------------------------------------

3.1 selection sort and bubble sort（选择排序和冒泡排序）

 we consider the application of the brute-force approach to the problem of sorting: given a list of n orderable items (e.g., numbers, characters from some alphabet, character strings), rearrange them in nondecreasing order.

3.1.1 selection sort (选择排序）

算法实现过程：

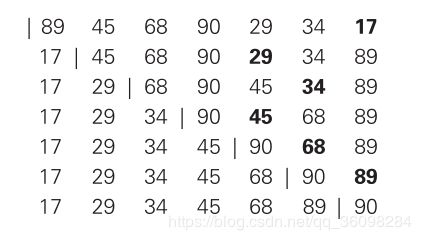
步骤1：We start selection sort by scanning the entire given list to find its smallest element and exchange it with the first element, putting the smallest element in its final position in the sorted list.

步骤二：Then we scan the list, starting with the second element,to find the smallest among the last [n − 1]elements and exchange it with the second element,putting the second smallest element in its final position.

 

                        

例子：初始：89 45 68 90 29 34 17 。一共扫描（遍历）序列7次，移动数据7次。总的遍历＋比较的次数是C（n），因此复杂度是O(N^2).

                              

         
选择排序中文详解（点击）

 

3.1.2 Bubble sort （冒泡排序）

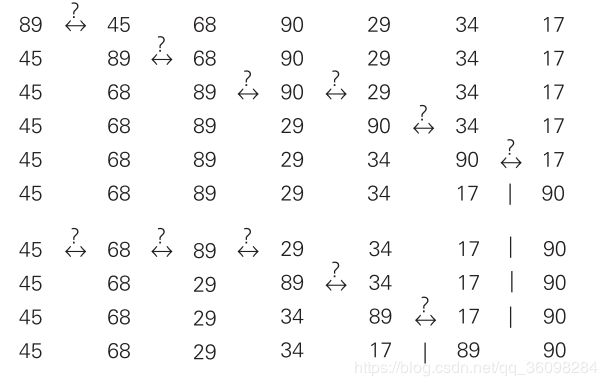
 1）定义：compare adjacent elements of the list and exchange them if they are out of order（比较列表中的相邻元素，如果它们无序（一般小数在左侧，大数在右侧），则进行交换）

2）排序过程：By doing it repeatedly, we end up “bubbling up” the largest element to the last position on the list. The next pass bubbles up the second largest element, and so on, until after n − 1 passes the list is sorted（我们最终将最大的元素“冒泡”到列表中的最后一个位置。下一个步骤向上冒泡第二大元素，依此类推，直到n-1通过之后，列表才被排序。）

3）例子;第一次是如何把90换到最后的，第二次如何把89换到倒数第二个位置的

                    

4）时间复杂度O（N^2）

                     

 

冒泡排序中文详解（点击）

---------------------------------------------------------------------------------------------------------------------------

3.2 sequential search and brute-force string matching

3.2.1 sequential search(顺序搜索）

   该查找法就如同数组的遍历，从数组的第一个元素开始，检查数组的每一个元素，以便确定是否有查找的数据。

                

详细参考

3.2.2 Brute-force string matching（蛮力字符串匹配）

Searching for a pattern,--- P[0...m-1]；in text----T[0...n-1]

在 text 的给定字符串中对patter进行匹配，顺序、字符个数均需相同，因此注意for循环时的截止位置：n-m

                          

 

Illustrate the algorithm

Worst case when a shift is not made until the m-th comparison, so Θ(nm)

Typically shift is made early then Average case Θ(n) or for m << n

---------------------------------------------------------------------------------------------------------------------------

3.3 Closest-pair and convex-hull problems by brute force

3.3.1 Closest-pair problems

1）描述：该问题是求n个点中，最短距离的两个点的距离。

2）两点间距离公式的计算：

                      

3）算法: compute the distance between each pair of distinct points and find a pair with the smallest distance

    &we do not want to compute the distance between the same pair of points twice.（不想算重的办法） To avoid doing so, we consider only the pairs of points (p i , p j ) for which i < j.（选取的两个点的角标有明确的关系，即i < j）

    &同时，开根号是个繁琐的工作同时得到的数字也是估计值，因此在正常的算法中我们可以只计算(x i − x j ) 2 + (y i − y j ) 2，省略开根号的操作，比较这个和的最小值即可

4）时间复杂度

                    

 

3.3.2 Convex-Hull Problem

 

 

---------------------------------------------------------------------------------------------------------------------------

3.4 Exhausive Search

   许多这样的问题是优化问题：他们要求找到一个元素，最大化或最小化一些期望的特性，如路径长度或分配成本。Many such problems are optimization problems: they ask to find an element that maximizes or minimizes some desired characteristic such as a path length or an assignment cost.

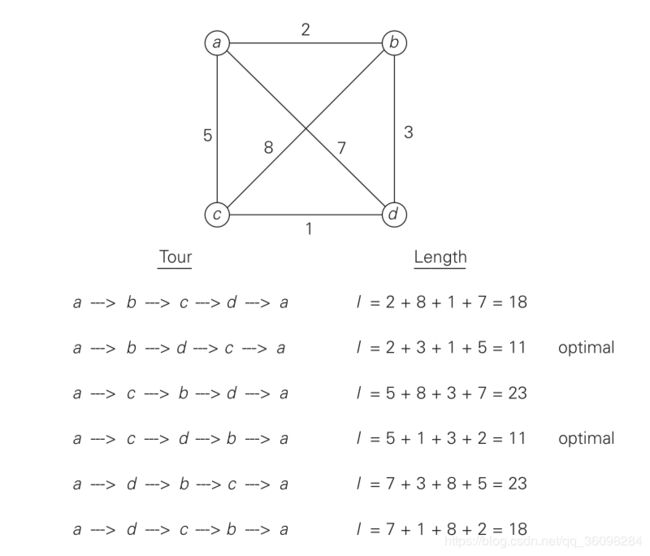
3.4.1 Travelling salesman Problem

1）问题描述：

     TSP问题（旅行商问题）是指旅行家要旅行n个城市，要求各个城市经历且仅经历一次然后回到出发城市，并要求所走的路程最短。 In layman’s terms, the problem asks to find the shortest tour through a given set of n cities that visits each city exactly once before returning to the city where it started.

                     

2）解决办法：

It is easy to see that a Hamiltonian circuit can also be defined as a sequence of n + 1adjacentverticesv i 0 , v i 1 , . . . , v i n−1 , v i 0 ,wherethefirstvertexofthesequence is the same as the last one and all the other n − 1 vertices are distinct 很容易看出，哈密顿电路也可以定义为N+1相邻垂直v i 0，v i 1，.…，V i n−1，V i 0，其中序列的第一个顶点与最后一个相同，所有其他n-1顶点都是不同的

Thus, we can get all the tours by generating all the permutations of n − 1intermediate cities, compute the tour lengths, and find the shortest among them   因此，我们可以得到通过生成n-1个中间城市的所有排列，计算行程长度，并找出其中最短的

The problem can be conveniently modeled by a weighted graph, with the graph’s vertices representing the cities and the edge weights specifying the distances. 该问题可以通过加权图方便地建模，图的顶点表示城市，边权指定距离。

 

3.4.2 Knapsack Problem

蛮力法解决背包问题。详细参考：https://blog.csdn.net/qq_36098284/article/details/98664290

 

3.4.3 Assignment Problem

1）问题描述：

There are n people who need to be assigned to execute n jobs, one person per job

 The cost that would accrue if the ith person is assigned to the jth job is a known quantity C[i, j]for each pair i, j 

                      

 the problem is to select one element in each row of the matrix so that all selected elements are in different columns and the total sum of the selected elements is the smallest possible.

下面列举一些：

                

---------------------------------------------------------------------------------------------------------------------------

3.5 Depth-First Search an Breadth-First Search

3.5.1 Depth-First Search(DFS)

1）思想&方法：

深度优先算法从任意一点开始；

（Depth-first search starts a graph’s traversal at an arbitrary vertex by marking it as visited）

 

每一次迭代访问的时候，算法都是使得一个未曾访问过的节点并且和当前存在的节点邻接的节点进入队列或者栈内； 

（On each iteration, the algorithm proceeds to an unvisited vertex that is adjacent to the one it is currently in.）

 

这种迭代一直继续直到一个死亡：所有的邻接节点都被访问过的时候。

（This process continues until a dead end—avertex with no adjacent unvisited vertices— is encountered.）

 

在遇到死亡节点的时候，算法回到该死亡节点的上一个节点，继续访问该节点的邻接节点，直到它的全部邻接节点全部访问完，再往上一层回溯，直到返回到初始节点 

（At a dead end, the algorithm backs up one edge to the vertex it came from and tries to continue visiting unvisited vertices from there）

 

如果返回到初始节点后，仍有为被访问过的节点，则重新选择初始节点，重新开始，继续遍历，直到结束

（If unvisited vertices still remain, the depth-first search must be restarted at any one of them.）

 

使用栈来实现

（It is convenient to use a stack to trace the operation of depth-first search）

 

当节点被第一次访问的时候，进栈；当它变成一个死亡的时候，出栈；

（We push a vertex onto the stack when the vertex is reached for the first time；and we pop a vertex off the stack when it becomes a dead end）

 

  当未被访问过的节点第一次被访问的时候，他成为之前节点的孩子节点。这样连接的边叫做tree edge 。同时这些边构成了森林

（Whenever a new unvisited vertex is reached for the first time, it is attached as a child to the vertex from which it is being reached. Such an edge is called a tree edge because the set of all such edges forms a forest. ）

 

该算法还可能遇到一条边，该边指向一个以前访问过的顶点，而不是它的直接前一个顶点。这样的边叫 back edge，因此他连接是该节点和其祖先节点，而不是父节点；

（The algorithm may also encounter an edge leading to a previously visited vertex other than its immediate predecessor (i.e., its parent in the tree).Such an edge is called a back edge because it connects a vertex to its ancestor, other than the parent, in the depth-first search forest.）

 

使用邻接矩阵和邻接表

（adjacency matrix or adjacency lists.）

 

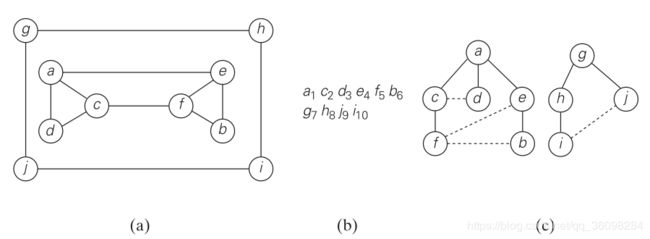
2 例子：

 遍历结果：a c d f b e / g h i j 

 

3）代码实现

                                 

                                         

 

4）时间复杂度

Thus, fortheadjacency matrix representation, the traversal time is in O(|V| ^2 ), and for the adjacency list representation, it is in O(|V| + |E|) where |V| and |E| are the number of the graph’s vertices and edges, respectively.

 

5）更多详细参考（代码）

中文详细参考:  https://blog.csdn.net/qq_36098284/article/details/98885064

---------------------------------------------------------------------------------------------------------------------------

3.5.2 Breadth-First Search（BFS）

1）思想&方法：

它的进程首先访问与起点相邻的所有顶点的同心方式。然后所有未访问的顶点，两条边分开，依此类推，直到全部的顶点以相同的连接方式被全部访问。

It proceedsin a concentric manner by visiting first all the vertices that are adjacent to a starting vertex, then all unvisited vertices two edges apart from it, and so on, until all the vertices in the same connected component as the starting vertex are visited.

 

如果仍有未访问的顶点，则必须在图中另一个连接组件的任意顶点。

If there still remain unvisited vertices, the algorithm has to be restarted at an arbitrary vertex of another connected component of the graph.

 

使用队列这个数据结构。在每次迭代中，算法找到与前顶点相邻的所有未访问顶点，将它们标记为已访问，并将它们添加到队列中；之后，队列最前方的顶点需要从队列中被删除。

On each iteration, the algorithm identifies all unvisited vertices that are adjacent to the front vertex, marks them as visited, and adds them to the queue; after that, the front vertex is removed from the queue.

 

同样也有tree edge 和 cross edge，和DFS算法相同

 

2）例子：

       

 

3) 代码

                          

 

4）时间复杂度

Breadth-first search has the same efficiency as depth-first search: it is in O(|V| 2 ) for the adjacency matrix representation and in O(|V| + |E|) for the adjacency list representation

 

5）应用

用于寻找两个顶点直接最短的距离   ，DFS算法不可

例如，bfs可用于查找两个给定顶点之间边数最少的路径。为此，我们在两个顶点之一处开始BFS遍历，并在到达另一个顶点时立即停止。

   For example, BFS can be used for finding a path with the fewest number of edges between two given vertices. To do this, we start a BFS traversal at one of the two vertices and stop it as soon as the other vertex is reached. 

 

例如，图3.12中图表中的路径a−b−c−g在顶点a和g之间的所有路径中的边数最少。

 For example, path a − b − c − g in the graph in Figure 3.12 has the fewest number of edges among all the paths between vertices a and g. 

                              

6）更多详细参考（代码）

中文详细参考：https://blog.csdn.net/qq_36098284/article/details/98890052

---------------------------------------------------------------------------------------------------------------------------

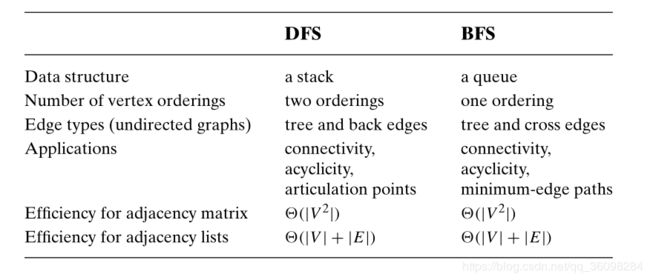
3.5.3 DFS & BFS 的区别

                  

---------------------------------------------------------------------------------------------------------------------------

最近更新时间是2019.8.9

持续更新！！！！！！