素数的筛选

【穷举法】

这种方法的枚举部分的复杂度是 $O(n)$，而判断素数的复杂度是 $O(\sqrt{n})$，因此总复杂度是 $O(n\sqrt{n})$。这个复杂度对 $n$ 不超过 $10^5$ 的大小是没有问题的，代码如下：

int tot;			// tot用来统计素数的个数
int p[maxn];		// 数组p用来存放素数
bool prime[maxn];	// 数组prime用来判断是否为素数，true是素数，false不是素数

void make_prime()
{
	for(int i = 2; i <= n; i++)
	{
		bool flag = true;
		for(int j = 2; j * j <= i; j++)
		{
			if(i % j == 0)
			{
				flag = false;
				break;
			}
		}
		if(flag == true)
		{
			prime[i] = true;	//是素数
			p[tot++] = i;		//则把i存入p数组
		}
	}
}

【Eratosthenes筛法】

埃拉托斯特尼(Eratosthenes)筛法，简称埃氏筛，是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定素数的算法。

思想：一个素数的倍数都不是素数。初始时，先假设所有数都是素数，从 $2$ 开始枚举，当找到一个素数时，显然这个素数乘上另外一个数之后都是合数，把这些合数都筛掉，继续向下枚举，直至所有数枚举完毕。

int tot = 0;		// tot用来统计素数的个数
int p[maxn];		// 数组p用来存放素数
bool prime[maxn];   // 数组prime用来判断是否为素数，false为素数，true为合数

void make_prime()
{
	for(int i = 2; i <= N; i++)
	{
		if(!prime[i])  							// 如果i是素数
		{
			p[tot++] = i;
			for(int j = 2 * i; j <= N; j += i)   // 如果i是素数，则i * j不是素数
				prime[j] = true;
		}
	}
}

此筛选法的时间复杂度是 $O(nloglogn)$， 空间复杂度是 $O(n)$

另外，可以发现，$2$ 和 $3$ 都会把 $6$ 标记为合数。实际上，小于 $x^2$ 的 $x$ 的倍数在扫描更小的数时就已经被标记过了。

所以做一个小的优化：对于每个数 $x$，我们只需要从 $x^2$ 开始，把 $x^2、(x+1)\ast x\dots \lfloor N/x\rfloor \ast x$ 标记为合数即可。

int p[N], cnt;		// 数组p用来存放素数
bool st[N];			// 数组st用来判断是否为素数，false为素数，true为合数

void get_primes()
{
    for(int i = 2; i <= N; ++i)
    {
        if(!st[i])
        {
            p[cnt++] = i;
            for(int j = i; j <= N / i; j ++)
                st[i * j] = true;
        }
    }
}

【Euler筛法】

即使在优化后（从 $x^2$ 开始），埃氏筛仍然会重复标记合数。例如 $12$ 既会被 $2$ 又会被 $3$ 标记，在标记 $2$ 的倍数时，$12=6\ast 2$，在标记 $3$ 的倍数时，$12=4\ast 3$。其根本原因是我们没有确定出唯一的产生 $12$ 的方式。

按照这个思想，我们在生成一个需要标记的合数时，每次只向现有的数中乘上一个质因子，并且让它是这个合数的最小质因子。这相当于让合数的质因子从大到小累积，即让 $12$ 只有 $3\ast 2\ast 2$ 一种产生方式。具体地说，我们采用如下的线性筛法，每个合数只会被它的最小质因子筛一次，时间复杂度为 $O(N)$。

int tot = 0;		//tot用来统计素数的个数
int p[maxn];		//数组p用来存放素数
bool prime[maxn];   //数组prime用来判断是否为素数，false为素数，true为合数

void make_prime()
{
	for(int i = 2; i <= N; i++)
	{
		if(!prime[i])
			p[tot++] = i;
		for(int j = 0; j<tot && i*p[j]<=N; j++)
		{
			prime[i*p[j]] = true;
			if(i%p[j]==0)	break;	//优化的关键
		}
	}
}

if(i%p[j]==0) break; 这个是优化的关键。实在不理解的话，那就和本蒟蒻一样，跟着循环跑一遍吧 TAT

【例题】

AcWing 868. 筛质数（埃氏筛模板）

题目链接：点击这里

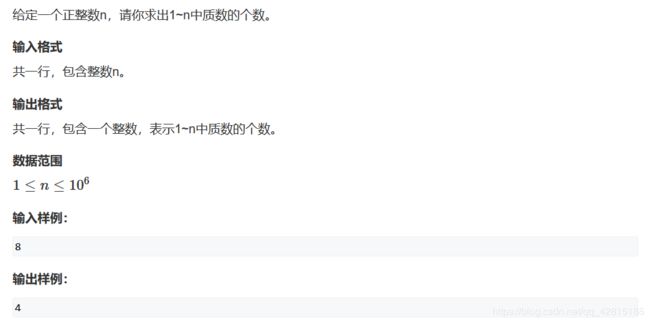
时间复杂度是 O(nloglogn)， 空间复杂度是 O(n)

#include
#include
#include

using namespace std;
const int N = 1e6 + 10;

int primes[N], cnt;		// primes[]存储所有素数
bool st[N];				// st[x]存储x是否被筛掉

void get_primes(int n)
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i])
        {
            primes[cnt++] = i;
            for(int j = i + i; j <= n; j += i)  st[j] = true;
        }
    }
}

int main()
{
    int n;
    scanf("%d", &n);
    
    get_primes(n);
    
    printf("%d\n", cnt);
    
    return 0;
}

AcWing 868. 筛质数（线性筛模板）

题目链接：点击这里

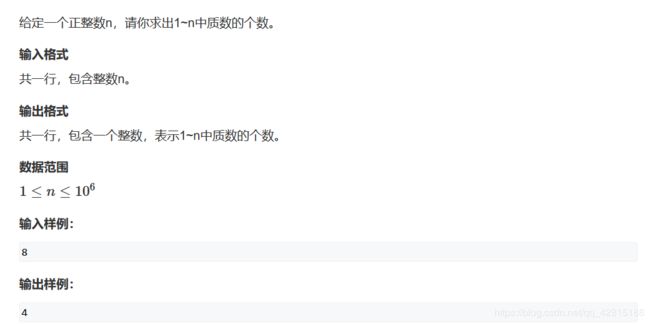
时间复杂度为 O(N)

每个合数只会被它的最小质因子筛掉：

1. i%primes[j]==0，说明primes[j]一定是i的最小质因子，primes[j]一定是 primes[j] * i 的最小质因子

2. i%primes[j]!=0，说明primes[j]一定小于i的所有质因子，primes[j]也一定是 primes[j] * i 的最小质因子

#include
#include
#include

using namespace std;
const int N = 1e6 + 10;

int primes[N], cnt;		// primes[]存储所有素数
bool st[N];				// st[x]存储x是否被筛掉

void get_primes(int n)
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i])  primes[cnt++] = i;
        for(int j = 0; primes[j] <= n / i; ++j)
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0)  break;
        }
    }
}

int main()
{
    int n;
    scanf("%d", &n);
    
    get_primes(n);
    
    printf("%d\n", cnt);
    
    return 0;
}

HDU 2098 分拆素数和

题目链接：点击这里

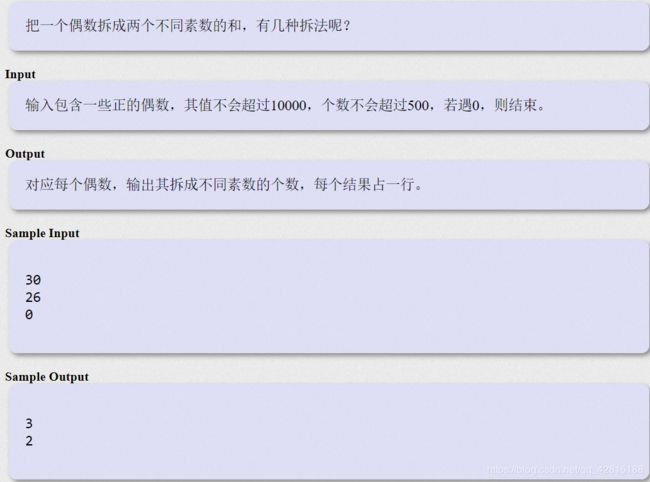
注意是把一个偶数分解成两个不同的素数，比如 26 = 13 + 13 这个答案就是错误的。

被自己蠢哭，打好的素数表在主函数里忘调用了QAQ

AC代码：

#include
#include
#include
#include

using namespace std;
typedef long long ll;
const int N = 10010;

bool st[N];					// st[x]存储x是否被筛掉

void get_prime(int n)
{
	for(int i = 2; i <= n; i++)
	{
		if(!st[i])
		{
			for(int j = 2 * i; j <= n; j += i)	st[j] = true;
		}
	}
}

int main()
{
	get_prime(N - 1);
	
	int n;
	while(scanf("%d", &n) != EOF && n)
	{
		int cnt = 0;
		
		for(int i = 2; i < n / 2; i++)
			if(!st[i] && !st[n - i])	cnt++;
		
		printf("%d\n", cnt);
	}
	return 0;
}

牛客 A. Forsaken喜欢数论（求最小质因子）

题目链接：点击这里

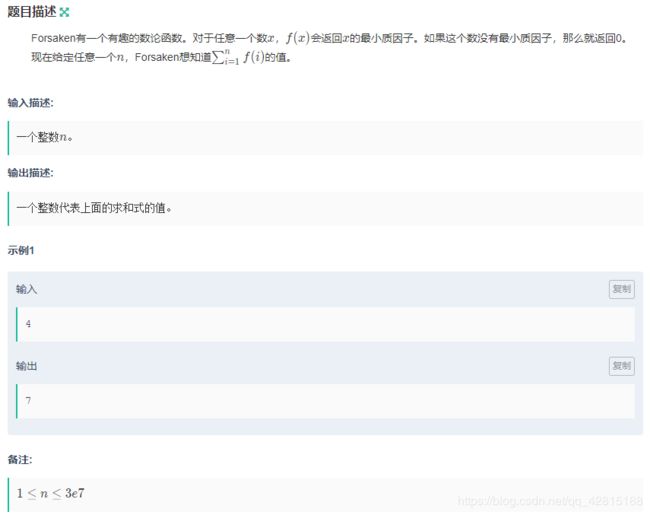
思路：线性筛法可以求 $1$ 到 $n$ 每个数字的最小质因子。

#include
#include
#include
#include

using namespace std;
typedef long long ll;
const int N = 3e7 + 10;

int p[N], tot;			// p存放所有素数
bool st[N];				// st判断当前数是否被筛掉

int main()
{
	int n;
	scanf("%d", &n);
	
	ll ans = 0;
	for(int i = 2; i <= n; i++)
	{
		if(!st[i])
		{
			p[tot++] = i;
			ans += i;				// 如果一个数本身是质数，最小质因子就是它本身
		}
		for(int j = 0; j < tot && i * p[j] <= n; j++)
		{
			st[i * p[j]] = true;
			ans += p[j];			// 对于像i*p[j]这样不是质数的数字，那么p[j]正好是他的最小质因子
			if(i % p[j] == 0)	break;
		}
	}
	
	printf("%lld\n", ans);
	
	return 0;
}

POJ 2262 Goldbach Conjecture

题目链接：点击这里

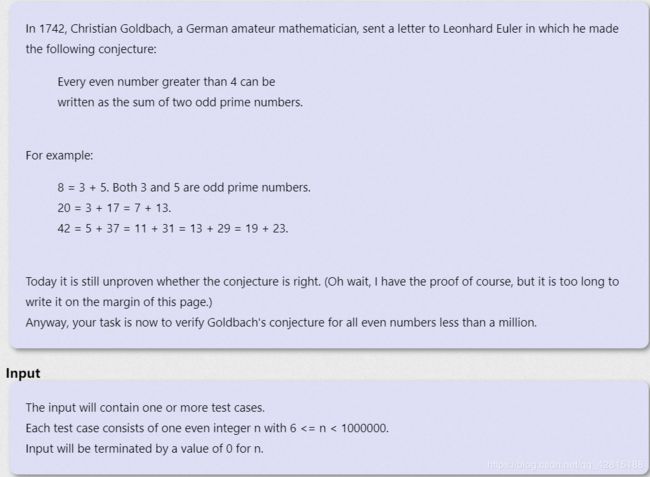
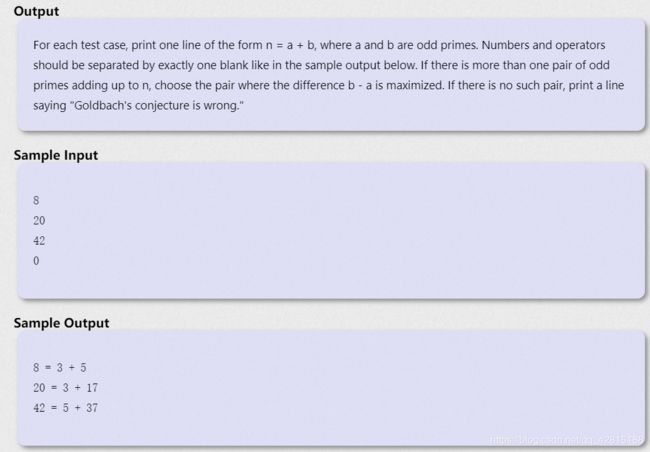
题意：

哥德巴赫猜想的内容如下：任意一个大于 $4$ 的偶数都可以拆成两个奇素数之和。

现在，你的任务是验证所有小于一百万的偶数能否满足哥德巴赫猜想。

思路：

除了 $2$之外，所有的质数都是奇数。哥德巴赫猜想目前没有反例。

AC代码：

#include
#include
#include
#include

using namespace std;
const int N = 1e6 + 10;

int n;
int primes[N], cnt;
bool st[N];

void get_primes(int n)
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i])  primes[cnt++] = i;
        for(int j = 0; primes[j] <= n / i; j++)
        {
            st[primes[j] * i] = true;
            if(i % primes[j] == 0)  break;
        }
    }
}

int main()
{
    get_primes(N - 1);
    
    while(~scanf("%d", &n), n)
    {
        for(int i = 1; ; i++)
        {
            int a = primes[i];
            int b = n - a;
            if(!st[b])
            {
                printf("%d = %d + %d\n", n, a, b);
                break;
            }
        }
    }
    
    return 0;
}

Codeforces B. Sherlock and his girlfriend（思维）

题目链接：点击这里

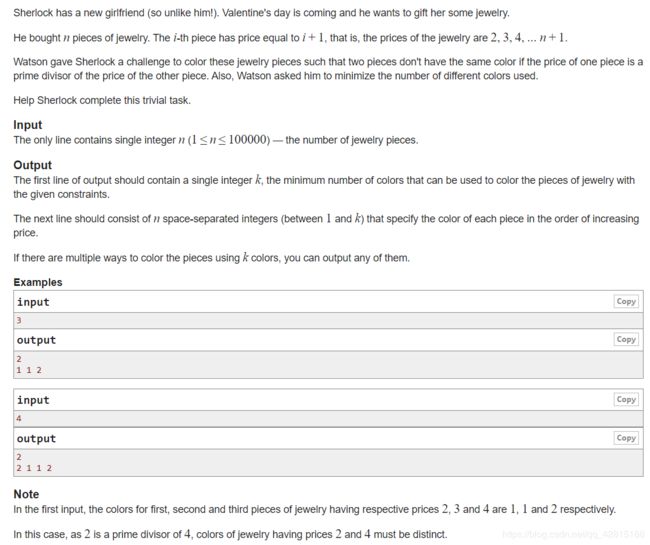
题意：$n$ 件珠宝，第 $i$ 件的价值是 $i+1$。给这些珠宝染色，使得一件珠宝的价格是另一件珠宝的价格的质因子时，两件珠宝的颜色不同。并且要求使用的颜色数尽可能少。

思路：所有的边一定是从一个质数指向一个合数。二分图。

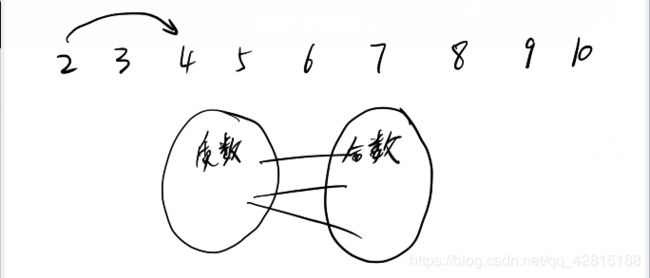
AC代码：

#include 
#include 
#include 
#include 

using namespace std;

const int N = 100010;

int primes[N], cnt;
bool st[N];

void init(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] * i <= n; j ++ )
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int main()
{
    int n;
    cin >> n;

    init(n + 1);

    if (n <= 2) puts("1");
    else puts("2");

    for (int i = 2; i <= n + 1; i ++ )
    {
        if (!st[i]) printf("1 ");
        else printf("2 ");
    }

    return 0;
}

POJ 2689 Prime Distance（二次筛法）

题目链接：点击这里

思路：

$L,R$ $(2147483647=2^{31}-1)$ 的范围很大，任何已知算法都无法在规定时间内生成 $[1,R]$ 中的所有质数。

但是 $R-L$ 的值很小，并且任何一个合数 $n$ 必定包含一个不超过 $n$ 的质因子。

所以，我们只需要用筛法求出 $2\sim \sqrt{R}$ 之间的所有质数。对于每个质数 $p$，把 $[L,R]$ 中能被 $p$ 整除的数标记，最终所有未被标记的数就是 $[L,R]$ 中的质数。对相邻的质数两两比较，找出差最大的即可。

用小区间里的质数 $p$ 去筛大区间 $[L,R]$，如何找到大于等于 $L$ 的最小的 $p$ 的倍数？

$\lceil \frac{L}{p}\rceil =\lfloor \frac{L+p-1}{p}\rfloor$

$\lceil \frac{L}{p}\rceil \times p=\lfloor \frac{L+p-1}{p}\rfloor \times p$

故 $P_0=max(2p,\frac{L+p-1}{p}\times p)$

AC代码：

#include
#include
#include
#include

using namespace std;
typedef long long ll;
const int N = 1000010;

int primes[N], cnt;
bool st[N];

int prime[N], tot;
bool vis[N];

void get_primes(int n)
{
    for(int i = 2; i <= n; i++)
    {
        if(!st[i])  primes[cnt++] = i;
        for(int j = 0; primes[j] * i <= n; j++)
        {
            st[i * primes[j]] = true;
            if(i % primes[j] == 0)  break;
        }
    }
}

int main()
{
    get_primes(50000);
    
    int l, r;
    while(cin >> l >> r)
    {
        memset(vis, 0, sizeof vis);
        tot = 0;
        
        for(int i = 0; i < cnt; i++)                // 用小区间筛大区间
        {
            ll p = primes[i];
            for(ll j = max(p * 2, (l + p - 1) / p * p); j <= r; j += p)
                vis[j - l] = true;                  // 用偏移量记录
        }
        
        for(int i = 0; i <= r - l; i++)             // 统计大区间里所有的质数
            if(!vis[i] && i + l >= 2)
                prime[tot++] = i + l;

        if(tot < 2)
        {
            puts("There are no adjacent primes.");
        }
        else
        {
            int minp = 0, maxp = 0;
            for(int i = 0; i + 1 < tot; i++)
            {
                int d = prime[i + 1] - prime[i];
                if(d < prime[minp + 1] - prime[minp])   minp = i;
                if(d > prime[maxp + 1] - prime[maxp])   maxp = i;
            }

            printf("%d,%d are closest, %d,%d are most distant.\n",
                prime[minp], prime[minp + 1],
                prime[maxp], prime[maxp + 1]);
        }
    }

    return 0;
}