JAVA代码—算法基础:0-1背包问题的回溯算法设计(续)
0-1背包问题的回溯算法设计(续)
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
0-1背包问题的回溯算法设计
问题描述:有N件物品和一个容量为V的背包。第i件物品的重量是w[i],价值是v[i]。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
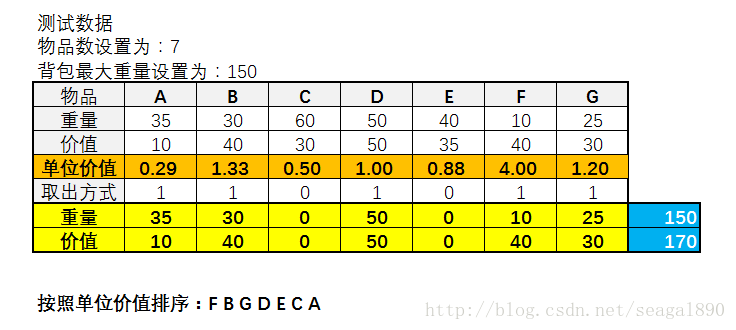
例如样例数据:
按照物品单位价值从大到小依次排列这 7 个物品为:F B G D E C A 。
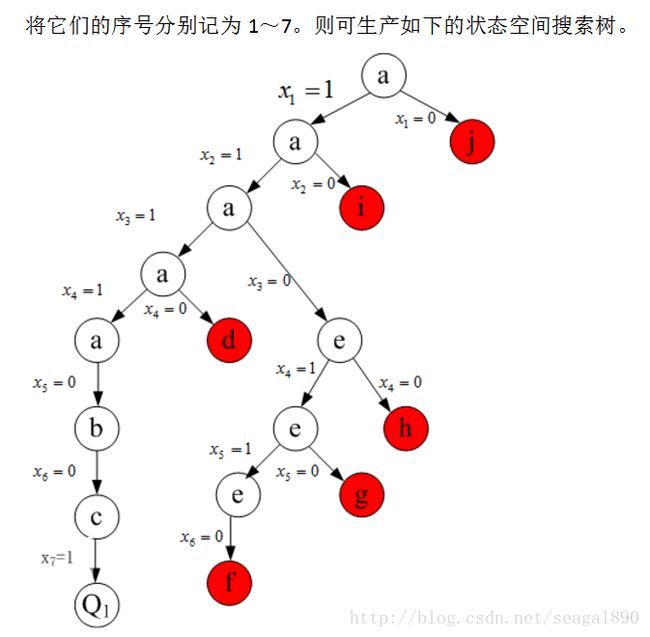
将它们的序号分别记为1~7。则可生产如下的状态空间搜索树。
其中各个节点处的限界函数值通过如下方式求得:
a. 40+40+30+50+35×(150-115)/40=190.625 (1,1,1,1,7/8,0,0)
b. 40+40+30+50+30×(150-115)/60=177.5 (1,1,1,1,0,7/12,0)
c.40+40+30+50+10×(150-115)/35=170 (1,1,1,1,0,0,1)
d. 40+40+30+35+30×(150-105)/60=167.5 (1,1,1,0,1,3/4,0)
e. 40+40+50+35+30×(150-130)/60=175 (1,1,0,1,1,1/3,0)
f. 40+40+50+35+10×(150-130)/35=170.71 (1,1,0,1,1,0,4/7)
g. 40+40+50+30=160 (1,1,0,1,0,1,0)
h. 40+40+35+30+10×(150-140)/35=146.85 (1,1,0,0,1,1,2/7)
i. 40+30+50+35+30×(150-125)/60=167.5 (1,0,1,1,1,5/12,0)
j. 40+30+50+35+30×(150-145)/60=157.5 (0,1,1,1,1,1/12,0)
在Q1处获得该问题的最优解为 ,背包效益为170。
即在背包中装入物品F、B、G、D、A时达到最大效益,为170,重量为150。
0-1背包问题回溯算法设计——求解问题
设定基础数据
//物品数量
int n=7;
//背包容量
int capacity=150;
//物品重量数组
double weight[]= {35,30, 60, 50, 40, 10, 25};
//物品价值数组
double value[]= {10, 40, 30, 50, 35, 40, 30};
//最大价值
int maxValue = 0;
//当前最大价值
int currentValue;
//当前重量
int currentWeight;
// 装入方法数组
int[] way = new int[n];
//最佳装入方法数组
int[] bestWay = new int[n];算法设计
/*
* 回溯算法设计
* */
public void backTrack(int t) {
// 已经搜索到根节点
if (t > n - 1) {
if (currentValue > maxValue) {
maxValue = currentValue;
for (int i = 0; i < n; i++)
bestWay[i] = way[i];
}
return;
}
// 搜索左边节点
if (currentWeight + weight[t] <= capacity) {
currentWeight += weight[t];
currentValue += value[t];
way[t] = 1;
//回溯
backTrack(t + 1);
currentWeight -= weight[t];
currentValue -= value[t];
way[t] = 0;
}
// 不装入这个物品,直接搜索右边的节点
if (bound(t + 1) >= maxValue) {
backTrack(t + 1);
}
}
// 用于计算剩余物品的最高价值上界
public double bound(int k) {
double maxLeft = currentValue;
int leftWeight = capacity - currentWeight;
// 尽力依照单位重量价值次序装剩余的物品
while (k <= n - 1 && leftWeight > weight[k]) {
leftWeight -= weight[k];
maxLeft += value[k];
k++;
}
// 不能装时,用下一个物品的单位重量价值折算到剩余空间。
if (k <= n - 1) {
maxLeft += value[k] / weight[k] * leftWeight;
}
return maxLeft;
}完整代码
package com.bean.knapsack2;
import com.bean.bagalgorithm.Bag;
/*
* 用回溯法实现0-1背包问题。
* 在回溯开始之前,首先对于背包中的物品按照单位重量价值进行排序,方便于后面右子树的剪枝操作。
* 在初始化物品的重量和价值时,已经按照单位重量的价值排好了序。
* 一个典型的子集树问题,对于背包中的每一个物品,可以选择放入(左子树)或者不放入(右子树)。
* 依次对每个节点进行搜索,得到最优解。
* */
public class Knapsack2 {
/*
* 物品 A B C D E F G
* 重量 35 30 60 50 40 10 25
* 价值 10 40 30 50 35 40 30
*
* */
*
//物品数量
int n=7;
//背包容量
int capacity=150;
//物品重量数组
double weight[]= {35,30, 60, 50, 40, 10, 25};
//物品价值数组
double value[]= {10, 40, 30, 50, 35, 40, 30};
//最大价值
int maxValue = 0;
//当前最大价值
int currentValue;
//当前重量
int currentWeight;
// 装入方法数组
int[] way = new int[n];
//最佳装入方法数组
int[] bestWay = new int[n];
/*
* 回溯算法设计
* */
public void backTrack(int t) {
// 已经搜索到根节点
if (t > n - 1) {
if (currentValue > maxValue) {
maxValue = currentValue;
for (int i = 0; i < n; i++)
bestWay[i] = way[i];
}
return;
}
// 搜索左边节点
if (currentWeight + weight[t] <= capacity) {
currentWeight += weight[t];
currentValue += value[t];
way[t] = 1;
//回溯
backTrack(t + 1);
currentWeight -= weight[t];
currentValue -= value[t];
way[t] = 0;
}
// 不装入这个物品,直接搜索右边的节点
if (bound(t + 1) >= maxValue) {
backTrack(t + 1);
}
}
// 用于计算剩余物品的最高价值上界
public double bound(int k) {
double maxLeft = currentValue;
int leftWeight = capacity - currentWeight;
// 尽力依照单位重量价值次序装剩余的物品
while (k <= n - 1 && leftWeight > weight[k]) {
leftWeight -= weight[k];
maxLeft += value[k];
k++;
}
// 不能装时,用下一个物品的单位重量价值折算到剩余空间。
if (k <= n - 1) {
maxLeft += value[k] / weight[k] * leftWeight;
}
return maxLeft;
}
public static void main(String[] args) {
Knapsack2 knspsack2 = new Knapsack2();
knspsack2.backTrack(0);
System.out.println("该背包能够取到的最大价值为:" + knspsack2.maxValue);
System.out.println("当前背包的重量为:" + knspsack2.capacity);
System.out.println("物品的取出方法为取出的方法为:");
for (int i : knspsack2.bestWay)
System.out.print(i + " ");
}
}
运行结果:
该背包能够取到的最大价值为:170
当前背包的重量为:150
物品的取出方法为取出的方法为:
1 1 0 1 0 1 1
(完)
附加信息:
回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中,按照深度优先的策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时,总是先判断该结点是否肯定不包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的系统搜索,逐层向其祖先结点回溯。否则,进入该子树,继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时,要回溯到根,且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时,只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法,它适用于解一些组合数较大的问题。
回溯算法也叫试探法,它是一种系统地搜索问题的解的方法。
用回溯算法解决问题的一般步骤:
1、 针对所给问题,定义问题的解空间,它至少包含问题的一个(最优)解。
2 、确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
3 、以深度优先的方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索。
确定了解空间的组织结构后,回溯法就从开始结点(根结点)出发,以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点,同时也成为当前的扩展结点。在当前的扩展结点处,搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点,并成为当前扩展结点。如果在当前的扩展结点处不能再向纵深方向移动,则当前扩展结点就成为死结点。此时,应往回移动(回溯)至最近的一个活结点处,并使这个活结点成为当前的扩展结点。回溯法即以这种工作方式递归地在解空间中搜索,直至找到所要求的解或解空间中已没有活结点时为止。