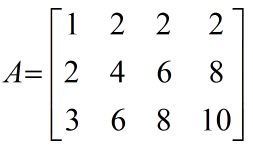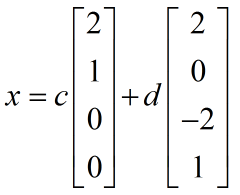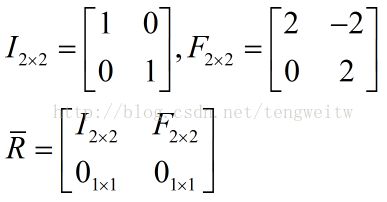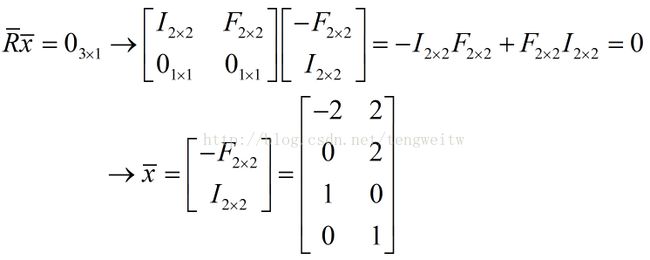【线性代数】矩阵的零空间

矩阵A的零空间就Ax=0的解的集合。

零空间的求法：对矩阵A进行消元求得主变量和自由变量；给自由变量赋值得到特解；对特解进行线性组合得到零空间。

假设矩阵如下：

对矩阵A进行高斯消元得到上三角矩阵U，继续化简得到最简矩阵R：

由于方程Ax=0的右侧是零向量，所以只对矩阵A进行消元不会影响解,因此不需要增广矩阵，所以有：

从上面的高斯消元的结果可以看出，矩阵A的秩为2，其中第1，3列为主元列，2，4列为自由列，对应于方程主来说，形式转变如下：

从上式可以看出，x2,x4是自由变量，我们可以随意赋值，x2=0,x4=1；x2=1,x4=0可以分别得到两个特解（几个自由变量就有几个特解）：

然后我们将两组特解进行线性组合就得到了矩阵A的零空间：

上面我们从数值解的角度描述了矩阵零空间的求法，下面从公式角度分析：

上面我们经过消元（ 行变换，不改变行空间和零空间，只改变列空间）得到了最简形式R。我们将R经过列变换得到如下矩阵：

我们可以对方程式作如下变形：

我们之所以进行上述变换，是为了有更好的表示形式（不进行列变换也行，但是要记住哪一列是单位矩阵I中的，哪一列是自由变量矩阵F中的）：

这样我们代入方程式可以得到零空间矩阵：

从上面的推导可以看出，得到的零空间矩阵的每一列就是我们前面的特解(注意要变换顺序！交换第2，3行,结果便和前面相同)。因此，我们可以从通过消元法得到最简式R，然后就可以直接得到零空间矩阵，则 零空间就是零空间矩阵各列向量的线性组合，而不需要像前面那样先给x2,x4赋值，然后回代到方程中得到两个特解，从而得到矩阵的零空间。

下面再举一例：

由于R本来就具有很好的形式，就不用进行列变换了：

于是通过解方程得到零空间矩阵：

注：最简矩阵R和零空间矩阵x在MATLAB中可以分别用命令rref(A)，null(A,'r')得到

原文：http://blog.csdn.net/tengweitw/article/details/40039373

作者：nineheadedbird