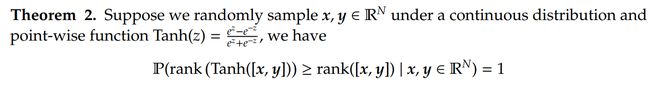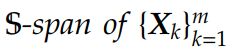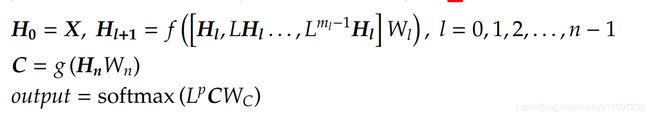顶破天花板的图卷积结构：Break the Ceiling: Stronger Multi-scale Deep Graph Convolutional Networks

Break the Ceiling: Stronger Multi-scale Deep Graph Convolutional Networks（地基打得好，突破上限不会倒）

闲来无事，找篇论文粗读一下：

Break the Ceiling: Stronger Multi-scale Deep Graph Convolutional Networks。

初看题目Break the Ceiling，透露些许傲骄，初扫论文感觉模型数学包装很好，结果也提升比较多，大家可以抛开论文的切入点，横向对比一下网络结构（比如CNN的denseNet, Inception Net）也许你能找到些思想来源。网络模型比较简单，想仔细了解的看代码：

https://github.com/PwnerHarry/Stronger_GCN

1、分析现有的GNN由于激活函数和结构受限的局限性；

2、将基于谱的图卷积和深度GCN网络推广到了块Krylov空间形式，在该空间下设计了两个结构。两者利用了不同的多尺度信息，并解释了在一定的条件下，两种体系结构是等价的。。

3、节点分类性能好。（到底有没有顶破天花板呢，继续看。）

说起GCN这个东西也不新鲜，况且某综述paper有把它捧的很高。近年来的确比较火。不管是黑猫白猫抓到老鼠就是好猫，GCN在非欧数据上确实表现出了优越的性能，比如点云、社会关系等等吧。

一、顶破天花板那肯定需要解决了目前方法固有的问题：

层数少，模型浅，表达能力不足。那目前的方法为啥不能扩展到更深或者像CNN一样花里胡哨的结构上呢。作者借用解释如下：

1. 图卷积可以看做是Laplacian 平滑的一种特殊形式，更多层容易就是更多的平滑，以至于每个节点都被“盘”的差不多了，再具有可分性的节点也都变成了“鹅卵石”了，更难以区分。
2. 大多情况，标签信息不需要遍历整个图；还有通过多尺度粗化（采样）就能得到和deeper相同的embedding。那么为啥还要增加参数量和训练难度呢！

注意到这篇文章的小伙伴，想必基于谱的图卷积定义和说明这部分已经看过N次了，咱直接跳过。

为啥不能扩展？

（a）

是学习的特征。

这也就是说，更深的层编码更多图结构的静态信息，丢失所有节点特征的信息。

（a）

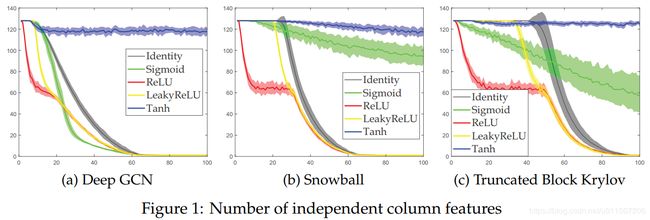
这说明Tanh较好地保持了列特征之间的线性无关性。效果看下图：

二、Spectral Graph Convolution and Block Krylov Subspace Methods

这里先说一下如何定义块Krylov 子空间

表示block vector subspace。

在该空间下定义一个内积要满足：

1 线性的：也就是

2 具有对称性：

3 具有确定性：X是满秩的，就必须是确定，有且仅当X=0时，。

本文定义如下：

该空间下的跨度定义为：

因此，关于A B S 的 m阶块Krylov 子空间定义为：

对应的块K矩阵为：

三、块Krylov子空间形式的谱图卷积：

任何谱图卷积的谱滤波器可以写成块Krylov矩阵和一个可学习的参数矩阵乘积的形式。这部分比较长，但是不难，贴上原文：

卷积已经定义好了，那么深度GCN就可表示为：

其中h 是非线性激活函数；隐层特征表示为：

 

四、计算

如何计算的正交基和确定m呢，困难在于：

1、 H_i是变化的，m_i就变成一个变量，需要根据参数矩阵自适应改变。

2、 block Arnoldi 算法需要矩阵的QR分解，那么在反向传播中这点就无法实现。

话说有困难就解决，不能直接解就放弃，换个思路：多尺度方法。

1、“滚雪球”结构

2、“被削的Krylov”结构

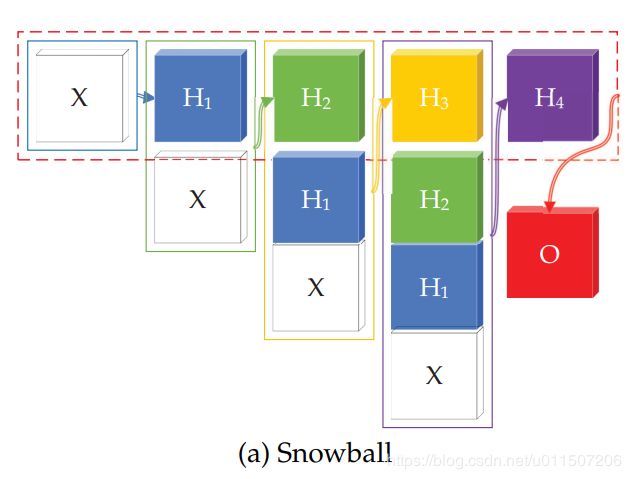
“滚雪球”结构：

这个名字很形象，就是所到之处寸雪不留，就是每一层将前面所有层的特征都加进去，看这个结构是不是就有了类似CNN密集连接的味道了：

结构图

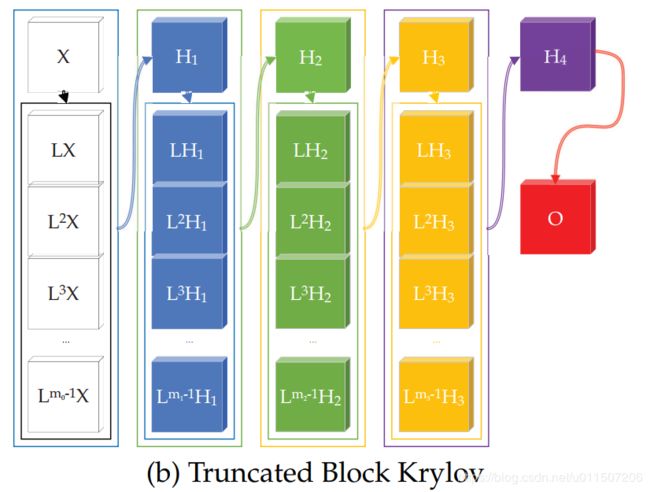
Truncated Krylov中把m_i当做超参数来解：因此一个截断的块Krylov 网络表示为：

这个m,如果是每层设置一个参数 超参特太多了，一个m能不能使得所有的层都满足：

显然不能够，那就只能去近似它了，显然误差也无法确定。也只能实验选个m, trade-off一下性能和计算量吧。

至此，我也简要理解一下本文关于多尺度背后的思考：

更多层的传统的GCN变成了节点和其n-hop的加权平均（不考虑非线性）。随着范围扩大，相同连接组件中的节点往往具有相同的(全局)特性，从而失去了他们的特有的特征信息，这使得节点特征是不可区分的。因此，为了获得可区分的信息，我们必须将底层的特征也拼接上去，那么就是所谓的“雪球”结构，另外一个结构也是每层都是从第L0开始连接，因此每个节点的局部信息不会被稀释在每一层。这就能够保证在更深结构中保持节点特有的信息。

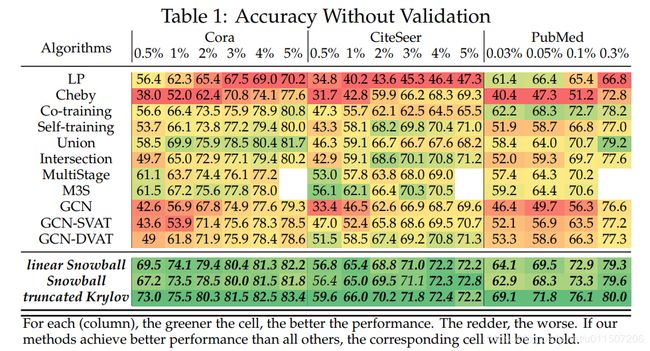
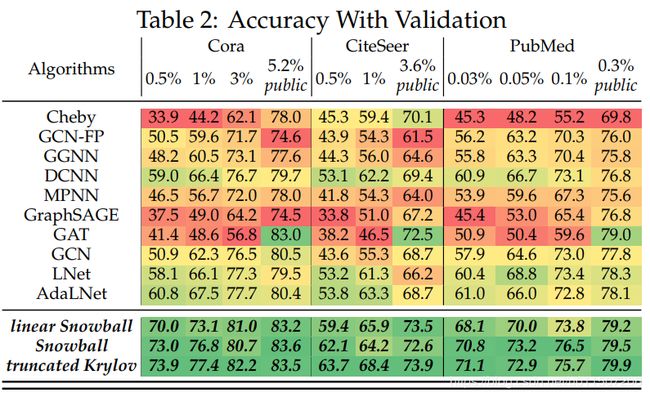
五、实验结果

效果真的不错，算不算突破上限，顶破天花板呢，自己考量吧，具体实验细节没有看。