宾夕法尼亚大学Coursera运动规划公开课学习有感

元宵节过去啦, 新的学期开始了.
前一段时间学习了Coursera上的公开课: Computational Motion Planning, 这是VJKumar教授Robotics系列课程的其中一个. 这一部分, 顾名思义, 就是讲运动规划的. 这套课程并不是很深刻, 但是它的各算法的衔接非常流畅, 每个算法的引出非常自然. 对于我自己, 通过看论文, 每个算法虽然都见过, 但是自己总结的不够系统, 上过这个公开课就好很多.
感觉这套课程质量很高, 课堂讨论区很活跃, 来自全世界的各路大神都分享自己做作业的感受. 很多东西自己想是绝对想不到的. 作业做完, 感受更加深刻, 对于算法的理解以及算法细节部分实现也有了新的认识, 下面还是把自己的一点小小的感悟写在下面吧. 这一篇文章讲的都是graph-based planning，个人理解是把所有可以走的路线看成节点的路径规划。

Introduction to Computational Motion Planning

介绍，路径规划是什么。下面有一些英文术语: G/V/E: 一个图G(Graph)，由顶点V(Vertices)和连线E（Edge）构成。连线把所有顶点连接起来。连线通常用数值标记，表示相关的量例如距离或者消耗。通常来讲，目标都是从起始位置到终点位置路程最短。

Grassfire Algorithm

这个算法，可以从目标开始，绕着相邻的格子标数字。伪代码如图:

从任意一个格子出发，只需要寻找格子周边数字最小的格子，走过去就行。像下面这种一圈都是9的，那任意一个格子都可以了。

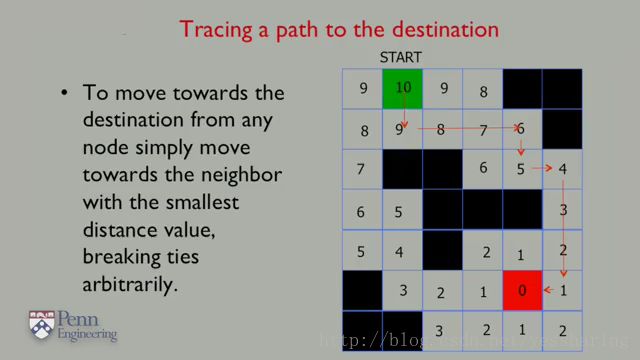
如果在标记格子的过程中，起始位置还没有被标记到数字，标记的过程就结束了。那就说明无法从起始位置到达目标。

关于计算效率，挺低的。这个算法和格子数目成正比。如果维数很大，那这个格子数目就会巨大。（格子数目和维数成指数关系）

Dijkstra算法（此处指适用于2D的算法)

伪代码如图，每个节点都有两个属性，一个是父节点，一个是距离。寻找每个节点的相邻节点中有标记距离最小的那个点，这个点就是下一个节点。反复迭代。

算法效率：这里提到了a clever data structure叫做priority queue, 可以使维数增加的时候, 计算效率不会迅速较低. 这个priority queue, 优先级队列, 感觉应该是数据结构里面的内容?这个有待向学计算机的同学考证.

A*算法:(此处指适用于2D的算法)

上面讲的都是效率比较低的，因为是全向搜索。A*算法效率比较高，因为使用启发式算法会慢慢往目标方向上靠近，而不是全方向都在搜索。

这是伪代码。g是current节点和起点的距离， f是节点g值以及这个节点的启发式成本。上一页说，启发式成本函数有如下特点：在目标处启发式成本函数值为0，对于相邻的两个节点x和y，应该满足 h(x)<h(y)+d(x,y) .常见的启发式成本函数h包括从节点到目标的距离(直线距离)，从节点到目标横坐标差和纵坐标差的和。每次循环都要寻找f最小的，当作下一次循环的起点值（就是设置成current，寻找它相邻的节点，再循环）

和dijkstra算法相比，快了很多呢。

---

附录:
来自维基百科的A*伪代码：

function A*(start, goal)
    // The set of nodes already evaluated.
    closedSet := {}
    // The set of currently discovered nodes still to be evaluated.
    // Initially, only the start node is known.
    openSet := {start}
    // For each node, which node it can most efficiently be reached from.
    // If a node can be reached from many nodes, cameFrom will eventually contain the
    // most efficient previous step.
    cameFrom := the empty map
// For each node, the cost of getting from the start node to that node.
    gScore := map with default value of Infinity
    // The cost of going from start to start is zero.
    gScore[start] := 0 
    // For each node, the total cost of getting from the start node to the goal
    // by passing by that node. That value is partly known, partly heuristic.
    fScore := map with default value of Infinity
    // For the first node, that value is completely heuristic.
    fScore[start] := heuristic_cost_estimate(start, goal)
while openSet is not empty
        current := the node in openSet having the lowest fScore[] value
        if current = goal
            return reconstruct_path(cameFrom, current)
        openSet.Remove(current)
        closedSet.Add(current)
        for each neighbor of current
            if neighbor in closedSet
                continue        // Ignore the neighbor which is already evaluated.
            // The distance from start to a neighbor
            tentative_gScore := gScore[current] + dist_between(current, neighbor)
            if neighbor not in openSet  // Discover a new node
                openSet.Add(neighbor)
            else if tentative_gScore >= gScore[neighbor]
                continue        // This is not a better path.
// This path is the best until now. Record it!
            cameFrom[neighbor] := current
            gScore[neighbor] := tentative_gScore
            fScore[neighbor] := gScore[neighbor] + heuristic_cost_estimate(neighbor, goal)
return failure
function reconstruct_path(cameFrom, current)
    total_path := [current]
    while current in cameFrom.Keys:
        current := cameFrom[current]
        total_path.append(current)
    return total_path