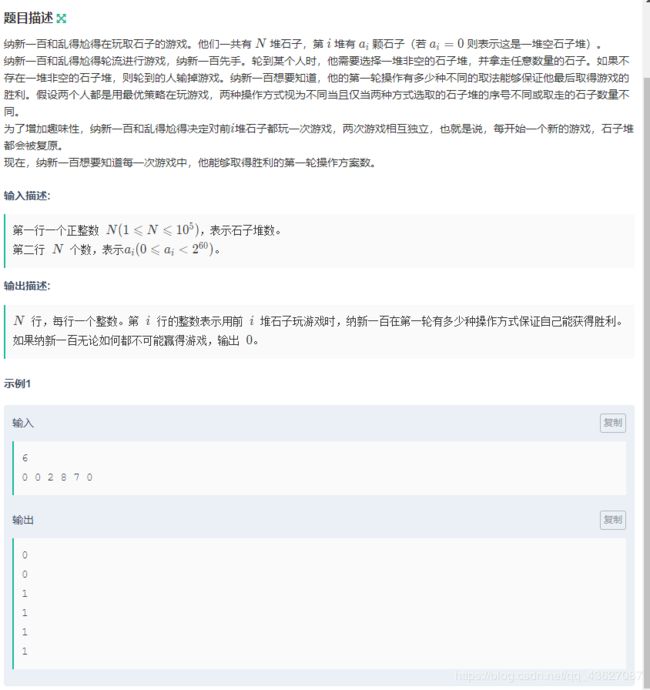
2020 CCPC Wannafly Winter Camp Day2 C 纳新一百的石子游戏（博弈论）

题意：

有 $n$ 堆石子，第 $i$ 堆石子有 $a_i$ 个。
两个人可以选择某些石子堆玩游戏：
两人交替进行操作，轮到某个人时需要选择一堆非空的石子并拿走一些。
若不存在一堆非空的石子，则轮到的人输。
对 $\forall i\in \left[1,N\right]$，求用前 $i$ 堆石子玩游戏时先手取石子有多少种取法必胜。

一个简单结论：
用前 $i$ 堆石子玩游戏时，若 $\underset{j=1}{\overset{i}{⨁}}{a}_i=0$ 则先手必败，反之先手必胜。

若先手必胜，设 $\underset{j=1}{\overset{i}{⨁}}{a}_i=k$，注意到一个的性质：

任意一个在 kk 的二进制最高位 $1$ 对应的位下为 $1$ 的 $a_i$ 都可以减少一些使得后手必败。
此时，方案数就是石子数在 $k$ 的二进制最高位 $1$ 对应的位下为 $1$ 的石子堆数，按位统计即可。

AC代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
#define sd(n) scanf("%d", &n)
#define sdd(n, m) scanf("%d%d", &n, &m)
#define sddd(n, m, k) scanf("%d%d%d", &n, &m, &k)
#define pd(n) printf("%d\n", n)
#define pc(n) printf("%c", n)
#define pdd(n, m) printf("%d %d\n", n, m)
#define pld(n) printf("%lld\n", n)
#define pldd(n, m) printf("%lld %lld\n", n, m)
#define sld(n) scanf("%lld", &n)
#define sldd(n, m) scanf("%lld%lld", &n, &m)
#define slddd(n, m, k) scanf("%lld%lld%lld", &n, &m, &k)
#define sf(n) scanf("%lf", &n)
#define sc(n) scanf("%c", &n)
#define sff(n, m) scanf("%lf%lf", &n, &m)
#define sfff(n, m, k) scanf("%lf%lf%lf", &n, &m, &k)
#define ss(str) scanf("%s", str)
#define rep(i, a, n) for (int i = a; i <= n; i++)
#define per(i, a, n) for (int i = n; i >= a; i--)
#define mem(a, n) memset(a, n, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define pb push_back
#define all(x) (x).begin(), (x).end()
#define fi first
#define se second
#define mod(x) ((x) % MOD)
#define gcd(a, b) __gcd(a, b)
#define lowbit(x) (x & -x)
typedef pair<int, int> PII;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int MOD = 1e9 + 7;
const double eps = 1e-9;
const ll INF = 0x3f3f3f3f3f3f3f3fll;
const int inf = 0x3f3f3f3f;
inline int read()
{
    int ret = 0, sgn = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            sgn = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        ret = ret * 10 + ch - '0';
        ch = getchar();
    }
    return ret * sgn;
}
inline void Out(int a)
{
    if (a > 9)
        Out(a / 10);
    putchar(a % 10 + '0');
}

ll gcd(ll a, ll b)
{
    return b == 0 ? a : gcd(b, a % b);
}

ll lcm(ll a, ll b)
{
    return a * b / gcd(a, b);
}
///快速幂m^k%mod
ll qpow(ll a, ll b, ll mod)
{
    if (a >= mod)
        a = a % mod + mod;
    ll ans = 1;
    while (b)
    {
        if (b & 1)
        {
            ans = ans * a;
            if (ans >= mod)
                ans = ans % mod + mod;
        }
        a *= a;
        if (a >= mod)
            a = a % mod + mod;
        b >>= 1;
    }
    return ans;
}

// 快速幂求逆元
int Fermat(int a, int p) //费马求a关于b的逆元
{
    return qpow(a, p - 2, p);
}

///扩展欧几里得
int exgcd(int a, int b, int &x, int &y)
{
    if (b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    int g = exgcd(b, a % b, x, y);
    int t = x;
    x = y;
    y = t - a / b * y;
    return g;
}

///使用ecgcd求a的逆元x
int mod_reverse(int a, int p)
{
    int d, x, y;
    d = exgcd(a, p, x, y);
    if (d == 1)
        return (x % p + p) % p;
    else
        return -1;
}

///中国剩余定理模板0
ll china(int a[], int b[], int n) //a[]为除数，b[]为余数
{
    int M = 1, y, x = 0;
    for (int i = 0; i < n; ++i) //算出它们累乘的结果
        M *= a[i];
    for (int i = 0; i < n; ++i)
    {
        int w = M / a[i];
        int tx = 0;
        int t = exgcd(w, a[i], tx, y); //计算逆元
        x = (x + w * (b[i] / t) * x) % M;
    }
    return (x + M) % M;
}

int n;
ll k, a;
int cnt[100];
int main()
{
    sd(n);
    k = 0;
    rep(i, 1, n)
    {
        sld(a);
        k ^= a;
        rep(j, 0, 59)
            cnt[j] += (a >> j) & 1;
        int j = 59;
        while (~j && !(k & (1ll << j)))
            j--;
        printf("%d\n", ~j ? cnt[j] : 0);
    }
    return 0;
}