贪心算法
目录
一.贪心算法的一些东西
1.思想
2.引例
3.贪心算法的基本要素
4.贪心算法的基本思路
5.贪心算法适用的问题
6.贪心算法实现框架
二.贪心实例
1.背包问题
2.最优装载问题
3.哈夫曼编码
4.单源最短路径
Dijkstra算法(会填写表)
5.最小生成树(会画出图)
①Prime Algorithm(按顶点)
②Kruskal Algorithm(按边)
6.完美字符串(就是统计出现次数最多的字符)
7.一个我取不出名的问题,叫‘删数问题’8
8.多机调度问题
9.数列极差问题
10.分马问题
11.取数游戏
12.整数分解然后计算最大乘积(这个怕不是作业)
13.顾客等待问题(这个怕不也是作业)
一.贪心算法的一些东西
1.思想
贪心算法(又称贪婪算法)是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,只做出的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑,它所作出的选择只是在某种意义上的局部最优选择。当然,希望贪心算法得到的最终结果也是整体最优的。
虽然贪心算法不能对所有问题都得到整体最优解,但对许多问题它能产生整体最优解。如单源最短路径问题,最小生成树问题等。在一些情况下,即使贪心算法不能得到整体最优解,其最终结果却是最优解的很好近似。
2.引例
①凑硬币
贪心法不一定能产生正确的答案。
例如,若引进一个1角1分的硬币,设从如下集合{1,1,2,2,2,5,10,10,11,11}中数出25分,按贪心法,共4个硬币。但最优解仅为3个硬币。
这说明贪心法得到的解只是一个可行解。
②过桥
夜晚过一桥,甲过需要一分钟,乙两分钟,丙五分钟,丁十分钟。桥一次最多只能承受两人,过桥必须使用手电筒,现在只有一只手电筒。请问4人最少用多少时间全部过桥?
最优解:17min 贪心算法:19min
③活动安排问题
问题描述
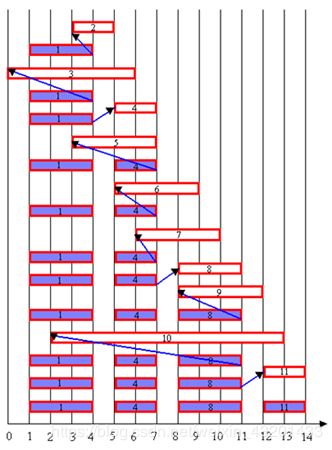
活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合,是可以用贪心算法有效求解的很好例子。该问题要求高效地安排一系列争用某一公共资源的活动。贪心算法提供了一个简单、漂亮的方法使得尽可能多的活动能兼容地使用公共资源。
问题分析
设有n个活动的集合E={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si
由于输入的活动以其完成时间的非减序排列,所以算法greedySelector每次总是选择具有最早完成时间的相容活动加入集合A中。该算法的贪心选择的意义是使剩余的可安排时间段极大化,以便安排尽可能多的相容活动。
算法greedySelector的效率极高。当输入的活动已按结束时间的非减序排列,算法只需O(n)的时间安排n个活动,使最多的活动能相容地使用公共资源。如果所给出的活动未按非减序排列,可以用O(nlogn)的时间重排。
举例:设待安排的11个活动的开始时间和结束时间按结束时间的非减序排列如下表:
| i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| s[i] |
1 |
3 |
0 |
5 |
3 |
5 |
6 |
8 |
8 |
2 |
12 |
| f[j] |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
若被检查的活动i的开始时间Si小于最近选择的活动j的结束时间fi,则不选择活动i,否则选择活动i加入集合A中。
贪心算法并不总能求得问题的整体最优解。但对于活动安排问题,贪心算法greedySelector却总能求得的整体最优解,即它最终所确定的相容活动集合A的规模最大。这个结论可以用数学归纳法证明。
int greedyselector(int []s,int []f,bool a[])
{
int n = s.length(),j = 1,i,count = 1;
a[1] = true;
for(i = 2;i <= n;i++)
{
if(s[i] > f[j])
{
a[i] = true;
j = i;
count++;
}
else
a[i] = false;
}
return count;
}3.贪心算法的基本要素
①贪心选择性质
②最优子结构性质
4.贪心算法的基本思路
①建立数学模型来描述问题;
②把求解的问题分成若干个子问题;
③对每一子问题求解,得到子问题的局部最优解;
④把子问题的局部最优解合成原来问题的一个解。
5.贪心算法适用的问题
贪心策略适用的前提是:局部最优策略能导致产生全局最优解。实际上,贪心算法适用的情况很少。一般,对一个问题分析是否适用于贪心算法,可以先选择该问题下的几个实际数据进行分析,就可做出判断。
6.贪心算法实现框架
Greedy(C){
s={};
while (not solution(S)){ //集合S没有构成问题的一个解
x=select(C); //在候选集合中做出贪心选择
if constraint(S,x) //判断集合S中加入x后的解是否可行
s=s+{x};
C=C-{x};
}
return s;
}
二.贪心实例
1.背包问题
①0-1背包(不能用贪心!!!)
问题描述
给定n种物品和一个背包。物品i的重量是Wi,其价值为Vi,背包的容量为C。应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
在选择装入背包的物品时,对每种物品i只有2种选择(0或1,所以叫0-1背包问题),即装入背包或不装入背包。不能将物品i装入背包多次,也不能只装入部分的物品i。
②背包
问题描述
与0-1背包问题类似,所不同的是在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包,1≤i≤n。
这2类问题都具有最优子结构性质,极为相似,但背包问题可以用贪心算法求解,而0-1背包问题却不能用贪心算法求解。
问题分析
首先计算每种物品单位重量的价值Vi/Wi,然后,依贪心选择策略,将尽可能多的单位重量价值最高的物品装入背包。若将这种物品全部装入背包后,背包内的物品总重量未超过C,则选择单位重量价值次高的物品并尽可能多地装入背包。依此策略一直地进行下去,直到背包装满为止。
对于0-1背包问题,贪心算法之所以不能得到最优解是因为在这种情况下,它无法保证最终能将背包装满,部分闲置的背包空间使每公斤背包空间的价值降低了。事实上,在考虑0-1背包问题时,应比较选择该物品和不选择该物品所导致的最终方案,然后再作出最好选择。由此就导出许多互相重叠的子问题。该类问题可采用动态规划算法。
void knapsack(int n,float m,float v[],float w[],float x[])
{
sort(n,v,w);
float c = m;
for(int i = 1;i <= n;i++)
x[i] = 0;
for(int i = 1;i <= n;i++)
{
if(w[i] > c)
break;
x[i] = 1;
c -= w[i];
}
if(i <= n)
x[i] = c/w[i];
}2.最优装载问题
问题描述
有一批集装箱要装上一艘载重量为c的轮船。其中集装箱i的重量为Wi。最优装载问题要求确定在装载体积不受限制的情况下,将尽可能多的集装箱装上轮船
问题分析
void load(int x[],int w[],int n,int c)
{
int *t = new int[n + 1];
sort(w,t,n);
for(int i = 1;i <= n;i++)
x[i] = 0;
for(int i = 1;i <= n && w[t[i]] <= c;i++)
{
x[t[i]] = 1;
c -= w[t[i]];
}
}3.哈夫曼编码
会画出树,时间复杂度为O(n^2)
4.单源最短路径
Dijkstra算法(会填写表)
算法步骤
设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到所有其他顶点之间的最短路径长度。
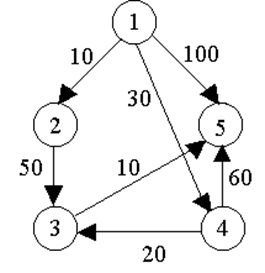
例题1
| 迭代 |
S |
V2 |
V3 |
V4 |
V5 |
| 初始 |
{1} |
10 |
∞ |
30 |
100 |
| 1 |
{1,2} |
10 |
60 |
30 |
100 |
| 2 |
{1,2,4} |
10 |
50 |
30 |
90 |
| 3 |
{1,2,4,3} |
10 |
50 |
30 |
60 |
| 4 |
{1,2,4,3,5} |
10 |
50 |
30 |
60 |
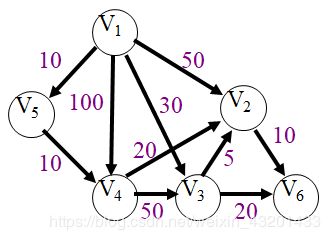
例题2
| 迭代 |
S |
V2 |
V3 |
V4 |
V5 |
V6 |
| 初始 |
{1} |
50 |
30 |
100 |
10 |
∞ |
| 1 |
{1,5} |
50 |
30 |
20 |
10 |
∞ |
| 2 |
{1,5,4} |
40 |
30 |
20 |
10 |
∞ |
| 3 |
{1,5,4,3} |
35 |
30 |
20 |
10 |
50 |
| 4 |
{1,5,4,3,2} |
35 |
30 |
20 |
10 |
45 |
| 5 |
{1,5,4,3,2,6} |
35 |
30 |
20 |
10 |
45 |
5.最小生成树(会画出图)
设G =(V,E)是无向连通带权图,即一个网络。E中每条边(v,w)的权为c[v][w]。如果G的子图G’是一棵包含G的所有顶点的树,则称G’为G的生成树。生成树上各边权的总和称为该生成树的耗费。在G的所有生成树中,耗费最小的生成树称为G的最小生成树。
网络的最小生成树在实际中有广泛应用。例如,在设计通信网络时,用图的顶点表示城市,用边(v,w)的权c[v][w]表示建立城市v和城市w之间的通信线路所需的费用,则最小生成树就给出了建立通信网络的最经济的方案。
用贪心算法设计策略可以设计出构造最小生成树的有效算法。本节介绍的构造最小生成树的Prim算法和Kruskal算法都可以看作是应用贪心算法设计策略的例子。尽管这2个算法做贪心选择的方式不同,它们都利用了下面的最小生成树性质:
设G=(V,E)是连通带权图,U是V的真子集。如果(u,v)∈E,且u ∈ U,v ∈ V-U,且在所有这样的边中,(u,v)的权c[u][v]最小,那么一定存在G的一棵最小生成树,它以(u,v)为其中一条边。这个性质有时也称为MST(Most Small Tree)性质。
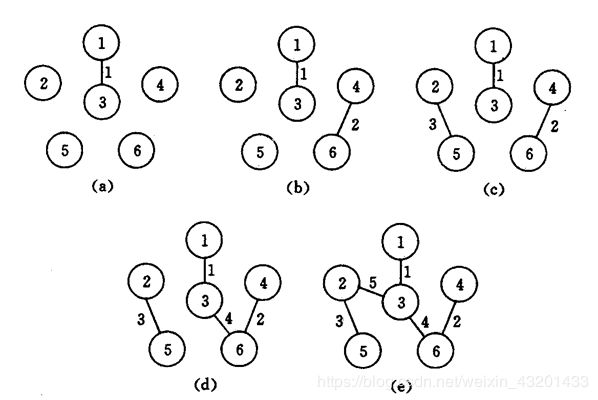
①Prime Algorithm(按顶点)
算法介绍
这种算法特别适用于边数相对较多,即比较接近于完全图的图。
此算法是按逐个将顶点连通的步骤进行的,它只需采用一个顶点集合。这个集合开始时是空集,以后将已连通的顶点陆续加入到集合中去,到全部顶点都加入到集合中了,就得到所需的生成树。
算法步骤
•设G=(V,E)是一个连通带权图,V={1,2,…,n}。
• 构造G的一棵最小生成树的Prim算法的过程是:
• 首先从图的任一顶点起进行,将它加入集合S中置,S={1},
• 然后作如下的贪婪选择,从与之相关联的边中选出权值c[i][j]最小的一条作为生成树的一条边,
• 此时满足条件i ∈ S,j ∈ V-S,并将该j加入集合中,表示连两个顶点已被所选出的边连通了。
•以后每次从一个端点在集合S中而另一个端点在集合S外的各条边中选取权值最小的一条作为生成树的一条边,并把其在集合外的那个顶点加入到集合S中。
• 如此进行下去,直到全部顶点都加入到集合中S。
• 在这个过程中选取到的所有边恰好构成G的一棵最小生成树。
• 由于Prim算法中每次选取的边两端总是一个已连通顶点和一个未连通顶点,故这个边选取后一定能将该未连通点连通而又保证不会形成回路。
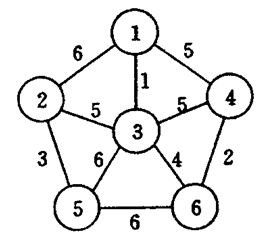
例题1
例题2
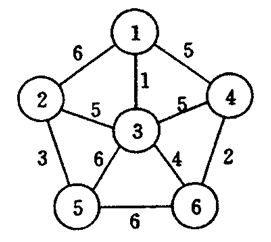
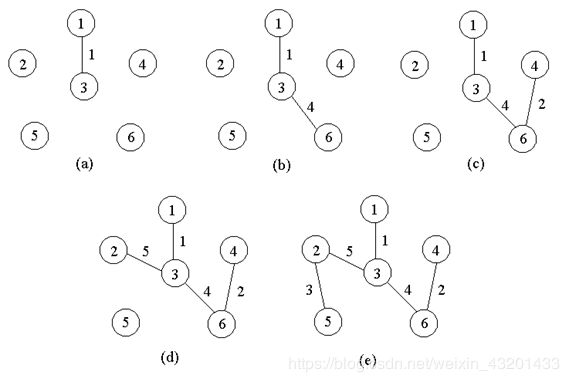
②Kruskal Algorithm(按边)
算法步骤
•设G=(V,E)是一个连通带权图,V={1,2,…,n}。
•将图中的边按其权值由小到大排序, 然后作如下的贪婪选择,由小到大顺序选取各条边,若选某边后不形成回路,则将其保留作为树的一条边;若选某边后形成回路,则将其舍弃,以后也不再考虑。
• 如此依次进行,到选够(n-1)条边即得到最小生成树。
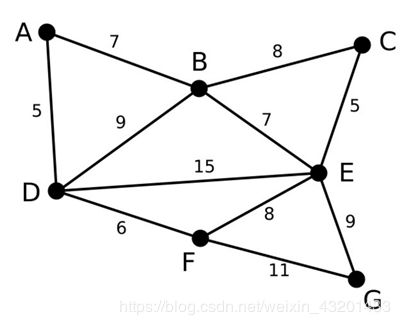
例题
6.完美字符串(就是统计出现次数最多的字符)
问题描述
约翰认为字符串的完美度等于它里面所有字母的完美度之和。每个字母的完美度可以由你来分配,不同字母的完美度不同,分别对应一个1-26之间的整数。
约翰不在乎字母大小写。(也就是说字母F和f)的完美度相同。给定一个字符串,输出它的最大可能的完美度。例如:dad,你可以将26分配给d,25分配给a,这样整个字符串完美度为77。
输入 输入一个字符串S(S的长度 <= 10000),S中没有除字母外的其他字符。
输出 由你将1-26分配给不同的字母,使得字符串S的完美度最大,输出这个完美度。
输入示例 dad 输出示例 77
问题分析
#include
using namespace std;
char s[10000+10];
int mp[100];
int b[100];
int main()
{
cin>>s;
int p=0;
int l=strlen(s);
memset(mp,0,sizeof(mp));
memset(b,0,sizeof(b));
for(int i=0;i='a'&&s[i]<='z') p=s[i]-'a';//0~25
if(s[i]>='A'&&s[i]<='Z') p=s[i]-'A';//0~25
mp[p]++;//每个字母出现的次数
}
int sum=0,k=26;
sort(mp,mp+26);
for(int i=25;i>=0;i--)
{
if(mp[i]==0) continue;
sum+=k*mp[i];
k--;
}
cout< 7.一个我取不出名的问题,叫‘删数问题’8
问题描述
键盘输入一个高精度的正整数N,去掉其中任意S个数字后剩下的数字按原左右次序将组成一个新的正整数。编程对给定的N和S,寻找一种方案使得剩下的数字组成的新数最小。
8.多机调度问题
①一台机器n个零件
某车间只有一台高精度的磨床,常常出现很多零件同时要求这台磨床加工的情况,现有六个零件同时要求加工,这六个零件加工所需时间如右表所示。应该按照什么样的加工顺序来加工这六个零件,才能使得这六个零件在车间里停留的平均时间为最少?
用Pi表示安排在第i位加工的零件所需的时间,用Tj表示安排在第j位加工的零件在车间里总的停留时间,则这六个零件的停留时间为:
T1 + T2 + T3 + T4 + T5 + T6
= P1 + ( P1 + P2 ) + (P1 + P2 + P3 ) + (P1 + P2 + P3 + P4 ) +
(P1 + P2 + P3 + P4 + P5) + (P1 + P2 + P3 + P4 + P5 + P6 )
= 6 P1 + 5 P2 + 4P3 + 3P4 + 2P5 + P6
由上式可知,把加工时间最短的放在P1的位置即首先安排加工即可(略过8,飞~)
②2台机器n个零件
目的:使得完成全部工作的总时间最短。
某车间需要用一台车床和一台铣床加工A、B、C、D四个零件。每个零件都需要先用车床加工,再用铣床加工。车床与铣床加工每个零件所需的工时(包括加工前的准备时间以及加工后的处理时间)如表。
| 工时(小时) |
A |
B |
C |
D |
| 车床 |
8 |
6 |
2 |
4 |
| 铣床 |
3 |
1 |
3 |
12 |
那么上面这个题的顺序安排就应该是CDAB 用时为22
再来一个例题:
| 工时(小时) |
A |
B |
C |
D |
| 车床 |
8 |
4 |
6 |
6 |
| 铣床 |
6 |
10 |
2 |
5 |
由上面的内容可知,最短时间的顺序应该是BDAC/BADC 它们两种策略计算时间都是27
9.数列极差问题
问题描述
在黑板上写了N个正整数作成的一个数列,进行如下操作:每一次擦去其中的两个数a和b,然后在数列中加入一个数a×b+1,如此下去直至黑板上剩下一个数,在所有按这种操作方式最后得到的数中,最大的记作max,最小的记作min,则该数列的极差定义为M=max-min。
和上一个例题一样,我们通过实例来认识题目中描述的计算过程。对三个具体的数据3,5,7讨论,可能有以下三种结果:
(3*5+1)*7+1=113
(3*7+1)*5+1=111
(5*7+1)*3+1=109
!!!由此可见,先运算小数据得到的是最大值,先运算大数据得到的是最小值。
下面再以三个数为例证明此题用贪心算法求解的合理性,不妨假设:a
(a*b+1)*c+1=a*a*a+(2k1+k2)a*a+(k1(k1+k2)+1)*a+k1+k2+1
(a*c+1)*b+1=a*a*a+(2k1+k2)a*a+(k1(k1+k2)+1)*a+k1+1
(b*c+1)*a+1=a*a*a+(2k1+k2)a*a+(k1(k1+k2)+1)*a+1
显然此问题适合用贪心算法,不过在求最大值时,要先选择较小的数操作。反过来求最小值时,要先选择较大的数操作。这是一道两次运用贪心算法解决的问题。
问题分析
这个问题就是循环找出最大两个数和最小两个数进行计算。
算法复杂度的话,就是比较和查找,比较的复杂度是O(n),空间复杂度是O(2n)因为要用两个数组保存分别保存最大和最小的数。
#include
using namespace std;
//定义两个数组用于求最大和最小值得时候使用
int s[50001];
int j[50001];
int cmp(int a,int b){
return a>b;
}
int main(){
int n;
while(cin>>n&&n){
for(int i=0;i>s[i];
j[i]=s[i];
}
//先升序排列
sort(s,s+n);
for(int i=1;i 10.分马问题
问题描述
老人弥留之际,将家中11匹马分给3个儿子,老大1/2,老二1/4,老三1/6。二分之一是5匹半马,总不能把马杀了吧,正在无奈之际,邻居把自己家的马牵来,老大二分之一,牵走了6匹;老二四分之一,牵走了3匹;老三六分之一,牵走了2匹。一共11匹,分完后,邻居把自己的马牵了回去。即11/12=1/2+1/4+1/6。这种分子是1的分数,叫作埃及分数,因为古代埃及人在进行分数运算时,只使用分子是1的分数。
设计一个算法, 把一个真分数表示为埃及分数之和的形式。如:7/8=1/2+1/3+1/24
问题分析
基本思想是, 逐步选择分数所包含的最大埃及分数,这些埃及分数之和就是问题的一个解。
如:7/8>1/2,
7/8-1/2>1/3,
7/8-1/2-1/3=1/24。
算法过程如下:
1)找最小的n,使分数f>1/n;
2)输出1/n;
3)计算f=f-1/n;
4)若此时的f是埃及分数,输出f,算法结束,否则返回(1)
----------------------------然而....高级程序语言不支持分数运算,所以上面这些都可以略过了----------------------------------------
实际的算法步骤其实是这样的:
记真分数F=A/B;对B/A进行整除运算,商为D, 余数为K(0<K<A),它们之间的关系及导出关系如下:
B=A*D+K,B/A=D+K/A<D+1,A/B>1/(D+1),记C=D+1。
这样我们就找到了分数F所包含的“最大的”埃及分数就是1/C。进一步计算:
A/B-1/C=(A*C-B)/B*C
也就是说继续要解决的是有关分子为A=A*C-B,分母为B=B*C的问题。
--------------------------------------------------------------------------------------------------------------------
由以上数学模型,真正的算法过程如下:
1)设某个真分数的分子为A(≠1),分母为B;
2)把B除以A的商的整数部分加1后的值作为埃及分数的一个分母C;
3)输出1/C;
4)将A乘C减去B作为新的A;
5)将B乘C作为新的B;
6)如果A大于1且能整除B,则最后一个分母为B/A;
7)如果A=1,则最后一个分母为B;否则转步骤(2).
下面用具体的实例来对算法进行模拟
例:7/8=1/2+1/3+1/24的解题步骤:
同样用变量A表示分子,变量B表示分母;
C=8/7+1=2 //说明7/8>1/2,
打印1/2
A=7*2-8=6,B=B*C=16
//在计算7/8-1/2=(7*2-8)/(7*2)=6/16=A/B
C=16/6+1=3 //说明16/6>1/3,
打印1/3
A=6*3-16=2,B=B*C=16*3=48
//在计算6/16-1/3=(6*3-16)/(16*3)=2/48=A/B
A>1但B/A为整数24,打印1/24 结束.
其实程序都不是很重要了,因为算法每一步弄懂就可以了,程序只是一种模拟。
#include
using namespace std;
int main( )
{
int a,b,c;
scanf("%d%d",&a,&b);
if(a>b)
printf("input error\n");
else if (a==1 || b % a==0)
printf("%d/%d=1/%d\n",a,b,b/a);
else
{ while(a!=1)
{
c = b / a + 1;
a = a * c - b;
b = b * c;
printf( "1/%d",c);
if( a > 1)
printf(" + ");
if (b % a==0 || a==1 )
{
printf ("1/%d",b / a);
a=1;
}
}
}
return 0;
} 11.取数游戏
问题描述
有2个人轮流取2n个数中的n个数,取数之和大者为胜,取数者只能看到2n个数中两边的数。请编写算法,让先取数者胜,模拟取数过程。
若一组数据为:6,16,27,6,12,9,2,11,6,5。用贪心算法每次两人都取两边的数中较大的一个数,先取者胜。
以A先取为例, 取数结果为:
A 6,27,12,5,11=61 胜
B 16,6,9,6,2=39
但若选另一组数据:16,27,7,12,9,2,11,6。仍都用贪心算法,先取者A败。取数结果为:
A 16,7,9,11=43
B 27,12,6,2=47 胜
其实,若我们只能看到两边的数据,则此题无论先取还是后取都无必胜的策略。
但若取数者能看到全部2n个数,则此问题可有一些简单的方法,有的虽不能保证所取数的和是最大,但确是一个先取者必胜的策略。
问题分析
①数学模型
N个数排成一行,从左到右编号,依次为1,2,…,N,我们先取数,计算机后取数,所以一开始我们既可以取到一个奇编号的数(最左边编号为1的数)又可以取到一个偶编号的数(最右边编号为N的数)。
如果我们第一次取奇编号(编号为1)的数,则接着计算机只能取到偶编号(编号为2或N)的数;
如果我们第一次取偶编号(编号为N)的数,则接着计算机只能取到奇编号(编号为1或N-1)的数;
即无论我们第一次是取奇编号的数还是取偶编号的数,接着计算机只能取到另一种编号(偶编号或奇编号)的数。
这是对第一个回合的分析,显然对以后整个取数过程都适用。也就是说,我们能够控制让计算机自始自终只取一种编号的数。这样,我们只要比较奇编号数之和与偶编号数之和谁大,以决定最开始我们是取奇编号数还是偶编号数即可。如果奇编号数之和与偶编号数之和同样大,我们第一次可以任意取数,因为当两者所取数和相同时,先取者为胜。
②问题解决
有了以上建立的高效数学模型,算法就很简单了,算法只需要分别计算一组数的奇数位和偶数位的数据之和,然后就先了取数者就可以确定必胜的取数方式了。
以下面一排数为例:
1 2 3 10 5 6 7 8 9 4
奇编号数之和为25(=1+3+5+7+9),小于偶编号数之和为30(=2+10+6+8+4)。我们第一次取4,以后,计算机取哪边的数我们就取哪边的数(如果计算机取1,我们就取2;如果计算机取9,我们就取8)。这样可以保证我们自始自终取到偶编号的数,而计算机自始自终取到奇编号的数。
12.整数分解然后计算最大乘积(这个怕不是作业)
问题描述
设n是一个正整数,现在要求将n分解为若干不相同的自然数的和,且使这些自然数的乘积最大。
输入:10
输出:30
问题分析
#include
using namespace std;
int main()
{
int n;
cin >> n;
int k = 2;
int a[100] = {0};
int i = 0;
while(n >= k) //分解:从2开始减直到0
{
a[i++] = k;
n -= k;
k++;
}
if(n) //如果差是0,则乘起来就可以得到结果,否则将差从后往前顺序分配
{
if(n == a[i - 1])
{
a[i - 1]++;
n --;
}
for(int j = 0;j < n;j++) //从后往前均匀分配
a[i - 1 - j]++;
}
int res = 1;
for(int j = 0;j <=i - 1;j++)
res *= a[j];
cout< 13.顾客等待问题(这个怕不也是作业)
问题描述
设有n个顾客同时等待一项服务。顾客i需要的服务时间为ti,1≤i≤n。共有s处可以提供此项服务。应如何安排n个顾客的服务次序才能使平均等待时间达到最小?平均等待时间是n个顾客等待服务时间的总和除以n 。
输入:第一行有2个正整数n和s,表示有n个顾客且有s处可以提供服务,接下一行表示n个顾客需要的服务时间。
输出:最小平均等待时间。
输入样例:
10 2
56 12 1 99 1000 234 33 55 99 812
输出样例:
336
#include
#include
int cmp(const void *a, const void *b)
{
return (*(int *)a - *(int *)b);
}
int main()
{
int i = 0, j = 0; //控制程序流程
int n, s; //n:顾客数目; s:服务处数目
double t = 0; //统计最终的平均等待时间
int a[100]; //记录各个顾客的服务时间
int st[100] = {0}; //S个服务处服务时间记录
printf("请输入顾客(n)和服务处数目(s):");
scanf("%d%d", &n, &s); //输入顾客数目和服务处数目
printf("\n请输入各个顾客的服务时间a:\n");
for(i = 0; i < n; i++) //依次输入各个顾客服务时间
scanf("%d", &a[i]);
qsort(a,n,sizeof(a[0]),cmp); //排序函数--快排思想
//sort(a,a+n);
i=0;
while(i < n)
{
st[j] +=a [i];
t += st[j];
i++;
j++;
if(j == s)
j = 0;
}
printf("\n平均等待时间:");
printf("%.f\n",t/n);
//flushall();
printf("按任意键继续...");
getchar();
return 0;
}