深蓝学院《从零开始手写VIO》作业二

深蓝学院《从零开始手写VIO》作业二

1. 设置IMU仿真中的不同的参数，生成allen方差标定曲线

allen方差工具：
https://github.com/gaowenliang/imu_utils

在这题中我一共进行了三次实验，三次实验中加速度计以及陀螺仪的高斯白噪声和Bias随机游走噪声的大小是成等比例（比例为10）进行放大和缩小，下面先摆出实验结果然后分析实验数据

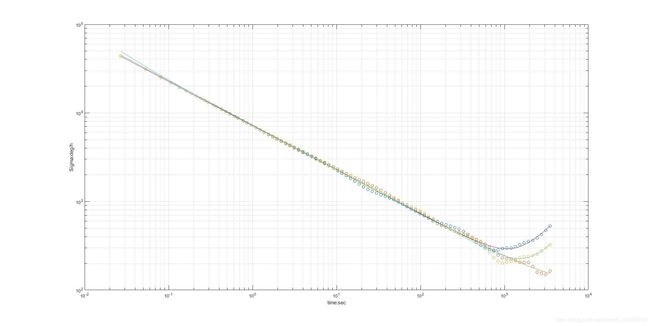
（1）噪声较小的情况

a. 参数设置
此参数设置在vio_data_simulation-ros_version/src/param.h中，分别是加速度计以及陀螺仪的高斯白噪声和Bias随机游走噪声的大小

    double gyro_bias_sigma = 0.000005;
    double acc_bias_sigma = 0.00005;

    double gyro_noise_sigma = 0.0015;    
    double acc_noise_sigma = 0.0019;      

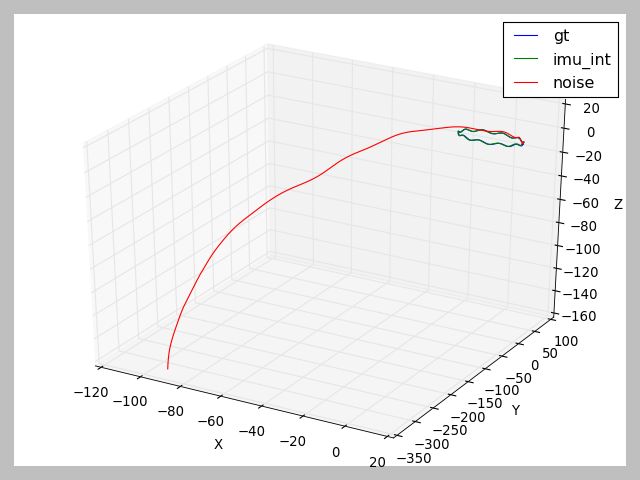
b. 仿真结果
以下是由vio_data_simulation-master/main/gener_alldata.cpp生成数据，由vio_data_simulation-master/python-tool/draw_trajcory.py生成

c. 利用仿真工具画allen曲线并获得噪声估计结果
allen曲线为（这里是在静止的情况下测量的，另外抱歉这里有点看不清，纵坐标从上到下分别是$10^4,10^3.10^2,10^1$）：

噪声估计结果为：

Gyr:
   unit: " rad/s"
   avg-axis:
      gyr_n: 2.1016644346403605e-02
      gyr_w: 1.3328766989568059e-04
Acc:
   unit: " m/s^2"
   avg-axis:
      acc_n: 2.6763958793439523e-02
      acc_w: 4.6470131356570474e-04

（2）噪声中等的情况

a. 参数设置
此参数设置在vio_data_simulation-ros_version/src/param.h中，分别是加速度计以及陀螺仪的高斯白噪声和Bias随机游走噪声的大小

    double gyro_bias_sigma = 0.00005;
    double acc_bias_sigma = 0.0005;

    double gyro_noise_sigma = 0.015;   
    double acc_noise_sigma = 0.019;  

b. 仿真结果
以下是由vio_data_simulation-master/main/gener_alldata.cpp生成数据，由vio_data_simulation-master/python-tool/draw_trajcory.py生成

c. 利用仿真工具画allen曲线并获得噪声估计结果
allen曲线为（这里是在静止的情况下测量的，另外抱歉这里有点看不清，纵坐标从上到下分别是$10^5,10^4,10^3.10^2$）：

噪声估计结果为：

Gyr:
   unit: " rad/s"
   avg-axis:
      gyr_n: 2.1426963216977588e-01
      gyr_w: 1.0886455204925014e-03
Acc:
   unit: " m/s^2"
   avg-axis:
      acc_n: 2.6881801136204303e-01
      acc_w: 4.9716963622466080e-03

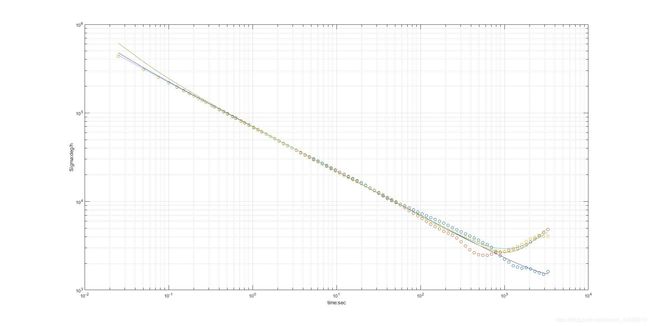
（3）噪声较大的情况

a. 参数设置
此参数设置在vio_data_simulation-ros_version/src/param.h中，分别是加速度计以及陀螺仪的高斯白噪声和Bias随机游走噪声的大小

    double gyro_bias_sigma = 0.0005;
    double acc_bias_sigma = 0.005;

    double gyro_noise_sigma = 0.15;    
    double acc_noise_sigma = 0.19;      

b. 仿真结果
以下是由vio_data_simulation-master/main/gener_alldata.cpp生成数据，由vio_data_simulation-master/python-tool/draw_trajcory.py生成

c. 利用仿真工具画allen曲线并获得噪声估计结果
allen曲线为（这里是在静止的情况下测量的，另外抱歉这里有点看不清，纵坐标从上到下分别是$10^6,10^5,10^4,10^3$）：

噪声估计结果为：

Gyr:
   unit: " rad/s"
   avg-axis:
      gyr_n: 2.1370768874875155e+00
      gyr_w: 4.8477797168896648e-03
Acc:
   unit: " m/s^2"
   avg-axis:
      acc_n: 2.6832843026523694e+00
      acc_w: 4.9509703964721895e-02

（4） 实验结果分析

我上述实际噪声大小和标定结果汇总到下面表格中进行对比分析：
加速度计：

加速度计Bias随机游走大小	实际大小	标定结果	标定结果离散化后结果
小噪声	0.0019	2.6763958793439523e-02	0.00188769
中噪声	0.019	2.6881801136204303e-01	0.0189476
大噪声	0.19	2.6832843026523694e+00	0.189476

加速度计高斯白噪声大小	实际大小	标定结果	标定结果离散化后结果
小噪声	0.00005	4.6470131356570474e-04	0.0065728
中噪声	0.0005	4.9716963622466080e-03	0.0703209
大噪声	0.005	4.9509703964721895e-02	0.700268

陀螺仪：

陀螺仪Bias随机游走大小	实际大小	标定结果	标定结果离散化后结果
小噪声	0.0015	2.1016644346403605e-02	0.001485407
中噪声	0.019	2.1426963216977588e-01	0.01514394
大噪声	0.19	2.1370768874875155e+00	0.1510859

陀螺仪高斯白噪声大小	实际大小	标定结果	标定结果离散化后结果
小噪声	0.000005	1.3328766989568059e-04	0.001885148
中噪声	0.00005	1.0886455204925014e-03	0.01539801
大噪声	0.0005	4.8477797168896648e-03	0.06856817

这里对标定结果离散采用的公式是
高斯白噪声：$${\sigma }_d=\sigma \frac{1}{\sqrt{\Delta t}}$$Bias随机游走大小：$${\sigma }_{bd}={\sigma }_b\sqrt{\Delta t}$$通过上面的对比可以发现，加速度计和陀螺仪的Bias随机游走大小allen方差的估计是较为准确的，但是高斯白噪声的估计却差了几个数量级，在陀螺仪大噪声的情况下还出现了一次数据较大的偏差，课程视频上贺博也解释了这种情况是正常的（大噪声情况下的数据偏差应该是不正常的），在实际的IMU使用中是对估计出来的白噪声进行等比例系数处理的。

2. 将IMU仿真代码中的欧拉积分替换成中值积分

（1）通过t-1和t时刻的值来计算中值

代码如下：

MotionData next_imupose = imudata[i+1];
//delta_q = [1 , 1/2 * thetax , 1/2 * theta_y, 1/2 * theta_z]
Eigen::Quaterniond dq;
Eigen::Vector3d dtheta_half =  (imupose.imu_gyro + last_imupose.imu_gyro) * dt / 4.0;
dq.w() = 1;
dq.x() = dtheta_half.x();
dq.y() = dtheta_half.y();
dq.z() = dtheta_half.z();
/// 中值积分
Qwb = last_Qwb * dq;
Eigen::Vector3d acc_w = 0.5*(last_Qwb*(last_imupose.imu_acc)+Qwb*(imupose.imu_acc)+2*gw);
Vw = Vw + acc_w * dt;
Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;
last_Qwb = Qwb;

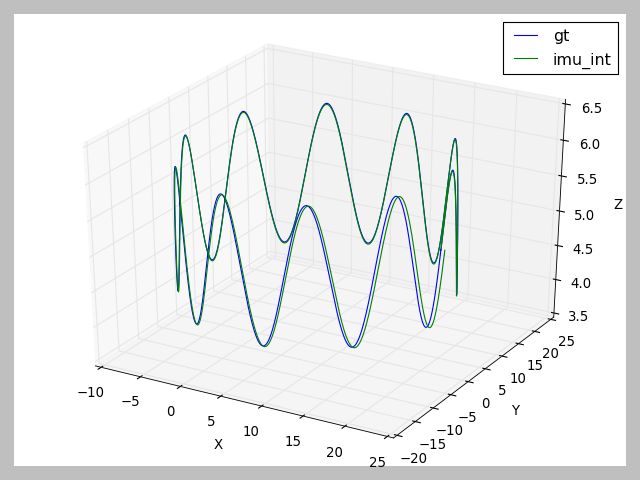
结果如下：

（2）通过t+1和t时刻的值来计算中值

代码如下：

MotionData last_imupose = imudata[i-1];
//delta_q = [1 , 1/2 * thetax , 1/2 * theta_y, 1/2 * theta_z]
Eigen::Quaterniond dq;
Eigen::Vector3d dtheta_half =  (imupose.imu_gyro + next_imupose.imu_gyro) * dt / 4.0;
dq.w() = 1;
dq.x() = dtheta_half.x();
dq.y() = dtheta_half.y();
dq.z() = dtheta_half.z();
/// 中值积分
Eigen::Vector3d acc_w = 0.5*(Qwb*(imupose.imu_acc)+Qwb*dq*(imupose.imu_acc)+2*gw);
Qwb = Qwb * dq;
Vw = Vw + acc_w * dt;
Pwb = Pwb + Vw * dt + 0.5 * dt * dt * acc_w;

结果如下：

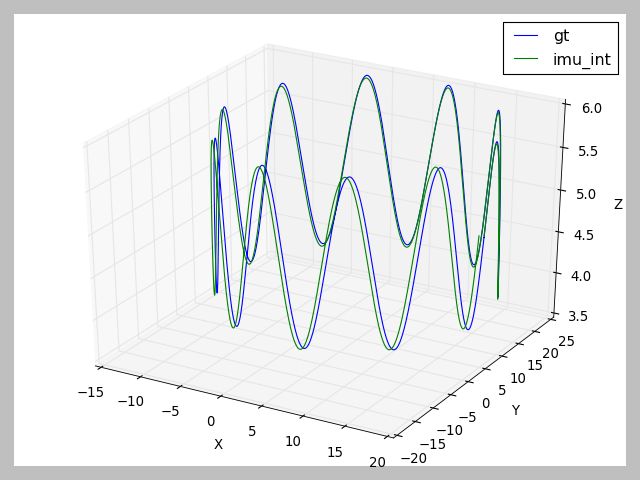
（3）实验结果分析

这里我们通过对比欧拉积分的结果：

可以看出来，正确的中值积分（第一种）的结果是要优于欧拉积分的，而上面第二种积分结果明显是公式搞错了…

3. 论文阅读

阅读论文《Spline Fusion: A continuous-time representation for visual-inertial fusion with application to rolling shutter cameras》总结推导过程如下：
$k-1$阶的B次样条曲线如下：$$\mathbf{p}(t)=\sum _{i=0}^n{\mathbf{p}}_i{B}_{i,k}(t)$$其中，${\mathbf{p}}_i\in {\mathbb{R}}^N$是$t_i,i\in [0,\dots ,n]$时刻的控制点，$B_{i,k}(t)$是基函数，如下$$B_{i,0}(x):=\{\begin{array}{ll}1& \text{ if }{t}_i\le x<t_{i+1}\\ 0& \text{ otherwise }\end{array}$$$$B_{i,p}(x):=\frac{x-t_i}{t_{i+p}-t_i}{B}_{i,p-1}(x)+\frac{t_{i+p+1}-x}{t_{i+p+1}-t_{i+1}}{B}_{i+1,p-1}(x)$$上式可以累计形式如下：$$\mathbf{p}(t)={\mathbf{p}}_0{\tilde{B}}_{0,k}(t)+\sum _{i=1}^n\left({\mathbf{p}}_i-{\mathbf{p}}_{i-1}\right){\tilde{B}}_{i,k}(t)$$其中${\tilde{B}}_{i,k}(t)={\sum }_{j=i}^n{B}_{j,k}(t)$累计基函数，然后通过用控制点之间的对数变换${\Omega }_i=\log \left({\mathbf{T}}_{w,i-1}^{-1}{\mathbf{T}}_{w,i}\right)$操作代替控制点之差来描述SE3中的轨迹，上式可以进一步变换成：$${\mathbf{T}}_{w,s}(t)=\exp \left({\tilde{B}}_{0,k}(t)\log \left({\mathbf{T}}_{w,0}\right)\right)\prod _{i=1}^n\exp \left({\tilde{B}}_{i,k}(t){\Omega }_i\right)$$其中${\mathbf{T}}_{w,s}(t)\in \mathbb{S}\mathbb{E}3$是样条曲线上t时刻的位姿，而${\mathbf{T}}_{w,i}\in \mathbb{S}\mathbb{E}3$就是世界坐标系下控制点位姿。
再本文中，主要研究的是四次累计B样条曲线，也就四说对于$t\in \left[t_i,t_{i+1}\right)$这段时间中一共有$\left[t_{i-1},t_i,t_{i+1},t_{i+2}\right]$四个控制点来确定时刻$t$的样条曲线上的值，我们使用$s(t)=\left(t-t_0\right)/\Delta t$来表示平均时间的函数，那么控制点的时刻$t_i$就可以由平均时间函数$s_i\in [0,1,\dots ,n]$来表示，对于时间$s_i\le s(t)<s_{i+1}$，我们就可以定义这样一个$u(t)=s(t)-s_i$这样一个函数来表示，上面其实就是说我们定义一个累加式的时间函数来表示控制点之间的时刻的位置。有了上面的基础文中说我们就可以重写矩阵形式的B样条曲线以及它的一阶二阶微分函数如下：$$\tilde{\mathbf{B}}(u)=\mathbf{C}\left[\begin{array}{c}1\\ u\\ u^2\\ u^3\end{array}\right],\dot{\mathbf{B}}(u)=\frac{1}{\Delta t}\mathbf{C}\left[\begin{array}{c}0\\ 1\\ 2u\\ 3u^2\end{array}\right],\ddot{\mathbf{B}}(u)=\frac{1}{\Delta t^2}\mathbf{C}\left[\begin{array}{c}0\\ 0\\ 2\\ 6u\end{array}\right],\mathbf{C}=\frac{1}{6}\left[\begin{array}{cccc}6& 0& 0& 0\\ 5& 3& -3& 1\\ 1& 3& 3& -2\\ 0& 0& 0& 1\end{array}\right]$$然后轨迹上的位姿可以定义为$${\mathbf{T}}_{w,s}(u)={\mathbf{T}}_{w,i-1}\prod _{j=1}^3\exp \left(\tilde{\mathbf{B}}(u{)}_j{\Omega }_{i+j}\right)$$其中$i$下标表示时间$t$所在的时间间隔区间，简单地理解上面的公式推导过程就是我如果要求时刻$t\in \left[t_i,t_{i+1}\right)$的四次B样条曲线上的位姿，我需要根据$i-1$时刻的位姿${\mathbf{T}}_{w,i-1}$，利用上面的公式直接求出来，又因为这个公式是一个连续公式，因此可以求它的一阶导数和二阶导数，也就是对应的速度和加速度，如下：$${\mathbf{T}}_{w,s}(u)={\mathbf{T}}_{w,i-1}\left({\dot{\mathbf{A}}}_0{\mathbf{A}}_1{\mathbf{A}}_2+{\mathbf{A}}_0{\dot{\mathbf{A}}}_1{\mathbf{A}}_2+{\mathbf{A}}_0{\mathbf{A}}_1{\dot{\mathbf{A}}}_2\right)$$$${\ddot{\mathbf{T}}}_{w,s}(u)={\mathbf{T}}_{w,i-1}\left(\begin{array}{c}{\ddot{\mathbf{A}}}_0{\mathbf{A}}_1{\mathbf{A}}_2+{\mathbf{A}}_0{\ddot{\mathbf{A}}}_1{\mathbf{A}}_2+{\mathbf{A}}_0{\mathbf{A}}_1{\ddot{\mathbf{A}}}_2+\\ 2\left({\dot{\mathbf{A}}}_0{\mathbf{A}}_1{\mathbf{A}}_2+{\dot{\mathbf{A}}}_0{\mathbf{A}}_1{\mathbf{A}}_2+{\mathbf{A}}_0{\mathbf{A}}_1{\dot{\mathbf{A}}}_2\right)\end{array}\right)$$$$\begin{array}{rl}{\mathbf{A}}_j& =\exp \left({\Omega }_{i+j}\tilde{\mathbf{B}}(u{)}_j\right),{\dot{\mathbf{A}}}_j={\mathbf{A}}_j{\Omega }_{i+j}\dot{\mathbf{B}}(u{)}_j\\ {\ddot{\mathbf{A}}}_j& ={\mathbf{A}}_j{\Omega }_{i+j}\hat{\mathbf{B}}(u{)}_j+{\mathbf{A}}_j{\Omega }_{i+j}\tilde{\mathbf{B}}(u{)}_j\end{array}$$

接下来就是将推导出来样条曲线应用到实际的惯性视觉数据上来

首先我们可以将一个空间点在两帧$a,b$上的图像坐标表示为：$${\mathbf{p}}_b=\mathcal{W}\left({\mathbf{p}}_a;{\mathbf{T}}_{b,a},\rho \right)=\pi \left(\left[{\mathbf{K}}_b|0\right]{\mathbf{T}}_{b,a}\left[{\mathbf{K}}_a^{-1}\left[\begin{array}{c}{\mathbf{p}}_a\\ 1\end{array}\right];\mathbf{\rho }\right]\right)$$其中$\pi (\mathbf{P})=\frac{1}{{\mathbf{P}}_2}{\left[{\mathbf{P}}_0,{\mathbf{P}}_1\right]}^{\top }$为归一化平面上坐标的投影方程，${\mathbf{K}}_a,{\mathbf{K}}_b\in {\mathbb{R}}^{3\times 3}$分别是两帧图像的内参，然后利用上面推导出来B样条曲线的公式，我们可以生成加速度计和陀螺仪的测量模型：$$\begin{array}{rl}\mathrm{Gyro}(u)& ={\mathbf{R}}_{w,s}^{\top }(u)\cdot {\dot{\mathbf{R}}}_{w,s}(u)+\text{ bias }\\ \mathrm{Accel}(u)& ={\mathbf{R}}_{w,s}^{\top }(u)\cdot \left({\mathbf{s}}_w(u)+g_w\right)+\text{ bias }\end{array}$$其中角速度${\dot{\mathbf{R}}}_{w,s}$和加速度${\dot{\mathbf{S}}}_{\mathbf{W}}$分别是矩阵${\mathbf{T}}_{w,s}$和${\ddot{\mathbf{T}}}_{w,s}$的子矩阵，然后我们通过最小化下面这个由预测模型和实际观测构成的代价函数来求得曲线的参数$$\begin{array}{rl}E(\theta )=& \sum _{{\hat{\mathbf{p}}}_m}{\left({\hat{\mathbf{p}}}_m-\mathcal{W}\left({\mathbf{p}}_r;{\mathbf{T}}_{c,s}{\left(u_m\right)}^{-1}{\mathbf{T}}_{w,s}\left(u_r\right){\mathbf{T}}_{s,c},\rho \right)\right)}_{{\Sigma }_p}^2+\\ & \sum _{{\hat{\omega }}_m}{\left({\hat{\omega }}_m-\mathrm{Gyro}\left(u_m\right)\right)}_{{\Sigma }_{\omega }}^2+\sum _{{\hat{\mathbf{a}}}_m}{\left({\hat{\mathbf{a}}}_m-\mathrm{Accel}\left(u_m\right)\right)}_{{\Sigma }_{\mathbf{a}}}^2\end{array}$$其中${\hat{\mathbf{p}}}_m,{\hat{\omega }}_m$,${\hat{\mathbf{a}}}_m$就是测量值

总而言之，本文的大概思路是通过用四次B样条曲线来拟合相机的轨迹，而不是通过我们一般的思路建立运动学公式然后通过观测来对运动学公式进行修正这样的思路，文中提到这样做的一个优势是能很好地利用最小二乘法标定不同步时间的内外参矩阵，我想大概能了解其中的含义。

4. 附录

做作业中遇到的问题：

这次遇到的问题主要是在运行allen方差工具的时候环境配置的问题，我开始是尝试安装最新版本的ceres和Eigen，但是发现编译的时候会遇到ceres中Eigen的编译错误，纠结了很久，后来怀疑是不是最新版本的ceres和Eigen版本不匹配，因为就尝试卸载最新版的Eigen重新装了Eigen3.2，然后就好使了，中间耽误了不少时间，环境搞死人…