Tensorflow实战（一）

tensorflow常用方法

#创建变量
w = tf.Variable([[0.5,1.0]])
x = tf.Variable([[2.0],[1.0]])

#乘法  加法
y = tf.matmul(w,x)
y = tf.add(y,b)
#打印结果
print(y.eval())

#创建常量
tensor = tf.zeros([3,4],int32)#常用于b的初始化
tensor = tf.ones([3,4],int32)
tensor = tf.constant([1,2,3,4,5,6])
tensor = tf.condtant(1,shape = [2,3])
#切片式常量
tensor = tf.linspace(10.0,12.0,3, name = "linspace") #10.0到12.0之间取三个数
tensor = tf.range(3，18，3)#3到18每3个数取一个值

#高斯分布
norm = tf.random_normal([2,3],mean = -1,stddev = 4)  #初始化W

#洗牌操作
shuff = tf.random_shuffle(x)

#赋值操作
update = tf.assign(state, value)

#初始化变量
init_op = tf.global_variables_initializer()

#按行取最大
tf.argmax(actv,1)
#按列取最大
tf.argmax(actv,0)

#判断两个张量是否相等，相等返回Ture,不等返回False
pred = tf.equal(tf.argmax(actv, 1), tf.argmax(y, 1))
#转换数据类型
accur = tf.cast(pred, "float")
#求平均
accr = tf.reduce_mean(accur)

#将numpy转换成tensor
import numpy as np
a = np.zeros((3,3))
ta = tf.convert_to_tensor(a)
with tf.Session() as sess:
     print(sess.run(ta))

arr = np.array([[31, 23,  4, 24, 27, 34],
                [18,  3, 25,  0,  6, 35],
                [28, 14, 33, 22, 20,  8],
                [13, 30, 21, 19,  7,  9],
                [16,  1, 26, 32,  2, 29],
                [17, 12,  5, 11, 10, 15]])
#打印数组维度
tf.rank(arr).eval()
#打印数组的形状
tf.shape(arr).eval()

#构建网络
#初始化参数
w_c1 = tf.Variable(w_alpha*tf.random_normal([3, 3, 1, 32]))  
b_c1 = tf.Variable(b_alpha*tf.random_normal([32]))  
#卷积层,"SAME"的意思时卷积之后尺寸不变
conv1 = tf.nn.relu(tf.nn.bias_add(tf.nn.conv2d(x, w_c1, strides=[1, 1, 1, 1], padding='SAME'), b_c1))  
#池化层
conv1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')  
conv1 = tf.nn.dropout(conv1, keep_prob)  
#全连接层
dense = tf.nn.relu(tf.add(tf.matmul(dense, w_d), b_d)) 

#在构建神经网络模型时占位
image = tf.placeholder('float', shape=shape)
output = net(image)
#得到结果需要feed_dict
features = output.eval(feed_dict={image: input_image_pre})

计算图

TensorFlow是一个通过计算图的形式来表述计算的编程系统；
基于TensorFlow这个编程系统中的每一个计算都是计算图上的一个节点，而节点与节点之间的连线则代表计算之间的依赖关系。

计算图工作的一个小栗子：

#一个值不断加一
#定义变量
state = tf.Variable(0)
new_value = tf.add(state, tf.constant(1))
update = tf.assign(state, new_value)

#构建图
with tf.Session() as sess:
    #初始化变量
    sess.run(tf.global_variables_initializer())
    #必须run一下才能打印出来
    print(sess.run(state))    
    for _ in range(3):
        sess.run(update)
        print(sess.run(state))

Tensorflow训练线性回归模型

1.生成样本

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

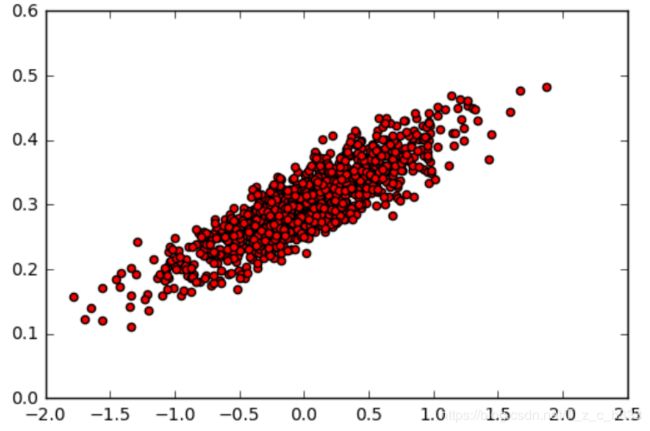
#随机生成1000个点，围绕在y=0.1x+0.3的直线周围
num_points = 1000
vectors_set = []
for i in range(num_points):
    x1 = np.random.normal(0.0, 0.55)
    y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03)
    vectors_set.append([x1, y1])

#生成一些样本
x_data = [v[0] for v in vectors_set]
y_data = [v[1] for v in vectors_set]

plt.scatter(x_data,y_data,c='r')
plt.show()

2.训练线性回归模型

#生成1维的W矩阵，取值是[-1,1]之间的随机数
with tf.name_scope('weight'):
    W = tf.Variable(tf.random_uniform([1], -1.0, 1.0), name='W')
#生成1维的b矩阵，初始值是0
with tf.name_scope('bias'):
    b = tf.Variable(tf.zeros([1]), name='b')
#经过计算得出预估值y
with tf.name_scope('y'):
    y = W * x_data + b

#以预估值y和实际值y_data之间的均方误差作为损失
with tf.name_scope('loss'):
    loss = tf.reduce_mean(tf.square(y - y_data), name='loss')
#采用梯度下降法来优化参数
optimizer = tf.train.GradientDescentOptimizer(0.5)
#训练的过程就是最小化这个误差值
train = optimizer.minimize(loss, name='train')

sess = tf.Session()

init = tf.global_variables_initializer()
sess.run(init)

#初始化的W和b是多少
print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss))
#执行20次训练
for step in range(20):
    sess.run(train)
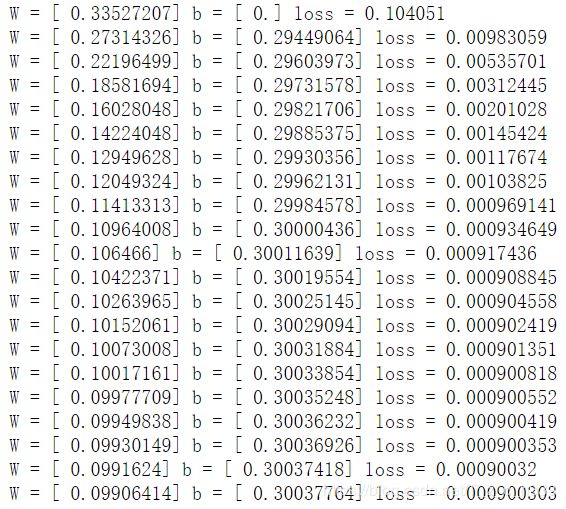
    # 输出训练好的W和b
    print ("W =", sess.run(W), "b =", sess.run(b), "loss =", sess.run(loss))
writer = tf.train.SummaryWriter("logs/", sess.graph)

3.得到模型

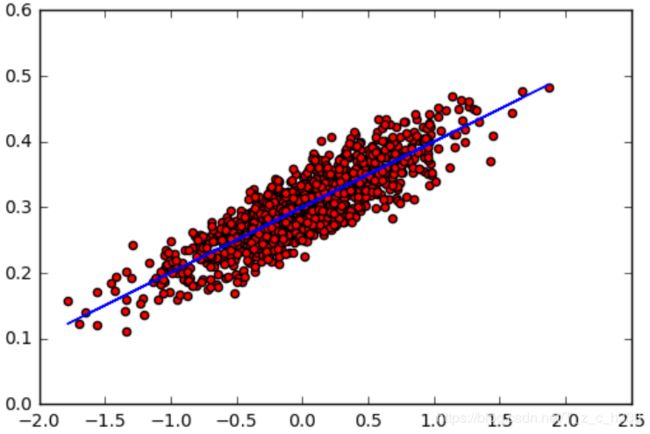
plt.scatter(x_data,y_data,c='r')
plt.plot(x_data,sess.run(W)*x_data+sess.run(b))
plt.show()