图&网络模型应用：最短路问题、 Dijkstra算法 、Floyd算法
图&网络系列博文：
【1】图与网络模型及方法：图与网络的基本概念
【2】图&网络模型应用—最短路径问题
【3】树：基本概念与最小生成树
【4】匹配问题： 匈牙利算法 、最优指派、相等子图
【5】Euler 图和 Hamilton 图
【6】计划评审方法和关键路线法【统筹方法】：广泛地用于系统分析和项 目管理
【7】最小费用流及其求法 ：
【8】最大流问题
【9】钢管订购和运输问题
目录
1 两个指定顶点之间的最短路径 Dijkstra算法
2 两个指定顶点之间最短路问题的数学表达式
例 2 最小价格管道铺设方案 例3 （无向图的最短路问题）
3 每对顶点之间的最短路径 Floyd算法
1 两个指定顶点之间的最短路径
问题如下：给出了一个连接若干个城镇的铁路网络，在这个网络的两个指定城镇间， 找一条最短铁路线。
Dijkstra算法
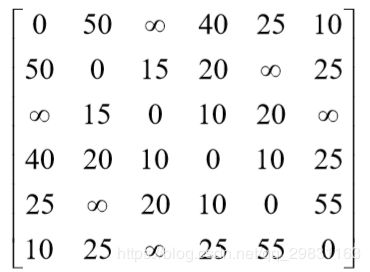
例1 某公司在六个城市
中有分公司，从 
到 
的直接航程票价记在如下矩阵的 
位置上。 （∞表示无直接航路），请帮助该公司设计一张城市 
到其它城市间的票价便宜的路线图。
解 用矩阵 
（n为顶点个数）存放各边权的邻接矩阵，行向量
分别用来存放P 标号信息、标号顶点顺序、标号顶点索引、短通路的值。其中分量
求第一个城市到其它城市的短路径的 Matlab 程序如下：
clc,clear
a=zeros(6);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a';
a(find(a==0))=inf;
pb(1:length(a))=0;pb(1)=1;index1=1;index2=ones(1,length(a));
d(1:length(a))=inf;d(1)=0;temp=1;
while sum(pb)2 两个指定顶点之间最短路问题的数学表达式
例 2 最小价格管道铺设方案
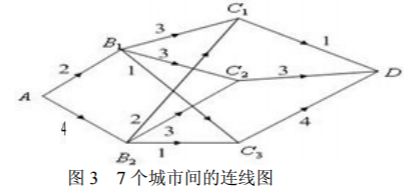
在图 3 中，用点表示城市，现有 A, B1, B2 ,C1,C2 ,C3 , D 共 7 个城市。点与 点之间的连线表示城市间有道路相连。连线旁的数字表示道路的长度。现计划从城市 A 到城市 D 铺设一条天然气管道，请设计出最小价格管道铺设方案。
编写 LINGO 程序如下：
model:
sets:
cities/A,B1,B2,C1,C2,C3,D/;
roads(cities,cities)/A B1,A B2,B1 C1,B1 C2,B1 C3,B2 C1,
B2 C2,B2 C3,C1 D,C2 D,C3 D/:w,x;
endsets
data:
w=2 4 3 3 1 2 3 1 1 3 4;
enddata
n=@size(cities); !城市的个数;
min=@sum(roads:w*x);
@for(cities(i)|i #ne#1 #and# i #ne#n:
@sum(roads(i,j):x(i,j))=@sum(roads(j,i):x(j,i)));
@sum(roads(i,j)|i #eq#1:x(i,j))=1;
@sum(roads(i,j)|j #eq#n:x(i,j))=1;
end 例3 （无向图的最短路问题）
求图 4 中 v1 到 v11的最短路。 分析 例 2 处理的问题属于有向图的最短路问题，本例是处理无向图的最短路问 题，在处理方式上与有向图的最短路问题有一些差别，这里选择赋权邻接矩阵的方法编 写 LINGO 程序。
编写 LINGO 程序如下：
model:
sets:
cities/1..11/;
roads(cities,cities):w,x;
endsets
data:
w=0;
enddata
calc:
w(1,2)=2;w(1,3)=8;w(1,4)=1;
w(2,3)=6;w(2,5)=1;
w(3,4)=7;w(3,5)=5;w(3,6)=1;w(3,7)=2;
w(4,7)=9;
w(5,6)=3;w(5,8)=2;w(5,9)=9;
w(6,7)=4;w(6,9)=6;
w(7,9)=3;w(7,10)=1;
w(8,9)=7;w(8,11)=9;
w(9,10)=1;w(9,11)=2;w(10,11)=4;
@for(roads(i,j):w(i,j)=w(i,j)+w(j,i));
@for(roads(i,j):w(i,j)=@if(w(i,j) #eq# 0, 1000,w(i,j)));
endcalc
n=@size(cities); !城市的个数;
min=@sum(roads:w*x);
@for(cities(i)|i #ne#1 #and# i #ne#
n:@sum(cities(j):x(i,j))=@sum(cities(j):x(j,i)));
@sum(cities(j):x(1,j))=1;
@sum(cities(j):x(j,1))=0; !不能回到顶点1;
@sum(cities(j):x(j,n))=1;
@for(roads:@bin(x));
end与有向图相比较，在程序中只增加了一个语句@sum(cities(j):x(j,1))=0，即 从顶点 1 离开后，再不能回到该顶点。
求得的最短路径为 1→2→5→6→3→7→10→9→11，最短路径长度为 13。
3 每对顶点之间的最短路径
计算赋权图中各对顶点之间最短路径，显然可以调用 Dijkstra 算法。具体方法是： 每次以不同的顶点作为起点，用 Dijkstra 算法求出从该起点到其余顶点的最短路径，反 复执行 n −1次这样的操作，就可得到从每一个顶点到其它顶点的最短路径。这种算法 的时间复杂度为 
。第二种解决这一问题的方法是由 Floyd R W 提出的算法，称 之为 Floyd 算法。
Floyd算法
例4 用Floyd算法求解例1。
矩阵path用来存放每对顶点之间最短路径上所经过的顶点的序号。Floyd算法的 Matlab程序如下：
clear;clc;
n=6; a=zeros(n);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a';
M=max(max(a))*n^2; %M为充分大的正实数
a=a+((a==0)-eye(n))*M;
path=zeros(n);
for k=1:n
for i=1:n
for j=1:n
if a(i,j)>a(i,k)+a(k,j)
a(i,j)=a(i,k)+a(k,j);
path(i,j)=k;
end
end
end
end
a, path 我们使用LINGO9.0编写的FLOYD算法如下：
model:
sets:
nodes/c1..c6/;
link(nodes,nodes):w,path; !path标志短路径上走过的顶点;
endsets
data:
path=0;
w=0;
@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(w(i,j),' 10.0f')),@newline(1));
@text(mydata1.txt)=@write(@newline(1)); @text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path(i,j),' 10.0f')),@newline(1));
enddata
calc:
w(1,2)=50;w(1,4)=40;w(1,5)=25;w(1,6)=10;
w(2,3)=15;w(2,4)=20;w(2,6)=25;
w(3,4)=10;w(3,5)=20;
w(4,5)=10;w(4,6)=25;w(5,6)=55;
@for(link(i,j):w(i,j)=w(i,j)+w(j,i));
@for(link(i,j) |i#ne#j:w(i,j)=@if(w(i,j)#eq#0,10000,w(i,j))); @for(nodes(k):@for(nodes(i):@for(nodes(j):
tm=@smin(w(i,j),w(i,k)+w(k,j));
path(i,j)=@if(w(i,j)#gt# tm,k,path(i,j));w(i,j)=tm)));
endcalc
end 图&网络系列博文：
【1】图与网络模型及方法：图与网络的基本概念
【2】图&网络模型应用—最短路径问题
【3】树：基本概念与最小生成树
【4】匹配问题： 匈牙利算法 、最优指派、相等子图
【5】Euler 图和 Hamilton 图
【6】计划评审方法和关键路线法【统筹方法】：广泛地用于系统分析和项 目管理
【7】最小费用流及其求法 ：
【8】最大流问题
【9】钢管订购和运输问题