ceres学习笔记（一）

参考教程：http://www.ceres-solver.org/nnls_tutorial.html

Non-linear Least Squares(非线性最小二乘法)

Introduction

Ceres可以解决边界约束非线性最小二乘问题

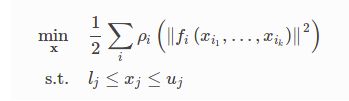
这种形式的问题出现在科学和工程的广泛领域 - 从统计学中的曲线拟合到从计算机视觉中的三维重建。

在本章中，我们将学习如何使用Ceres Solver解决（1）。 可以在示例目录中找到本章中描述的所有示例的完整工程代码。

表达式$p_i(||f_i(x_{i1},...,x_{ik})|{|}^2)$被认为残差块（ResidualBlock，$f_i(.)$叫做代价函数（CostFunction)。代价函数依赖于一系列参数$[x_{i1},...,x_{ik}]$,在大多数优化问题中，小组标量一起出现。例如，平移向量的三个分量和四元数的四个分量定义摄像机的位姿。这一系列参数（均为标量）称为参数块（parameterBlock),当然参数块中可以只是一个参数，$l_j$和$u_j$作为参数块$x_j$的边界。

$p_i$是损失函数（lossFunction),损失函数作为一个标量函数被用来减小异常值（Outliers）对非线性最小二乘问题的解的影响。

一个特殊情况是，当$p_i(x)=x$,并且范围为$l_j=-\infty$和$u_j=\infty$,我们可以得到最熟悉的非线性最小二乘问题。
$$\frac{1}{2}\sum ||f_i(x_{i1},...,x_{ik})|{|}^2$$

Hello World!

一开始，先考虑一个找到最小值函数的问题$\frac{1}{2}(10-x{)}^2$,这是一个很简单的问题，最小值位于x=10附近，但是这是一个很好用来解释基础的问题用ceres求解。

第一步编写一个函数，函数为$f(x)=10-x$

struct CostFunctor {
   template 
   bool operator()(const T* const x, T* residual) const {
     residual[0] = T(10.0) - x[0];
     return true;
   }
};

这里需要注意最重要的一点是operator()是一个模板，假设所有的输入和输出都是某种类型T,.这里使用模板允许Ceres调用CostFunctor :: operator （）， 当需要残差值时，T = double，当需要雅可比矩阵时，使用特殊类型T = Jet。这一部分在后续教程还有更详细的介绍。

一旦我们有了计算残差函数的方法，现在是时候用它来构造一个非线性最小二乘问题并让Ceres解决它。

int main(int argc, char** argv) 
{
  google::InitGoogleLogging(argv[0]);
  // The variable to solve for with its initial value.
  // 用初始值求解的变量
  double initial_x = 5.0;
  double x = initial_x;

  // Build the problem.
  // 建立问题
  Problem problem;

  // Set up the only cost function (also known as residual). This uses
  // auto-differentiation to obtain the derivative (jacobian).
  //设置唯一的成本函数（也称为残差）。 
   //这用自动微分以获得导数（雅可比）。
  CostFunction* cost_function =
      new AutoDiffCostFunction(new CostFunctor);
  problem.AddResidualBlock(cost_function, NULL, &x);

  // 进行求解
  Solver::Options options;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;
  Solver::Summary summary;
  Solve(options, &problem, &summary);

  std::cout << summary.BriefReport() << "\n";
  std::cout << "x : " << initial_x
            << " -> " << x << "\n";
  return 0;
}

AutoDiffCostFunction将CostFunctor作为输入，自动区分它并为其提供CostFunction接口。

运行程序

// Ceres Solver - A fast non-linear least squares minimizer
// Copyright 2015 Google Inc. All rights reserved.
// http://ceres-solver.org/
//
// Redistribution and use in source and binary forms, with or without
// modification, are permitted provided that the following conditions are met:
//
// * Redistributions of source code must retain the above copyright notice,
//   this list of conditions and the following disclaimer.
// * Redistributions in binary form must reproduce the above copyright notice,
//   this list of conditions and the following disclaimer in the documentation
//   and/or other materials provided with the distribution.
// * Neither the name of Google Inc. nor the names of its contributors may be
//   used to endorse or promote products derived from this software without
//   specific prior written permission.
//
// THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
// AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
// IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE
// ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE
// LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR
// CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF
// SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS
// INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN
// CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE)
// ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
// POSSIBILITY OF SUCH DAMAGE.
//
// Author: [email protected] (Keir Mierle)
//
// A simple example of using the Ceres minimizer.
//
// Minimize 0.5 (10 - x)^2 using jacobian matrix computed using
// automatic differentiation.
#include "ceres/ceres.h"
#include "glog/logging.h"
using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;
// A templated cost functor that implements the residual r = 10 -
// x. The method operator() is templated so that we can then use an
// automatic differentiation wrapper around it to generate its
// derivatives.
struct CostFunctor {
  template  bool operator()(const T* const x, T* residual) const {
    residual[0] = 10.0 - x[0];
    return true;
  }
};
int main(int argc, char** argv) {
  google::InitGoogleLogging(argv[0]);
  // The variable to solve for with its initial value. It will be
  // mutated in place by the solver.
  double x = 0.5;
  const double initial_x = x;
  // Build the problem.
  Problem problem;
  // Set up the only cost function (also known as residual). This uses
  // auto-differentiation to obtain the derivative (jacobian).
  CostFunction* cost_function =
      new AutoDiffCostFunction(new CostFunctor);
  problem.AddResidualBlock(cost_function, NULL, &x);
  // Run the solver!
  Solver::Options options;
  options.minimizer_progress_to_stdout = true;
  Solver::Summary summary;
  Solve(options, &problem, &summary);
  std::cout << summary.BriefReport() << "\n";
  std::cout << "x : " << initial_x
            << " -> " << x << "\n";
  return 0;
}

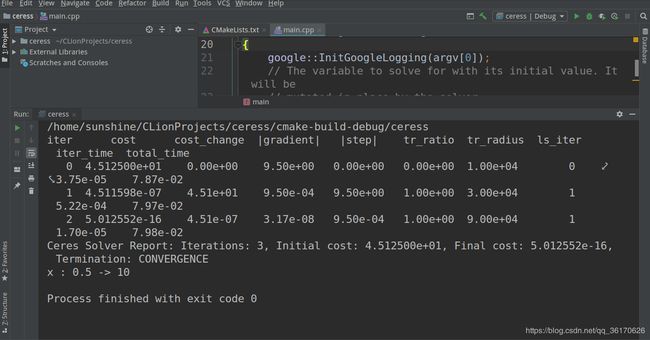
运行程序的环境 ubuntu16.04+clion

CmakeLists.txt

cmake_minimum_required(VERSION 3.5)
project(ceress)

set(CMAKE_CXX_STANDARD 11)
# 添加cmake模块以使用ceres库
list( APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake_modules )

find_package(Ceres REQUIRED)
include_directories( ${CERES_INCLUDE_DIRS} )

add_executable(ceress main.cpp)
target_link_libraries(ceress ${CERES_LIBRARIES} )

从x = 5开始，两次迭代中的求解器变为10 [2]。 细心的读者会注意到这是一个线性问题，一个线性求解应该足以得到最优值。 求解器的默认配置针对非线性问题，为简单起见，我们在此示例中未对其进行更改。 确实可以在一次迭代中使用Ceres获得该问题的解决方案。 还要注意，求解器在第一次迭代中确实非常接近0的最佳函数值。 当我们讨论Ceres的收敛和参数设置时，我们将更详细地讨论这些问题。