最小圆覆盖(经典算法【三点定圆)
刚刚学了一些基础的三维计算几何
接触到了增量法——一种看似暴力,实际睿智的算法
下面就是增量法在另一类问题上的展现
算法原文
###问题描述
给定n个点,用一个最小的圆把这些点全部覆盖,求这个圆的圆心半径
###算法
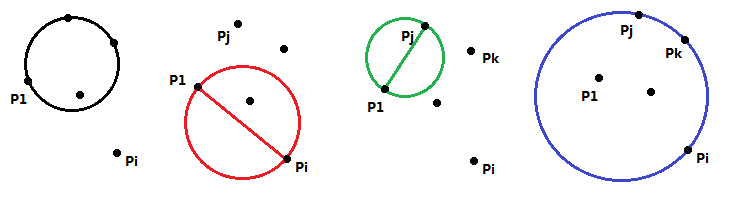
① 将所有点随机排布(这样可以保证算法的复杂度)
② 初始随意找到两点,设为 P 1 , P 2 P_1,P_2 P1,P2,以 P 1 P 2 P_1P_2 P1P2为直径得到初始圆,设为 C 2 C_2 C2( C i C_i Ci表示包含前i个点的最小圆)
③ 按顺序依次加点,设当前点为 P i P_i Pi:若 P i P_i Pi在当前圆 C i − 1 C_{i-1} Ci−1内, C i = C i − 1 C_i=C_{i-1} Ci=Ci−1;否则进入④
④ 一旦进入④,就说明我们需要在构造一个新的圆
显然插入点 P i P_i Pi一定在新圆的边界上
简单的,我们直接以 P 1 P i P_1P_i P1Pi为直径暂且得到一个 C i C_i Ci
⑤ 新得到的 C i C_i Ci不一定能包含1~i所有的点
我们找到不在 C i C_i Ci中的一点 P j ( j < i ) P_j(j
现在为止,我们能确定有两个点( P i , P j P_i,P_j Pi,Pj)在更新的圆的边界上
因此,简单的,我们直接以 P i P j P_iP_j PiPj为直径暂且得到一个 C j C_j Cj
⑥ 同样的,新得到的 C j C_j Cj不一定能包含1~j所有的点
我们找到不在 C j C_j Cj中的一点 P k ( k < j < i ) P_k(k
现在我们能确定有三个点( P i , P j , P k P_i,P_j,P_k Pi,Pj,Pk)在更新的圆的边界上
因为三点确定一个圆, P i , P j , P k P_i,P_j,P_k Pi,Pj,Pk构成了新的圆,一定能覆盖前 i i i个点
于是,这个问题就被转化为若干个子问题来求解了
由于三个点确定一个圆,我们的过程大致上做的是从没有确定点,到有一个确定点,再到有两个确定点,再到有三个确定点来求圆的工作
###小细节
####Q1.
过三点如何求圆?
####A1.
先求叉积
若叉积为0,即三个点在同一直线,那么找到距离最远的一对点,以它们的连线为直径做圆即可;
若叉积不为0,即三个点不共线,那么就求三角形的外接圆
####Q2.
如何求三角形外接圆?
####A1.
设三个点 ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) (x_1,y_1),(x_2,y_2),(x_3,y_3) (x1,y1),(x2,y2),(x3,y3)
设过 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) (x1,y1),(x2,y2)的直线 l 1 l_1 l1方程为 A x + B y = C Ax+By=C Ax+By=C
它的中点为 ( x m i d , y m i d ) = ( x 1 + x 2 2 , y 1 + y 2 2 ) (x_{mid},y_{mid})=({x_1+x_2 \over 2},{y_1+y_2 \over 2}) (xmid,ymid)=(2x1+x2,2y1+y2)
方法一:
l 1 l_1 l1中垂线方程为 A 1 x + B 1 y = C 1 A_1x+B_1y=C_1 A1x+B1y=C1
则它的中垂线方程中:
A 1 = − B = x 2 − x 1 A_1=-B=x_2-x_1 A1=−B=x2−x1
B 1 = A = y 2 − y 1 B_1=A=y_2-y_1 B1=A=y2−y1
C 1 = − B ∗ x m i d + A ∗ y m i d = ( x 2 2 − x 1 2 ) + ( y 2 2 − y 1 2 ) 2 C_1=-B*x_{mid}+A*y_{mid}={(x_2^2-x_1^2)+(y_2^2-y_1^2) \over 2} C1=−B∗xmid+A∗ymid=2(x22−x12)+(y22−y12)
方法二:
如果我们把直线用“点+向量”的形式记录,求中垂线就简单多了
旋转原直线方向向量九十度即可
向量旋转
x’=xcosθ-ysinθ
y’=xsinθ+ycosθ
同理可以知道过 ( x 1 , y 1 ) , ( x 3 , y 3 ) (x1,y1),(x3,y3) (x1,y1),(x3,y3)的直线的中垂线的方程
于是这两条中垂线的交点就是圆心
####Q3.
如何求两条直线交点?
####A3.
方法一:
设两条直线为 A 1 x + B 1 y = C 1 A_1x+B_1y=C_1 A1x+B1y=C1和 A 2 x + B 2 y = C 2 A_2x+B_2y=C_2 A2x+B2y=C2
求 d e l t a = A 1 ∗ B 2 − A 2 ∗ B 1 delta=A_1*B_2-A_2*B_1 delta=A1∗B2−A2∗B1(类似叉积)
如果 d e l t a = 0 delta=0 delta=0,说明两直线平行;
若不等于0,则求交点: x = B 2 ∗ C 1 − B 1 ∗ C 2 d e l t a , y = A 1 ∗ C 2 − A 2 ∗ C 1 d e l t a x={B2*C1 -B1*C2 \over delta},y={A1*C2-A2*C1 \over delta} x=deltaB2∗C1−B1∗C2,y=deltaA1∗C2−A2∗C1
方法二:
如果我们把直线用“点+向量”的形式记录,这个问题也很简单
node jiao(node p,node v,node q,node w)
//p+tv
//q+tw
{
node u=p-q;
double t=Cross(w,u)/Cross(v,w);
return p+v*t;
}
###Code
思路基本上就是这样,代码实现可能不是这么显然
瞧好了您内
const double Pi=acos(-1.0);
int dcmp(double x)
{
if (fabs(x)0) //不在圆内
{
c=P[i],r=0;
for (int j=1;j0)
{
c=(P[i]+P[j])/2.0;
r=lenth(c-P[i]);
for (int k=1;k0)
{
c=get_c(P[i],P[j],P[k]);
r=lenth(c-P[i]);
}
}
}
}