Tarjan算法

中考前最后一篇博客啦~

---

之前就一直听说过Tarjan算法（在图论区），但是一直都不知道到底是个什么，应该怎么用，这篇博客就来讲一讲Tarjan算法是个什么东西

---

Tarjan算法

一些前置知识

1.连通：若在无向图中，任意两个点都可以间接或直接连接，则这个图连通

2.强连通：在有向图中，任意两个点都可以间接或直接连接，则这个图强连通

3.弱连通：刚刚说了强连通是在有向图中，这里指的是在有向图中，把它强行看成是无向图，如果任意两个点都可以间接或直接连接，则这个图弱连通

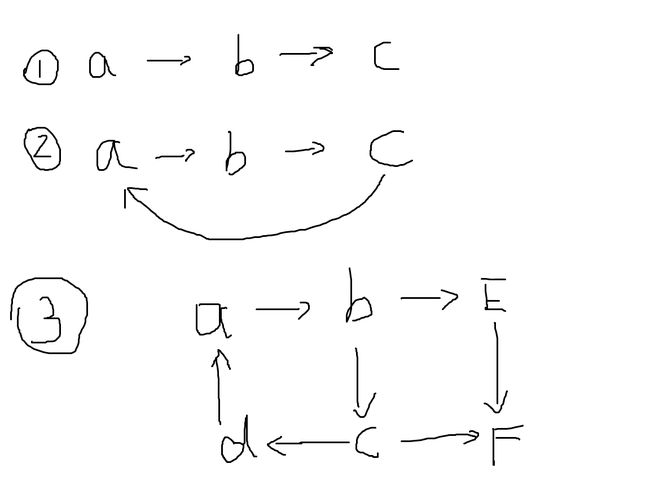
好了，以上的知识了解就行，并不会太多提及，重点还是强连通分量这个东西。刚刚说了强连通是在整个图中的，那么我们可以在整个图中找到一些小部分的强连通子图，这就叫做强连通分量，画图来理解：

其中图①就是一个非强连通图，图②就是一个强连通图

图③中有3个强连通分量，其中{ \({A,B,C,D}\) }为1个强连通分量，{ \({E}\) }为一个强连通分量，{ \({F}\) }

基本概念

这是一个基于DFS深度搜索的算法，我们用一个二元组 \(i \space(xu,low)\) 来表示节点i的一些信息，其中\(xu\)表示\(i\)是第几个被搜索到的，\(low\)表示这个节点最早在什么时候被找到,那么我们模拟一下一张图的过程（因为电脑画图太难啦，但是字迹有点丑，emmm将就一下吧）：

对于上面的图，我们就可以确定三个强连通分量，但是可能有点描述不清楚

我们对于一个点一直向下找，并存入栈中，记录它的\(xu\)和\(low\)，并标记这个点已经被寻找过，如果你的下一个点被找过并且还在栈中，那么就可以更新当前这个点的\(low\)。当一个点的\(xu\)和\(low\)相等时，说明这是一个强连通分量，就将这一个强连通分量全部从栈中弹出。持续进行这一个操作，直到所有点都被搜过

强烈推荐这个视频，讲得真的非常好，视频模拟以上的过程简单易懂（不是我的）

传送门

int ans;
bool in[MAXN]; //in表示是否在栈中 
int xu[MAXN],low[MAXN]; //搜索的顺序和最开始被发现的时间 
int tim; //记录时间 
int q[MAXN],top; //手动模拟栈 
for(register int i=1;i<=n;i++){
	if(!low[i]) tarjan(i); //对每一个没被找过点进行处理 
}
void tarjan(int s){
	xu[s]=low[s]=++tim;  //先初始化当前点 
	q[++top]=s; //入栈 
	in[s]=true; //在栈中 
	for(register int i=head[s];i;i=e[i].net){
		int y=e[i].to; //找下一个点 
		if(xu[y]==false){ //没找过 
			tarjan(y); //继续 
			low[s]=min(low[s],low[y]); //比较一下 
		}else if(in[y]==true){ //在栈中 
			low[s]=min(low[s],xu[y]); //更新 
		}
	}
	if(low[s]==xu[s]){
		ans++; //强连通分量的数量++ 
		while(q[top]!=s){
			in[q[top]]=false;
			top--;
		}
		in[q[top]]=false;
		top--;//将这个强连通分量全部弹出 
	}
}

这就是一个Tarjan算法的模板吧，但是我并没有找到一个裸的强连通分量的题，但是强连通分量往往会涉及到另外一个东西——缩点

缩点

缩点简单来说，就是将图中的强连通分量全部转化为一个点来表示，这样转化的结果就是将之前的有向有环图转化成了一个有向无环图，而这个被压缩的强连通分量应该存储所有点的信息

如图（是不是生动形象）：

我们只对强连通分量进行缩点，虽然图中有三个强连通分量，但是因为前面两个孤立的点不太好表示，但是要知道这也是被压缩之后的

那么在Tarjan中已经知道了如何求出每一个强连通分量，也可以非常方便的记录每一个点到底属于哪一个强连通分量，那么将这个强连通分量压缩成点之后，如何还原这个图呢？

其实很简单，对于上面的图，我们有三个强连通分量，那么挨着编个号，在另外用一个邻接表存储就可以了，但是压缩成点之后一定记得记录每一个点的信息

这里就用两到例题直接来讲吧

P3387 【模板】缩点

这道题就是一个非常经典的缩点（不然为什么是模板题），我们将每一个强连通分量压缩为一个点，这个点的点权就是所有在这一个强连通分量中的点的点权之和，然后再在新建的被压缩之后图上跑各种神奇的算法，例如拓扑排序，记忆化搜索等

#include
using namespace std;
const int MAXN=5e5+5;
int n,m;
struct node{
	int net,to,w;
}e[MAXN],e2[MAXN];
int head[MAXN],tot;
void add(int x,int y){
	e[++tot].net=head[x];
	e[tot].to=y;
	head[x]=tot;
}//用来存储原来的图 
int head2[MAXN],tot2;
void add_s(int x,int y){
	e2[++tot2].net=head2[x];
	e2[tot2].to=y;
	head2[x]=tot2;
}//存储压缩之后的图 
int ans;
bool in[MAXN]; 
int xu[MAXN],low[MAXN]; 
int tim;
int q[MAXN],top;
int suo[MAXN],d[MAXN],a[MAXN]; //suo表示这个点属于哪一个强连通分量，d表示这个压缩之后的强连通分量的点权，a就是每个点的点权 
int f[MAXN]; //记忆化搜索 
void tarjan(int s){
	xu[s]=low[s]=++tim;
	q[++top]=s;
	in[s]=true;
	for(register int i=head[s];i;i=e[i].net){
		int y=e[i].to;
		if(xu[y]==false){
			tarjan(y);
			low[s]=min(low[s],low[y]);
		}else if(in[y]==true){
			low[s]=min(low[s],xu[y]);
		}
	}
	if(low[s]==xu[s]){
		ans++;
		while(q[top]!=s){
			in[q[top]]=false;
			suo[q[top]]=ans; //记录属于哪一个强连通分量 
			d[ans]+=a[q[top]]; //权值累计 
			top--;
		}
		suo[q[top]]=ans;
		in[q[top]]=false;
		d[ans]+=a[q[top]];
		top--; 
	}
}
void dfs(int x){
	if(f[x]) return ;
	int sum=0;
	f[x]=d[x];
	for(register int i=head2[x];i;i=e2[i].net){
		int y=e2[i].to;
		dfs(y);
		sum=max(sum,f[y]);
	}
	f[x]+=sum;
} //记忆化搜索记录最大值 
int main(){
	scanf("%d%d",&n,&m);
	for(register int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(register int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);
	}
	for(register int i=1;i<=n;i++){
		if(!low[i]) tarjan(i);
	} //找强连通分量 
	for(register int x=1;x<=n;x++){
		for(register int i=head[x];i;i=e[i].net){
			int y=e[i].to;
			if(suo[x]!=suo[y]) add_s(suo[x],suo[y]);
		}
	}//这一坨就是连接将所有强连通分量缩点之后，再进行建图 
	int maxx=0;
	for(register int i=1;i<=ans;i++){
		dfs(i);
		maxx=max(maxx,f[i]);
	}//记录一下最大值 
	printf("%d",maxx);
	return 0;
}

P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G

这就是传说中的爱屋及乌吗

首先对于喜欢的牛，就相当于可以建一条有向边，那么对于一群相互喜欢的牛就是一个强连通分量，然后进行缩点建边，当一个强连通分量出度为0的时候，说明所有的牛都喜欢他们，那么这一个强连通分量中的所有牛都是明星

特别地，当一个图中存在两个及两个以上的出度为0的强连通分量时，说明不可能有一些奶牛被所有人喜欢，这个时候特判答案为0

#include
using namespace std;
const int MAXN=5e5+5;
int n,m;
struct node{
	int net,to,w;
}e[MAXN],e2[MAXN];
int head[MAXN],tot;
void add(int x,int y){
	e[++tot].net=head[x];
	e[tot].to=y;
	head[x]=tot;
}
int head2[MAXN],tot2;
void add_s(int x,int y){
	e2[++tot2].net=head2[x];
	e2[tot2].to=y;
	head2[x]=tot2;
} //还是老样子 
int ans;
bool in[MAXN];
int xu[MAXN],low[MAXN];
int tim;
int q[MAXN],top;
int suo[MAXN],d[MAXN],a[MAXN];
void tarjan(int s){
	xu[s]=low[s]=++tim;
	q[++top]=s;
	in[s]=true;
	for(register int i=head[s];i;i=e[i].net){
		int y=e[i].to;
		if(xu[y]==false){
			tarjan(y);
			low[s]=min(low[s],low[y]);
		}else if(in[y]==true){
			low[s]=min(low[s],xu[y]);
		}
	}
	if(low[s]==xu[s]){
		ans++;
		while(q[top]!=s){
			in[q[top]]=false;
			suo[q[top]]=ans;
			d[ans]+=a[q[top]];
			top--;
		}
		suo[q[top]]=ans;
		in[q[top]]=false;
		d[ans]+=a[q[top]];
		top--;
	}
}//和之前那个缩点的程序一模一样 
int main(){
	scanf("%d%d",&n,&m);
	for(register int i=1;i<=n;i++) a[i]=1; //注意每头牛的权值都为1 
	for(register int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);
	}
	for(register int i=1;i<=n;i++){
		if(!low[i]) tarjan(i);
	}
	int maxx=0; 
	int pp[MAXN];
	for(register int x=1;x<=n;x++){
		for(register int i=head[x];i;i=e[i].net){
			int y=e[i].to;
			if(suo[x]!=suo[y]) {
				add_s(suo[x],suo[y]);
				pp[suo[x]]++; //出度增加 
			}
		}
	}
	int kk=0; //记录有多少出度为 0的强连通分量 
	for(register int i=1;i<=ans;i++){
		if(pp[i]==0) maxx+=d[i],kk++; //累加答案 
	}
	if(kk==1)printf("%d",maxx);
	else puts("0");
	return 0;
}

那么Tarjan算法就差不多讲完了，但是Tarjan算法有很多的扩展延伸的空间，可以进行很多操作，但是蒟蒻还没有学习，如果学了会继续更新的，如果还有不懂的，或者是我没有讲到，讲懂的地方，欢迎提问，也可以借助其他dalao的博客进行学习