支持向量机(SVM) | SMO算法实现

01 起

在统计学习方法|SVM这篇文章中，我们学习了支持向量机的原理和理论上的算法实现，我们一起回忆一下，支持向量机可以处理三种类型的数据：

1. 线性可分支持向量机——求解策略，硬间隔最大化
2. 线性支持向量机——求解策略，软间隔最大化
3. 非线性支持向量机——求解策略，核技巧+软间隔最大化

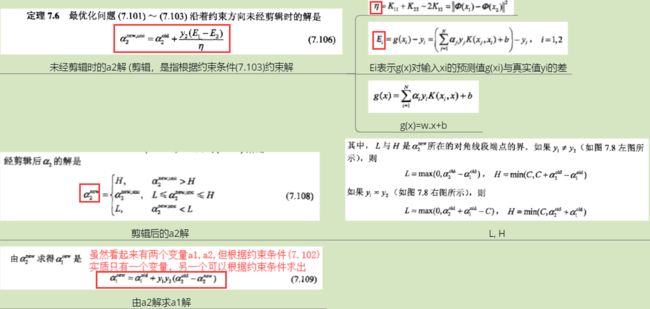
我们提出一个问题

当数据量很大时，以上提出的算法求解复杂度呈指数上升，算法会变得十分低效，该怎么办呢？

我们给出了解法思路

在对偶问题中，每次只求解优化两个alpha的值，如此遍历求解的方法与一次求解所有alpha的方法得到的结果是完全一致的。

其实这就是SMO(序列最小优化算法)的原理，今天我们将基于SMO原理，自己写一个代码来实现SMO算法。

---

02 SMO算法原理

在统计学习方法中，给出SMO算法思路如下：

我们可以将SMO算法过程归纳如下：

1. 初始化所有变量的解ai=0
2. 选取优化变量a1,a2，解析求解这两个变量的二次规划问题，得到最优解a1’,a2’
3. 验证，所有变量的解ai是否满足KKT条件，若不满足，继续step2，否则step4
4. 得到a=a1’,a2’…

SMO算法求解的是对偶问题的解alpha，在得到alpha值后，可以通过下面的公式求出参数向量w和常数项b，从而得到分离超平面

SMO算法有两个关键点：

• 选择两个alpha进行优化
• 求解所选alpha的解析解

其中，

• 选择第一个alpha(a1)我们称之为外循环，选择原则是违反KKT条件最严重的点(SMO算法在，选择足够违反(>toler)KKT条件的样本点)，选择第二个alpha(a2)为内循环，选择原则是与a1变化相反的点(E1-E2最大的样本点)

• 求解a1,a2解析解的问题，就是两个变量的二次规划问题，可以通过一下公式求得
  

下面我们基于python3实现算法！

---

03 辅助函数

辅助函数包括，

• 数据加载函数
• 根据alphai的i随机选择j的函数
• 根据L H边界值剪切alpha的函数
• 根据alpha计算w的函数
• 绘图函数

def loadDataSet(filename):
    #filename是待读取文件的文件名或路径+文件名
    dataMat=[];labelMat=[]
    fr=open(filename)
    for line in fr.readlines():
        lineArr=line.strip().split("\t")
        dataMat.append([float(lineArr[0]),float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat

def randPickj(i,m):
    #i是alphai的i值，整数; m是alpha个数; j不能等于i
    j=i
    while j==i:
        j=int(np.random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):
    if aj>H:
        aj=H
    if aj<L:
        aj=L
    return aj

根据alpha计算w的函数

def weight(data,label,alphas):
    dataMatrix=np.mat(data);labelMatrix=np.mat(label).transpose() #这里labelMatrix形状为m*1
    m,n=dataMatrix.shape
    w=np.mat(np.zeros((1,n))) #初始化w，为1行n列的全零矩阵，n为data维度数
    
    """w=求和(ai*yi*xi),求和对象是支持向量，即，ai>0的样本点，xi，yi为支持向量对应的label和data"""
    for i in range(m):
        if alphas[i]>0:
            w+=labelMatrix[i]*alphas[i]*dataMatrix[i,:]
    return w.tolist()

绘图函数

"""
绘制样本数据以及决策边界
思路：
1. 将样本数据根据样本类别标签labelMat分别放入不同的坐标集中
2. 根据坐标集合，分别绘制两个类别样本的散点图
3. 决策边界即x2=f(x1),由w1*x1+w2*x2+b=0得到x2(即y=(-b-w1x1)/w2)
"""
def plotBestFit(weights,b,filename):
    dataMat,labelMat=loadDataSet(filename) #加载样本特征、样本类别
    dataArr=np.array(dataMat)
    n=dataArr.shape[0] #n个样本
    xcord1=[];ycord1=[]
    xcord2=[];ycord2=[] #两个类别的样本的xy坐标值，x对应x1,y对应x2
    
    #将样本数据根据样本类别标签labelMat分别放入不同的坐标集中
    for i in range(n):
        if int(labelMat[i])==1: #第i个样本是1类
            xcord1.append(dataArr[i,0]) #第i个样本的x1值
            ycord1.append(dataArr[i,1]) #第i个样本的x2值
        else:
            xcord2.append(dataArr[i,0]) #第i个样本的x1值
            ycord2.append(dataArr[i,1]) #第i个样本的x2值
    
    #绘制两类样本的散点图
    fig=plt.figure(figsize=(12,8))
    plt.scatter(xcord1,ycord1,c="red",s=50,label="label=1")
    plt.scatter(xcord2,ycord2,c="blue",s=50,label="label=-1") #继续在原图上作图
    
    #绘制决策边界
    x=np.arange(-3.0,5.0,0.1)
    y=(-b-weights[0][0]*x)/weights[0][1] #由w1*x1+w2*x2+b=0得到x2(即y)=(-b-w1x1)/w2
    x.shape=(len(x),1);y.shape=(len(x),1) 
    plt.plot(x,y,color="darkorange",linewidth=3.0,label="Boarder") #继续在ax图上作图
    
    plt.xlabel("X1",fontsize=16)
    plt.ylabel("X2",fontsize=16)
    plt.title("SMO BestFit",fontsize=20,fontweight="bold")
    plt.legend() #添加图标注解
    plt.show()

---

04 简化版SMO算法

说明：

• 简化部分在于省去了选择alphai的外循环过程，省去了更新Ei的过程
• 写这个算法的目的在于深入理解SMO算法过程

4.1 代码

def SMOsimple(data,label,C,toler,maxIter):
    """
    data:样本各属性值
    label：各样本对应标签
    C：软间隔最大化的松弛系数对应的惩罚因子，也是约束条件中alpha的上界(对于线性可分数据集，C作用不大；对于线性不可分数据集，结果对C敏感)
    toler：容错率，偏离KKT条件的容错率
    maxIter：外层循环迭代次数
    """
    #初始化alpha=0,b=0,alpha个数为样本数，一个样本对应一个alpha
    dataMatrix=np.mat(data);labelMatrix=np.mat(label).transpose() #这里labelMatrix形状为m*1
    b=0;m,n=dataMatrix.shape
    alphas=np.mat(np.zeros((m,1)))
    
    iters=0
    while iters<maxIter:
        alphaPairsChanged=0 #存储每次内循环改变的aplha对数量，每次外循环应该重新置零
        for i in range(m): #内循环遍历所有样本点
            
            #计算第i个样本点的预测值gxi和预测误差Ei
            gxi=float(np.multiply(alphas,labelMatrix).transpose()*(dataMatrix*dataMatrix[i,:].transpose()))+b
            Ei=gxi-labelMatrix[i]
            
            """检验第i个样本点是否满足KKT条件，若满足则会跳出本次内循环(不更新这个alphai)，进行下一次内循环；
            若不满足，看它是否是违反KKT条件超过容错率toler的点,若不是，则跳出本次内循环(不更新这个alphai)，进行下一次内循环；
            若是，则继续选择alphaj，计算gx,E,eta,进而求得aj解析解，进而求得ai解析解，进而更新b值"""
            if (labelMatrix[i]*Ei<-toler and alphas[i]<C) or (labelMatrix[i]*Ei>toler and alphas[i]>0):
                j=randPickj(i,m)
                gxj=float(np.multiply(alphas,labelMatrix).transpose()*(dataMatrix*dataMatrix[j,:].transpose()))+b
                Ej=gxj-labelMatrix[j]
                
                #存储alpha初始值，用于后续计算
                alphaIold=alphas[i].copy()
                alphaJold=alphas[j].copy()
                
                #计算剪切边界(很简单的几何计算，见统计学习方法)
                if labelMatrix[i]!=labelMatrix[j]:
                    L=max(0,alphas[j]-alphas[i]) #这里alpha[i]仍然等于alphaIold
                    H=min(C,C+alphas[j]-alphas[i])
                else:
                    L=max(0,alphas[j]+alphas[i]-C)
                    H=min(C,alphas[j]+alphas[i])
                if L==H:
                    print ("L==H")
                    continue #第一个跳出条件(跳出本次内循环，遍历下一个alpha进行更新)
                
                #计算eta
                eta=dataMatrix[i,:]*dataMatrix[i,:].transpose()+dataMatrix[j,:]*dataMatrix[j,:].transpose()\
                -2.0*dataMatrix[i,:]*dataMatrix[j,:].transpose()
                if eta==0:
                    print ("eta=0")
                    continue #第二个跳出条件(因为eta=0不好处理，且出现情况较少，因此这里咱不处理，直接跳出)
                    
                #根据统计学习方法中的结果公式得到alphaj的解析解
                alphas[j]=alphas[j]+labelMatrix[j]*(Ei-Ej)/eta
                alphas[j]=clipAlpha(alphas[j],H,L)
                
                #检验alphaj与alphaJold是否有足够大的改变，若改变不够大，说明与alpha旧值没有什么差异，跳出本次内循环
                if alphas[j]-alphaJold<0.00001:
                    print ("j not moving enough")
                    continue #第三个跳出条件
                    
                #约束条件让我们可以根据alphaJ求出alphaI
                alphas[i]=alphas[i]+labelMatrix[i]*labelMatrix[j]*(alphaJold-alphas[j])
                
                #更新b值,根据alpha是否在0～C决定更新的b值
                b1=-Ei-labelMatrix[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].transpose()\
                -labelMatrix[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[i,:].transpose()+b
                
                b2=-Ej-labelMatrix[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].transpose()\
                -labelMatrix[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].transpose()+b
                
                #若ai或aj在(0,C)之间，则取b=bi或b=bj，若ai aj都不在(0,C)之间，取均值
                if alphas[i]>0 and alphas[i]<C:
                    b=b1
                elif alphas[j]>0 and alphas[j]<C:
                    b=b2
                else:
                    b=(b1+b2)/2.0
                alphaPairsChanged+=1 #若进行到这里，说明ai aj经过了层层筛选(continue)，已经被更新，于是内循环中alpha对更新次数+1
                print ("iter:{0}; i:{1}; alpha pair changed:{2}".format(iters,i,alphaPairsChanged))
            
        """只有在内循环未对任何一对alpha做修改时，iters+1；否则我们让iters回到0，继续内循环；
        只有当内循环未修改任一alpha对，且连续maxIter次迭代，才会结束(以保证所有alpha得到了充分的修改)
        (这里其实有个改进点：只要alpha被修改，iter就+1，然后在引入一个停止条件(整个数据集没有可以再更新的alpha值)同时判断即可)
        注意缩进"""
        if alphaPairsChanged==0:
            iters+=1
        else:
            iters=0
        print ("iteration numer:%d" %iters)
    return b,alphas

4.2 测试

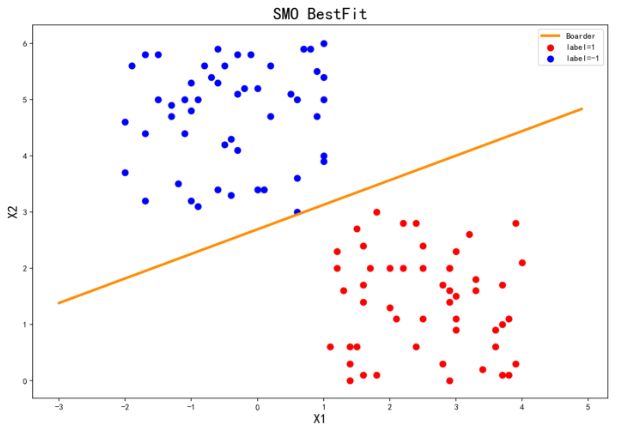
我们用一个线性可分的数据集进行测试，数据集共100个样本点，结果如下(线性不可分数据集也进行了测试，效果良好，篇幅限制，这里只展示线性可分数据集的测试结果)

dataMat1,labelMat1=loadDataSet("SMO_data2.txt") #SMO_data2.txt是线性可分数据集
start=time.time()
b1,alphas1=SMOsimple(dataMat1,labelMat1,0.6,0.001,100)
print ("\n","time used:.{0}s".format(time.time()-start))
w1=weight(dataMat1,labelMat1,alphas1)
plotBestFit(w1,b1,"SMO_data2.txt")

简化版SMO算法用时8.67s完成优化

得到的分离超平面如下：

---

05 完整版SMO算法

在简化版的SMO算法测试中，虽然我们只使用了100个样本点进行测试，但算法也用了8.67s才完成优化，如果是体量更加巨大的数据集，算法效率将十分低下！

**怎么办呢？完整版算法来解决！**相比于简化版，完整版优化了：

• 外循环中用启发方法选择ai：在全集遍历循环和边界遍历循环中切换搜索违反KKT条件超过容错率toler的点
  1. 先遍历全集，若全集遍历中未修改任何alpha，说明alpha均满足KKT条件，循环停止；
  2. 若全集遍历中修改了alpha值，则在下一轮循环进入边界遍历(边界指0
  3. 在边界遍历中，修改边界点的alpha，直到无alpha可修改(此时alphaPairChanged=0)，再次进入全集遍历；
  4. 如此循环往复，直到全集遍历中未修改任何alpha，循环停止
• 内循环中通过选择相较ai具有最大步长(即Ei-Ej)的aj
• 每次修改ai aj后，紧跟着修改Ei Ej

5.1 代码

完整版辅助函数
包括，计算Ei的函数、选择相较ai具有最大步长(即Ei-Ej)的aj的函数、更新Ei矩阵的函数

class optStruct:
    def __init__(self,data,label,C,toler):
        #全局变量
        self.X=data
        self.labelMatrix=label
        self.C=C
        self.toler=toler
        self.m=data.shape[0] #m为样本数
        
        #初始化alpha矩阵、b、Es矩阵
        self.alphas=np.mat(np.zeros((self.m,1)))
        self.Es=np.mat(np.zeros((self.m,2))) #缓存误差，两列，第一列表示当前Ei是否有效，第二列表示当前的Ei值
        self.b=0
    
def calcEk(oS,k):
    gxk=float(np.multiply(oS.alphas,oS.labelMatrix).transpose()*(oS.X*oS.X[k,:].transpose()))+oS.b
    Ek=gxk-float(oS.labelMatrix[k])
    return Ek
    
#选择相较ai具有最大步长(即Ei-Ej)的aj的函数
def selectJ(oS,i,Ei):
    maxK=-1;maxDeltaE=0;Ej=0 #DeltaE表示Ei-Ej,k表示DeltaE最大的样本点索引值，最终会将Ek赋值给Ej
    oS.Es[i]=[1,Ei] #使Es矩阵第i位有效
    validEsList=np.nonzero(oS.Es[:,0].A)[0] #将Es矩阵中有效的Ei对应的索引值选出来，作为挑选j的池子
        
    if len(validEsList)>1:
        for k in validEsList:
            if k==i:
                continue
            Ek=calcEk(oS,k)
            deltaE=abs(Ei-Ek)
            if deltaE>maxDeltaE:
                maxDeltaE=deltaE;maxK=k;Ej=Ek
        return maxK,Ej
    else: #若validEsList只有一个Ei有效(初次循环)，则随机选取一个j
        j=randPickj(i,oS.m)
        Ej=calcEk(oS,j)
    return j,Ej
    
def updateEk(oS,k):
    Ek=calcEk(oS,k)
    oS.Es[k]=[1,Ek]

内循环

• 外循环是对ai的循环，内循环是在ai选定的基础下对aj的循环
• 代码和逻辑与SMO简化版相似(因为简化版SMO未对外循环做任何优化)

def innerL(i,oS):
    Ei=calcEk(oS,i)
    
    #判断Ei是否是违反KKT条件超过toler的点，若是再继续挑选j
    if (oS.labelMatrix[i]*Ei<-oS.toler and oS.alphas[i]<oS.C) or (oS.labelMatrix[i]*Ei>oS.toler and oS.alphas[i]>0):
        j,Ej=selectJ(oS,i,Ei)
        alphaIold=oS.alphas[i].copy();alphaJold=oS.alphas[j].copy()
        
        #计算L，H
        if oS.labelMatrix[i]!=oS.labelMatrix[j]:
            L=max(0,oS.alphas[j]-oS.alphas[i]) #这里alpha[i]仍然等于alphaIold
            H=min(oS.C,oS.C+oS.alphas[j]-oS.alphas[i])         
        else:
            L=max(0,oS.alphas[j]+oS.alphas[i]-oS.C)
            H=min(oS.C,oS.alphas[j]+oS.alphas[i])
        if L==H:
            print ("L==H")
            return 0 #第一个跳出条件(跳出本次内循环，遍历下一个alpha进行更新)
        
        #计算eta
        eta=oS.X[i,:]*oS.X[i,:].transpose()+oS.X[j,:]*oS.X[j,:].transpose()-2.0*oS.X[i,:]*oS.X[j,:].transpose()
        if eta==0:
            print ("eta=0")
            return 0 #第二个跳出条件(因为eta=0不好处理，且出现情况较少，因此这里咱不处理，直接跳出)
                    
        #根据统计学习方法中的结果公式得到alphaj的解析解，并更新Ej值
        oS.alphas[j]=oS.alphas[j]+oS.labelMatrix[j]*(Ei-Ej)/eta
        oS.alphas[j]=clipAlpha(oS.alphas[j],H,L)
        updateEk(oS,j) #更新Ej值
        
        #检验alphaj与alphaJold是否有足够大的改变，若改变不够大，说明与alpha旧值没有什么差异，跳出本次内循环
        if abs(oS.alphas[j]-alphaJold)<0.00001:
            print ("j not moving enough")
            return 0 #第三个跳出条件
                    
        #约束条件让我们可以根据alphaJ求出alphaI
        oS.alphas[i]=oS.alphas[i]+oS.labelMatrix[i]*oS.labelMatrix[j]*(alphaJold-oS.alphas[j])
        updateEk(oS,i) #更新Ei值
        
        #更新b值,根据alpha是否在0～C决定更新的b值
        b1=-Ei-oS.labelMatrix[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].transpose()\
        -oS.labelMatrix[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[i,:].transpose()+oS.b
                
        b2=-Ej-oS.labelMatrix[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].transpose()\
        -oS.labelMatrix[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].transpose()+oS.b
                
        #若ai或aj在(0,C)之间，则取b=bi或b=bj，若ai aj都不在(0,C)之间，取均值
        if oS.alphas[i]>0 and oS.alphas[i]<oS.C:
            oS.b=b1
        elif oS.alphas[j]>0 and oS.alphas[j]<oS.C:
            oS.b=b2
        else:
            oS.b=(b1+b2)/2.0
        return 1 #若执行到这里都没有return0跳出，说明已经完成了一个alpha对的更新，返回一个1
    
    else:
        return 0 #若ai不足够违反KKT条件，则return0跳出本次内循环

外循环

• 简化版未对外循环做任何操作，这是完整版SMO与简化版的差异之一
• 外循环选择ai的i的逻辑：遍历全集，若全集无修改alpha对，则说明alpha已符合要求，循环停止；否则下一轮进入边界遍历修改alpha对，直到边界遍历中再无alpha对可修改；则下一轮进入全集遍历，如此循环往复寻找ai，直到全集无修改alpha对时停止

def SMOpro(data,label,C,toler,maxIter,kTup=("lin",0)):
    oS=optStruct(np.mat(data),np.mat(label).transpose(),C,toler)
    iter=0;entireSet=True;alphaPairsChanged=0
    
    #当迭代次数达到上限(这里的迭代次数只要完成一次循环遍历就+1，不论该次循环遍历是否修改了alpha对)，或全集再无可修改的alpha对时，循环停止，计算完成
    while (iter<maxIter) and (entireSet or alphaPairsChanged>0):
        alphaPairsChanged=0
        if entireSet: #全集遍历
            for i in range(oS.m):
                alphaPairsChanged+=innerL(i,oS)
                print ("fullset, iter:%d i:%d, pairsChanged: %d" %(iter,i,alphaPairsChanged))
            iter+=1 #这里的迭代次数只要完成一次循环遍历就+1，不论该次循环遍历是否修改了alpha对
        
        else: #边界遍历
            boundIs=np.nonzero((oS.alphas.A>0)*(oS.alphas.A<oS.C))[0] #选择0
            for i in boundIs:
                alphaPairsChanged+=innerL(i,oS)
                print ("bound, iter:%d i:%d, pairsChanged: %d" %(iter,i,alphaPairsChanged))
            iter+=1
            
        #控制遍历往返于全集遍历和边界遍历
        if entireSet:
            entireSet=False #若本轮是全集遍历，则下一轮进入边界遍历(下一轮while条件中的entire是False)
        elif alphaPairsChanged==0:
            entireSet=True  #若本轮是边界遍历，且本轮遍历未修改任何alpha对，则下一轮进入全集遍历
        print ("iteration number: %d" %iter)
    return oS.b,oS.alphas

5.2 测试

使用与简化版SMO同样的测试数据集进行测试

data3,label3=loadDataSet("SMO_data2.txt")
start=time.time()
b3,alphas3=SMOpro(data3,label3,0.6,0.001,60)
print ("\n","time used:.{0}s".format(time.time()-start))
w3=weight(data3,label3,alphas3)
plotBestFit(w3,b3,"SMO_data2.txt")

时间效率相比简化版提升了40+倍！

得到的分离超平面如下，对比简化版的分离超平面，分离得好像更好呢：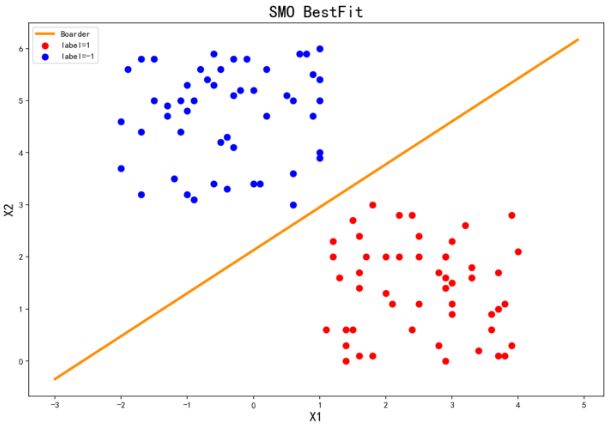

---

06 总结

本文介绍了支持向量机SMO的算法原理，然后基于算法原理，利用python3实现了SMO简化版/完整版算法，旨在深刻理解 SVM原理，SMO过程，希望对你有帮助。

下一期准备尝试用SVM算法分类非线性数据集，敬请期待~

---

07 参考

1. 《统计学习方法》 李航 Chapter7
2. 《机器学习实战》 Peter Harrington Chapter6