视觉SLAM中的李群与李代数

写在前面

首先声明，这篇博客只是高博的《视觉SLAM十四讲》的学习笔记，稍加一些自己的领悟和思考。如果想系统和详细的学习李群与李代数，强烈建议移步。

为什么要使用李群和李代数

三维世界中刚体运动的描述方式，包括旋转矩阵、旋转向量、欧拉角、四元数等若干种方式。在SLAM 中，除了旋转表示之外，还要对它们进行估计和优化。因为在SLAM 中位姿是未知的，而我们需要解决什么样的相机位姿最符合当前观测数据这样的问题。一种典型的方式是把它构建成一个优化问题，求解最优的$R,t$，使得误差最小化。

而旋转矩阵自身是带有约束的（正交且行列式为1）。它们作为优化变量时，会引入额外的约束，使优化变得困难。通过李群——李代数间的转换关系，我们希望把位姿估计变成无约束的优化问题，简化求解方式。

群

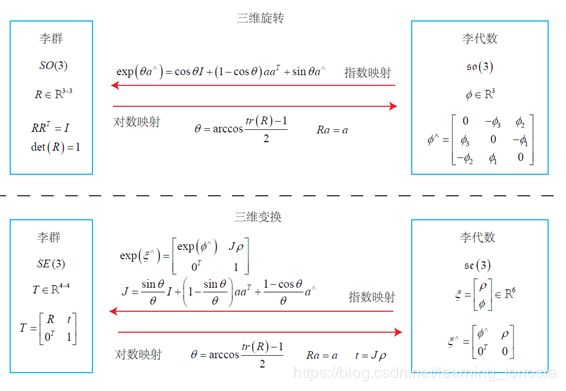
三维旋转矩阵构成了特殊正交群$SO(3)$
$$SO(3)=\{R\in {\mathbb{R}}^{3\times 3}|R{R}^T=I,det(R)=1\}$$
三维变换矩阵构成了特殊欧式群$SE(3)$
$$SO(3)=\{T=\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]\in {\mathbb{R}}^{4\times 4}|R\in SO(3),t\in {\mathbb{R}}^3\}$$
注：由于对Latex不熟，编这两个公式就摸索了一段时间，所以后面的公式就直接截图了。有时间最好还是要学学Latex。

指数映射和对数映射的转换关系

根据上图，就能清晰地看出李群与李代数间的转换关系。

对于指数映射和对射映射的推导，BCH公式近似，李代数求导和扰动模型等内容，就不在此赘述，直接看《视觉SLAM十四讲》就好。

实践

一个较好的李代数库是Strasdat 维护的Sophus 库，安装方法：

git clone https://github.com/strasdat/Sophus.git
cd Sophus
git checkout a621ff
mkdir build
cmake ..
make

演示Sophus 库中的$SO(3)$和$SE(3)$运算：

#include 
#include 
using namespace std; 

#include 
#include 

#include "sophus/so3.h"
#include "sophus/se3.h"

int main( int argc, char** argv )
{
    // 沿Z轴转90度的旋转矩阵
    Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();
    
    Sophus::SO3 SO3_R(R);               // Sophus::SO(3)可以直接从旋转矩阵构造
    Sophus::SO3 SO3_v( 0, 0, M_PI/2 );  // 亦可从旋转向量构造
    Eigen::Quaterniond q(R);            // 或者四元数
    Sophus::SO3 SO3_q( q );
    // 上述表达方式都是等价的
    // 输出SO(3)时，以so(3)形式输出
    cout<<"SO(3) from matrix: "<<SO3_R<<endl;
    cout<<"SO(3) from vector: "<<SO3_v<<endl;
    cout<<"SO(3) from quaternion :"<<SO3_q<<endl;
    
    // 使用对数映射获得它的李代数
    Eigen::Vector3d so3 = SO3_R.log();
    cout<<"so3 = "<<so3.transpose()<<endl;
    // hat 为向量到反对称矩阵
    cout<<"so3 hat=\n"<<Sophus::SO3::hat(so3)<<endl;
    // 相对的，vee为反对称到向量
    cout<<"so3 hat vee= "<<Sophus::SO3::vee( Sophus::SO3::hat(so3) ).transpose()<<endl; // transpose纯粹是为了输出美观一些
    
    // 增量扰动模型的更新
    Eigen::Vector3d update_so3(1e-4, 0, 0); //假设更新量为这么多
    Sophus::SO3 SO3_updated = Sophus::SO3::exp(update_so3)*SO3_R;
    cout<<"SO3 updated = "<<SO3_updated<<endl;
    
    /********************萌萌的分割线*****************************/
    cout<<"************我是分割线*************"<<endl;
    // 对SE(3)操作大同小异
    Eigen::Vector3d t(1,0,0);           // 沿X轴平移1
    Sophus::SE3 SE3_Rt(R, t);           // 从R,t构造SE(3)
    Sophus::SE3 SE3_qt(q,t);            // 从q,t构造SE(3)
    cout<<"SE3 from R,t= "<<endl<<SE3_Rt<<endl;
    cout<<"SE3 from q,t= "<<endl<<SE3_qt<<endl;
    // 李代数se(3) 是一个六维向量，方便起见先typedef一下
    typedef Eigen::Matrix<double,6,1> Vector6d;
    Vector6d se3 = SE3_Rt.log();
    cout<<"se3 = "<<se3.transpose()<<endl;
    // 观察输出，会发现在Sophus中，se(3)的平移在前，旋转在后.
    // 同样的，有hat和vee两个算符
    cout<<"se3 hat = "<<endl<<Sophus::SE3::hat(se3)<<endl;
    cout<<"se3 hat vee = "<<Sophus::SE3::vee( Sophus::SE3::hat(se3) ).transpose()<<endl;
    
    // 最后，演示一下更新
    Vector6d update_se3; //更新量
    update_se3.setZero();
    update_se3(0,0) = 1e-4d;
    Sophus::SE3 SE3_updated = Sophus::SE3::exp(update_se3)*SE3_Rt;
    cout<<"SE3 updated = "<<endl<<SE3_updated.matrix()<<endl;
    
    return 0;
}

该演示程序为分两部分。前半部分介绍SO(3) 上的操作，后半部分则为SE(3)。演示了如何构造$SO(3)$和$SE(3)$对象，对它们进行指数、对数映射，以及当知道更新量后，如何对李群元素进行更新。

为了编译它，请在CMakeLists.txt里添加以下几行：

cmake_minimum_required( VERSION 2.8 )
project( useSophus )

# 为使用 sophus，您需要使用find_package命令找到它
find_package( Sophus REQUIRED )
include_directories( ${Sophus_INCLUDE_DIRS} )

add_executable( useSophus useSophus.cpp )
target_link_libraries( useSophus ${Sophus_LIBRARIES} )

注意：我这里为了方便，直接copy的高博Github上的代码，对于初学者，强烈建议自己手敲一遍代码，并完整的操作一下，不能眼高手低，有些坑是必须要踩的，踩的多了也就成所谓的大佬了。即：无他，唯手熟尔。

总结

李群与李代数，前前后后，学了很多次，每次都有不同的理解。

犹记得第一次接触时，看不动，看不懂。

看的多了，每次重复都能加深理解，关键是不看也不用就忘了，所以在此水一篇，求大佬们轻拍。