视觉SLAM——边缘检测 线段检测 Harris角点检测

前言

本博客为主要学习《计算机视觉——算法与应用》第4章 特征检测与匹配，《OpenCV计算机视觉编程攻略》以及相关知识点的总结与整理。这部分在视觉SLAM十四讲并没有提到，但是很多特征点选取的基础，同时在SLAM算法中也可能会有应用。
主要内容包括：
1、边缘检测算法，常用边缘检测算子
2、直线检测，Hough变换
3、Harris角点检测

边缘检测

边缘定义为亮度剧烈变化的位置。将一幅图像想象为一个高度域，在这样的表面，边缘出现在陡峭斜率上。从数学角度定义一个表面的斜率和方向是通过其梯度实现的：
$$J(x)=\Delta I(x)=(\frac{\partial I}{\partial x},\frac{\partial I}{\partial y})(x)$$

求图像的导数强调了高频部分因而放大了噪声，因此在计算梯度前需要使用低通滤波器进行平滑基础，其中高斯函数是唯一可分离的圆对称滤波器。同时，平滑图像和计算图像梯度是可以合并的：不采取对平滑化的结果求导，而是先对内核求导数，然后与图像卷积：
$$J_{\sigma }(x)=\Delta [G_{\sigma }(x)\ast I(x)]=[\Delta G_{\sigma }(x)]\ast I(x)$$

常用的边缘检测算子

1）Roberts：
交叉微分算子（i+1/2,j+1/2）：边缘定位较准，对噪声敏感。适用于边缘明显且噪声较少的图像分割，会在图像边缘附近的区域内产生较宽的响应，因此边缘定位不是很准确。

2）Sobel：
引入了类似局部平均的运算，因此对噪声具有平滑作用，对灰度渐变和噪声较多的图像处理效果较好，但是对边缘定位比较准确，当精度要求不是很高时是一种常用的方法。

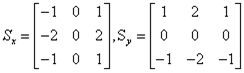
3）Prewitt
对噪声相对不敏感，有抑制噪声作用。但是像素平均相当于对图像的低通滤波，所以对边缘的定位不如Roberts算子。

4）Kirsch：
对灰度渐变和噪声较多的图像处理效果较好。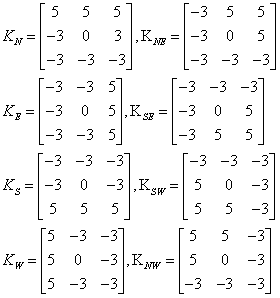

5）Canny：
通常基于Sobel算子，使用两种不同的阈值分别检测强边缘和弱边缘，在低阈值边缘分布图上只保留有连续路径的边缘点，然后把这些边缘点连接到属于高阈值分布图的边缘上。不易受噪声干扰，能够检测到真正的弱边缘。

6）Laplacian：
一种二阶导数算子，对图像中的阶跃性边缘点定位准确，对噪声比较敏感，常用来判断边缘像素视为与图像的明区还是暗区。在边缘处产生一个陡峭的零交叉，是各向同性的，能对任何走向的界线和线条进行锐化。

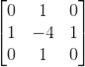
直线检测

这里主要介绍基于Hough变换的直线检测方法，此外还存在基于逐次近似拟合、基于RANSAC的直线检测方法等。

霍夫线变换

直线可以使用Hesse法线式进行表示：$$r=xcos\theta +ysin\theta$$

其中r是原点到直线上最近点的距离，θ是x轴与连接原点和最近点直线之间的夹角，如图1所示。

这个表达式可以将图像中每一条直线与一对参数(r,θ)相关联，这个参数平面被称为霍夫空间。经过霍夫变换，将图像空间中的一个点映射到霍夫空间中，将得到一条正弦曲线。那么多个点形成的直线将产生在(r,θ)处交叉的一组正弦曲线。

具体实现：通过将霍夫参数空间量化为有限间隔的累加器来实现。随着算法的运行，每个算法都把$(x_i,y_i)$转换为一个离散化的$(r,\theta )$曲线，并且沿着这条曲线的累加器单元被递增。当图像空间中所有的像素都经过霍夫变换后，对累加器阵列进行检查，计数值最大的网格（或超过阈值的网格），其坐标值（ρ0, θ0）就对应图像空间中所求的直线。

霍夫变换的优点：
使用基于投票的方法，抗干扰能力强。对图像中直线的殘缺部分、噪声等不敏感。

霍夫变换的缺点：
1）时间复杂度和空间复杂度都很高，当霍夫空间由2维拓展到3维空间或者更高的维度时，计算复杂度几何增长。
2）霍夫参数空间离散化的颗粒度（分辨率）与累加器的阈值（最小投票数）选取困难。
3）在检测过程中只能确定直线方向，丢失了线段的长度信息。

概率霍夫变换对基本算法做了一些修正：首先概率霍夫变换在二值分布图上随机选择像素点，而不是逐行扫描图像。一旦累加器某个入口达到预设最小值，就沿着直线扫描图像，并移除这条直线上的所有像素点，这个扫描过程还可以检测接受的线段长度。

霍夫圆变换

圆的参数方程为$(x-a{)}^2+(y-b{)}^2=r^2$，该方程包含三个参数，传统霍夫变换需要使用三维累加器。

其中OpenCV中采用了霍夫梯度法：先是使用二维累加器找圆心位置，再确定半径。
检测圆心的原理是圆心是其所在圆周所有法线的交点，对每个像素点来说，累加器只对沿着梯度方向的入口增加计数，（根据预先定义的最大和最小半径）；一旦检测到圆心，建立半径值范围的一维直方图，这个直方图的尖峰值就是被检测圆的半径。

角点检测

角点，即拥有至少两个不同方向梯度的图像块，适合作为特征在其他图像中被匹配与跟踪。如果将一个局部的小窗口在各个方向上进行移动，窗口中区域的灰度发生较大变化，则认为是角点。
可以使用加权差的平方和来比较一个图像块与其移动后$(\Delta x,\Delta y)$的变化，即自相关函数：
$$c(x,y,\Delta x,\Delta y)=\sum _{(u,v)\in W(x,y)}w(u,v)(I(u,v)-I(u+\Delta x,v+\Delta y){)}^2$$

其中，$W(x,y)$是以点(x,y)为中心的窗口，$w(u,v)$是高斯加权函数。根据泰勒展开有：

$$I(u+\Delta x,v+\Delta y)=I(u,v)+I_x(u,v)\Delta x+I_y(u,v)\Delta y+O(\Delta x^2,\Delta y^2)$$

其中$I_x,I_y$为图像$I(x,y)$的偏导数，自相关函数可简化为：

$$c(x,y,\Delta x,\Delta y)=\sum _{w}w(u,v)(I_x(u,v)\Delta x+I_y(u,v)\Delta y{)}^2=[\Delta x,\Delta y]M(x,y)\left[\begin{array}{c}\Delta x\\ \Delta y\end{array}\right]$$

其中

$$M(x,y)=\sum _{w}w(u,v)\left[\begin{array}{cc}{I}_x(x,y{)}^2& I_x(x,y)I_y(x,y)\\ I_x(x,y)I_y(x,y)& I_y(x,y{)}^2\end{array}\right]=w\ast \left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]$$

可以使用加权核w进行离散卷积来替换其中的加权求和。这里可以看到图像$I(x,y)$在点(x,y)的自相关函数可以近似为二次项函数：

$$c(x,y,\Delta x,\Delta y)\approx A\Delta x^2+2C\Delta x\Delta y+B\Delta y^2$$

其中
$$A=w\ast I_x^2，B=w\ast I_x{I}_y，C=w\ast I_y^2$$

对$M(x,y)$进行特征值分析，可以产生两个特征值$({\lambda }_1,{\lambda }_2)$及对应的特征向量，其中较大的不确定度取决于较小的特征值，因此通过寻找较小特征值的最大值可以用于寻找特征。

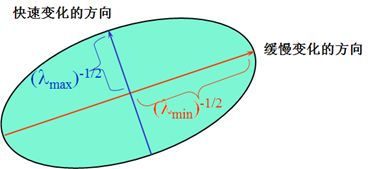
对于不确定性椭圆与图像中的角点、直线与平面有以下三种情况：
1）直线：一个特征值大，一个特征值小，说明自相关函数值在某一方向大，其他方向小；
2）平面：两个特征值都小，且近似相对，说明自相关函数在各个方向都小；
3）角点：两个特征值都大，且近似相等，说明自相关函数在所有方向都大。

其中Harris给出的角点检测方法不需要具体计算特征值，而是计算一个角点相应值R来判断角点：

$$R=det(M)-\alpha trace(M{)}^2={\lambda }_1\ast {\lambda }_2-\alpha ({\lambda }_1+{\lambda }_2{)}^2$$

其中

$$det(M)={\lambda }_1\ast {\lambda }_2=AC-B^2，trace(M)={\lambda }_1+{\lambda }_2=A+C，\alpha 一般可取0.05$$

最后需在3×3或5×5的邻域内进行非最大值抑制，局部最大值点即为图像中的角点。

Harris角点的特点：对亮度和对比度变化不敏感，具有旋转不变性，不具有尺度不变性。