The Elements of Statistical Learning的笔记

• 1. The Problem of Overfitting

  

  1

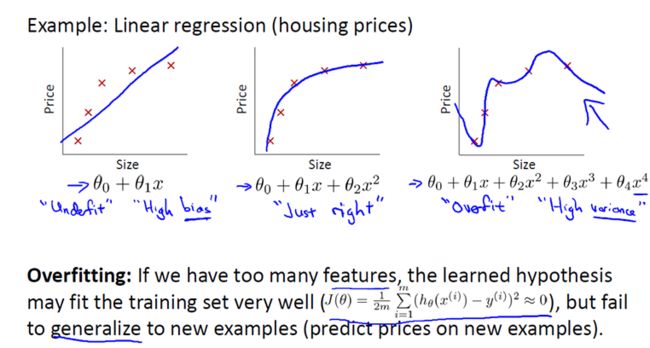
  还是来看预测房价的这个例子，我们先对该数据做线性回归，也就是左边第一张图。

  如果这么做，我们可以获得拟合数据的这样一条直线，但是，实际上这并不是一个很好的模型。我们看看这些数据，很明显，随着房子面积增大，住房价格的变化趋于稳定或者说越往右越平缓。因此线性回归并没有很好拟合训练数据。

  我们把此类情况称为欠拟合(underfitting)，或者叫作叫做高偏差(bias)。

  这两种说法大致相似，都表示没有很好地拟合训练数据。高偏差这个词是 machine learning 的研究初期传下来的一个专业名词，具体到这个问题，意思就是说如果用线性回归这个算法去拟合训练数据，那么该算法实际上会产生一个非常大的偏差或者说存在一个很强的偏见。

  第二幅图，我们在中间加入一个二次项，也就是说对于这幅数据我们用二次函数去拟合。自然，可以拟合出一条曲线，事实也证明这个拟合效果很好。

  另一个极端情况是，如果在第三幅图中对于该数据集用一个四次多项式来拟合。因此在这里我们有五个参数θ₀到θ_4，这样我们同样可以拟合一条曲线，通过我们的五个训练样本，我们可以得到如右图的一条曲线。

  一方面，我们似乎对训练数据做了一个很好的拟合，因为这条曲线通过了所有的训练实例。但是，这实际上是一条很扭曲的曲线，它不停上下波动。因此，事实上我们并不认为它是一个预测房价的好模型。

  所以，我们把这类情况叫做过拟合(overfitting)，也叫高方差(variance)。

  与高偏差一样，高方差同样也是一个历史上的叫法。从第一印象上来说，如果我们拟合一个高阶多项式，那么这个函数能很好的拟合训练集（能拟合几乎所有的训练数据），但这也就面临函数可能太过庞大的问题，变量太多。

  同时如果我们没有足够的数据集（训练集）去约束这个变量过多的模型，那么就会发生过拟合。

  2

  过度拟合的问题通常发生在变量（特征）过多的时候。这种情况下训练出的方程总是能很好的拟合训练数据，也就是说，我们的代价函数可能非常接近于 0 或者就为 0。

  但是，这样的曲线千方百计的去拟合训练数据，这样会导致它无法泛化到新的数据样本中，以至于无法预测新样本价格。在这里，术语"泛化"指的是一个假设模型能够应用到新样本的能力。新样本数据是指没有出现在训练集中的数据。

  
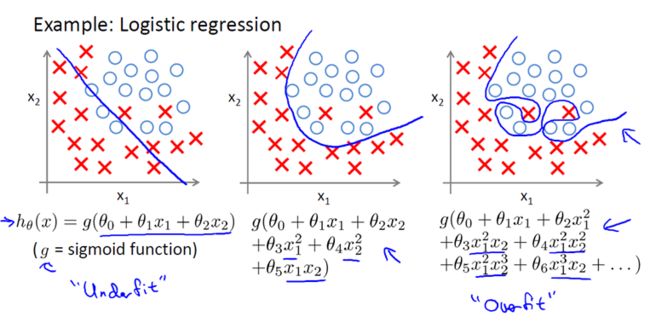
  之前，我们看到了线性回归情况下的过拟合。类似的情况也适用于逻辑回归。

  3

  那么，如果发生了过拟合问题，我们应该如何处理？

  过多的变量（特征），同时只有非常少的训练数据，会导致出现过度拟合的问题。因此为了解决过度拟合，有以下两个办法。

  

  方法一：尽量减少选取变量的数量
  

  具体而言，我们可以人工检查每一项变量，并以此来确定哪些变量更为重要，然后，保留那些更为重要的特征变量。至于，哪些变量应该舍弃，我们以后在讨论，这会涉及到模型选择算法，这种算法是可以自动选择采用哪些特征变量，自动舍弃不需要的变量。这类做法非常有效，但是其缺点是当你舍弃一部分特征变量时，你也舍弃了问题中的一些信息。例如，也许所有的特征变量对于预测房价都是有用的，我们实际上并不想舍弃一些信息或者说舍弃这些特征变量。

  方法二：正则化

  正则化中我们将保留所有的特征变量，但是会减小特征变量的数量级（参数数值的大小θ(j)）。

  这个方法非常有效，当我们有很多特征变量时，其中每一个变量都能对预测产生一点影响。正如我们在房价预测的例子中看到的那样，我们可以有很多特征变量，其中每一个变量都是有用的，因此我们不希望把它们删掉，这就导致了正则化概念的发生。

  接下来我们会讨论怎样应用正则化和什么叫做正则化均值，然后将开始讨论怎样使用正则化来使学习算法正常工作，并避免过拟合。

  2. Cost Function

  

  1

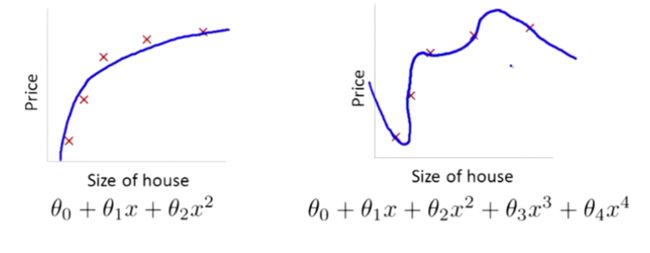
  在前面的介绍中，我们看到了如果用一个二次函数来拟合这些数据，那么它给了我们一个对数据很好的拟合。然而，如果我们用一个更高次的多项式去拟合，最终我们可能会得到一个曲线，它能很好地拟合训练集，但却并不是一个好的结果，因为它过度拟合了数据，因此，一般性并不是很好。

  让我们考虑下面的假设，我们想要加上惩罚项，从而使参数 θ₃ 和 θ₄ 足够的小。

  

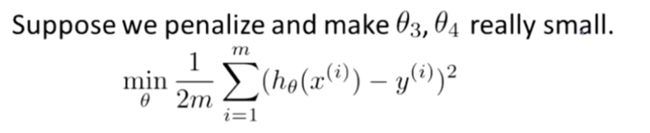
  这里我的意思就是，上图的式子是我们的优化目标，也就是说我们需要尽量减少代价函数的均方误差。

  对于这个函数我们对它添加一些项，加上 1000 乘以 θ₃ 的平方，再加上 1000 乘以 θ₄ 的平方，

  

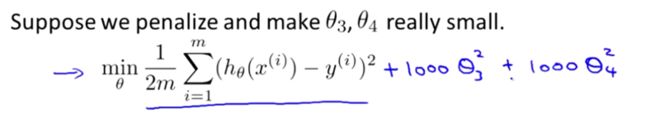
  1000 只是我随便写的某个较大的数字而已。现在，如果我们要最小化这个函数，那么为了最小化这个新的代价函数，我们要让 θ₃ 和 θ₄ 尽可能小。因为，如果你在原有代价函数的基础上加上 1000 乘以 θ₃ 这一项 ，那么这个新的代价函数将变得很大，所以，当我们最小化这个新的代价函数时， 我们将使 θ₃ 的值接近于 0，同样 θ₄ 的值也接近于 0，就像我们忽略了这两个值一样。如果我们做到这一点（ θ₃ 和 θ₄ 接近 0 ），那么我们将得到一个近似的二次函数。

  

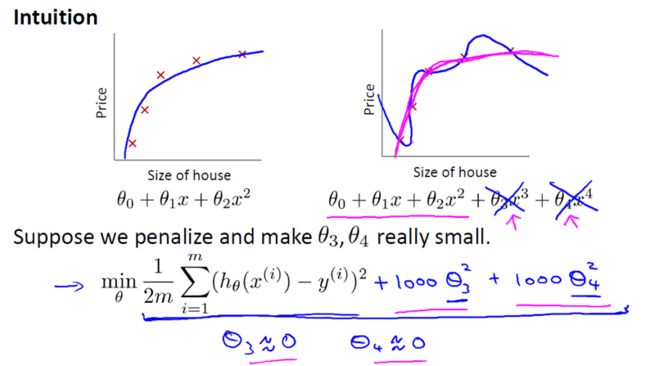
  因此，我们最终恰当地拟合了数据，我们所使用的正是二次函数加上一些非常小，贡献很小项（因为这些项的 θ₃、 θ₄ 非常接近于0）。显然，这是一个更好的假设。

  2

  

  更一般地，这里给出了正规化背后的思路。这种思路就是，如果我们的参数值对应一个较小值的话（参数值比较小），那么往往我们会得到一个形式更简单的假设。

  在我们上面的例子中，我们惩罚的只是 θ₃ 和 θ_{4 ，}使这两个值均接近于零，从而我们得到了一个更简单的假设，实际上这个假设大抵上是一个二次函数。

  但更一般地说，如果我们像惩罚 θ₃ 和 θ₄ 这样惩罚其它参数，那么我们往往可以得到一个相对较为简单的假设。

  实际上，这些参数的值越小，通常对应于越光滑的函数，也就是更加简单的函数。因此 就不易发生过拟合的问题。
  

  我知道，为什么越小的参数对应于一个相对较为简单的假设，对你来说现在不一定完全理解，但是在上面的例子中使 θ₃ 和 θ₄ 很小，并且这样做能给我们一个更加简单的假设，这个例子至少给了我们一些直观感受。

  来让我们看看具体的例子，对于房屋价格预测我们可能有上百种特征，与刚刚所讲的多项式例子不同，我们并不知道 θ₃ 和 θ₄ 是高阶多项式的项。所以，如果我们有一百个特征，我们并不知道如何选择关联度更好的参数，如何缩小参数的数目等等。

  因此在正则化里，我们要做的事情，就是把减小我们的代价函数（例子中是线性回归的代价函数）所有的参数值，因为我们并不知道是哪一个或哪几个要去缩小。

  因此，我们需要修改代价函数，在这后面添加一项，就像我们在方括号里的这项。当我们添加一个额外的正则化项的时候，我们收缩了每个参数。

  

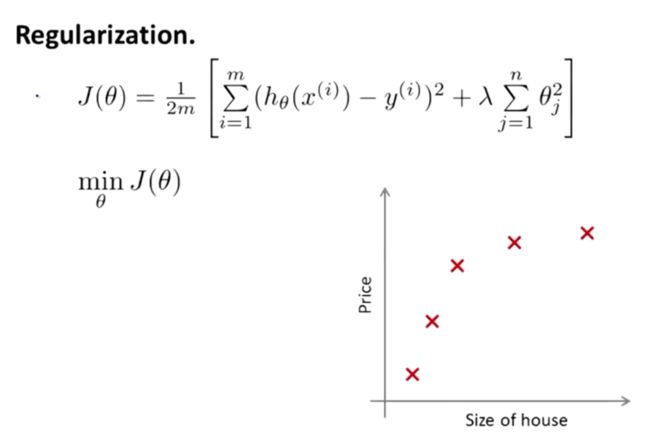
  顺便说一下，按照惯例，我们没有去惩罚 θ₀，因此 θ₀ 的值是大的。这就是一个约定从 1 到 n 的求和，而不是从 0 到 n 的求和。但其实在实践中
  这只会有非常小的差异，无论你是否包括这 θ₀ 这项。但是按照惯例，通常情况下我们还是只从 θ₁ 到 θ_n 进行正则化。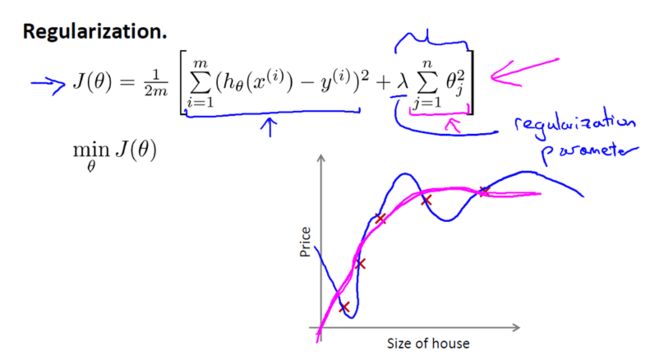

  

  
  下面的这项就是一个正则化项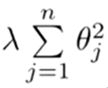

  
  并且 λ 在这里我们称做正则化参数。

  λ 要做的就是控制在两个不同的目标中的平衡关系。
  

  第一个目标就是我们想要训练，使假设更好地拟合训练数据。我们希望假设能够很好的适应训练集。

  而第二个目标是我们想要保持参数值较小。（通过正则化项）

  而 λ 这个正则化参数需要控制的是这两者之间的平衡，即平衡拟合训练的目标和保持参数值较小的目标。从而来保持假设的形式相对简单，来避免过度的拟合。

  对于我们的房屋价格预测来说，我们之前所用的非常高的高阶多项式来拟合，我们将会得到一个非常弯曲和复杂的曲线函数，现在我们只需要使用正则化目标的方法，那么你就可以得到一个更加合适的曲线，但这个曲线不是一个真正的二次函数，而是更加的流畅和简单的一个曲线。这样就得到了对于这个数据更好的假设。

  再一次说明下，这部分内容的确有些难以明白，为什么加上参数的影响可以具有这种效果？但如果你亲自实现了正规化，你将能够看到这种影响的最直观的感受。

  3

  

  在正则化线性回归中，如果正则化参数值 λ 被设定为非常大，那么将会发生什么呢？

  我们将会非常大地惩罚参数θ₁ θ₂ θ₃ θ₄ … 也就是说，我们最终惩罚θ₁ θ₂ θ₃ θ₄ …  在一个非常大的程度，那么我们会使所有这些参数接近于零。

  

  如果我们这么做，那么就是我们的假设中相当于去掉了这些项，并且使我们只是留下了一个简单的假设，这个假设只能表明房屋价格等于 θ₀ 的值，那就是类似于拟合了一条水平直线，对于数据来说这就是一个欠拟合 (underfitting)。这种情况下这一假设它是条失败的直线，对于训练集来说这只是一条平滑直线，它没有任何趋势，它不会去趋向大部分训练样本的任何值。

  这句话的另​​一种方式来表达就是这种假设有过于强烈的"偏见" 或者过高的偏差 (bais)，认为预测的价格只是等于 θ₀ 。对于数据来说这只是一条水平线。

  因此，为了使正则化运作良好，我们应当注意一些方面，应该去选择一个不错的正则化参数 λ 。当我们以后讲到多重选择时我们将讨论一种方法来自动选择正则化参数 λ  ，为了使用正则化，接下来我们将把这些概念应用到到线性回归和逻辑回归中去，那么我们就可以让他们避免过度拟合了。

  3. Regularized Linear Regression

  之前我们已经介绍过，岭回归的代价函数如下：

  
  对于线性回归(的求解)，我们之前运用了两种学习算法，一种基于梯度下降，一种基于正规方程。

  1

  梯度下降，如下：

  

  2

  正规方程，如下：

  

  3

  

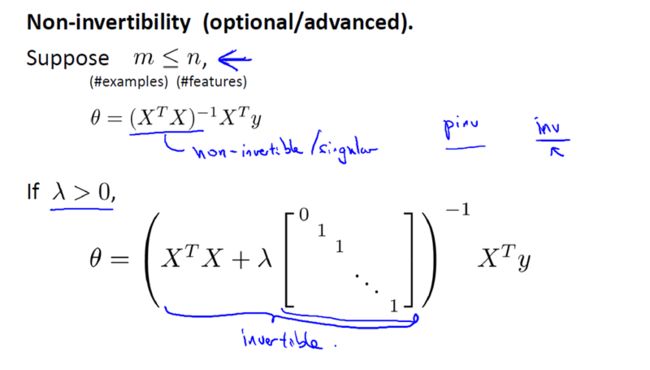
  现在考虑 M（即样本量）， 比 N（即特征的数量）小或等于N。

  通过之前的博文，我们知道如果你只有较少的样本，导致特征数量大于样本数量，那么矩阵 X^TX 将是不可逆矩阵或奇异（singluar）矩阵，或者用另一种说法是这个矩阵是退化（degenerate）的，那么我们就没有办法使用正规方程来求出 θ 。

  幸运的是，正规化也为我们解决了这个问题，具体的说只要正则参数是严格大于零，实际上，可以证明如下矩阵：

  

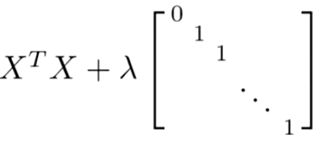
  将是可逆的。因此，使用正则还可以照顾任何 X^TX 不可逆的问题。
  
  所以，你现在知道如何实现岭回归，利用它，你就可以避免过度拟合，即使你在一个相对较小的训练集里有很多特征。这应该可以让你在很多问题上更好的运用线性回归。

  在接下来的视频中，我们将把这种正则化的想法应用到 Logistic 回归，这样我们就可以让 logistic 回归也避免过度拟合，从而表现的更好。

  4. Regularized Logistic Regression

  Regularized Logistic Regression 实际上与 Regularized Linear Regression 是十分相似的。

  

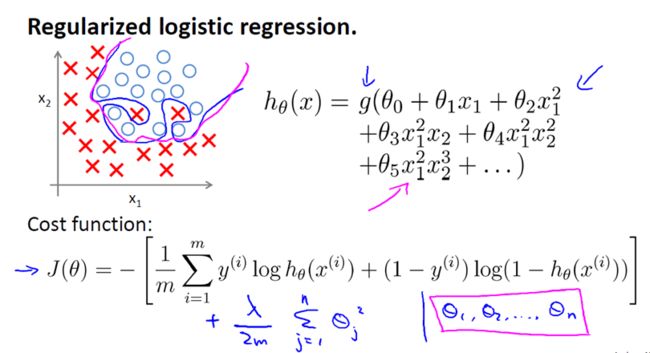
  同样使用梯度下降：

  

  如果在高级优化算法中，使用正则化技术的话，那么对于这类算法我们需要自己定义costFunction。

  For those methods what we needed to do was to define the function that's called the cost function.

  

  这个我们自定义的 costFunction 的输入为向量 θ ，返回值有两项，分别是代价函数 jVal 以及 梯度gradient。

  总之我们需要的就是这个自定义函数costFunction，针对Octave而言，我们可以将这个函数作为参数传入到 fminunc 系统函数中（fminunc 用来求函数的最小值，将@costFunction作为参数代进去，注意 @costFunction 类似于C语言中的函数指针），fminunc返回的是函数 costFunction 在无约束条件下的最小值，即我们提供的代价函数 jVal 的最小值，当然也会返回向量 θ 的解。

  上述方法显然对正则化逻辑回归是适用的。

  5. 尾声

  通过最近的几篇文章，我们不难发现，无论是线性回归问题还是逻辑回归问题都可以通过构造多项式来解决。但是，你将逐渐发现其实还有更为强大的非线性分类器可以用来解决多项式回归问题。下篇文章中，我们将会讨论。

  
  

• 第二章

  最近在阅读这本elements of statistical learning，这本书的题目翻译成中文可以叫做统计学系基础。但是我认为这本书非常之不基础。需要读者具备比较扎实的数理统计和概率论的功底，对于统计推断，统计决策以及基本的机器学习的概念有所了解。我所阅读的是从学校图书馆借来的影印本，内容为本书第一版（2001）。据说第二版有700多页那么厚。

  这本书有中文翻译版，但是翻译作者可能非统计专业出身，很多专有名词不光翻译不准确，另外很多语句也翻译的很奇怪。因此，建议本书的读者还是阅读影印本或者从作者网站下载原本比较好。
  本书阅读已经进行了将近两周的时间，大致上阅读了前四章的内容。觉得内容虽不艰深，但是也绝不基础。是本非常好的书。决定现在开始，定期写点读书笔记上来，做个小结。
  第二章的题目是有指导学习概述。所谓的有指导学习，在我理解来看，就是真实的输出或者响应事实上是已知的，在这种情况下利用输入数据，构建一定的模型来预测输出，再通过和真实输出值之间进行比较，从而调整模型，减少模型的预测误差。而所谓的统计学习，这个概念和机器学习既有联系又有所不同。统计学系，我认为是机器学习的一个特殊的情况，从数学和统计学的角度看待问题，事实上是在利用统计学的模型做函数逼近。统计学模型的建模，大致上有两种不同的思路，这也是本书第二章第三节所介绍的最小二乘和最近邻方法。在统计学中，最小二乘是参数统计中构建线性模型的求解方法，事实上最小二乘是一种最优化算法。而最近邻方法则是非参数统计建模的基本思想之一。最小二乘的前提是对统计模型做出一定的假定，比如说统计模型是全局线性的(非线性回归模型也有相应的最优化解法)。而最近邻方法则认为距离相近的点，其相应的输出应该差不了太多。后面我们会看到，这种方法的一些局限及其推广。
  2.3节介绍完最小二乘以及最近邻方法之后，2.4节介绍了一些基本的统计决策理论。我认为，并且深刻的认为，统计决策的理论，是整个统计学习的理论基础，因此有必要好好梳理一下统计决策理论的思路。
  统计决策理论，我记得是在大三的时候学的。现在留下的最深的印象其实就是贝叶斯公式的各种推倒。事实上，所谓的决策，是需要将决策问题的分析化为两部分，第一部分是寻找损失函数，也就是通过分析，得出你所做的决策可能发生的损失。在统计学中，损失函数有很多种，而损失函数归根到底，也就是在某种分布下的期望。决策的第二步就是从损失函数出发，求解使得损失最小的参数设置，这个参数设置就是我们的决策。那么从统计学习的角度来讲，有输入X，也有输出Y，这两者之间的联合分布P(X,Y)是我们知道的。如果我们选用最常用的平方和损失，那么可以得到在联合分布P(X,Y)下平方和损失的期望。我们将这个期望当成是我们选择模型的准则。使得这个值最小的模型即使我们所选择的模型。那么建模问题就变成了统计决策的问题。利用条件期望与期望之间的关系，我们得到，在损失平方和的期望的准则之下，最优的解是关于X的Y的条件期望。这个解是我们所熟识的，在线性模型中，我们也证明过条件期望是使得该准则达到最小的唯一的解。
  到现在，我们应该注意到，所建构的模型是一个条件期望。而如果要确切知道条件期望，我们必须知道条件概率分布或者条件密度。而事实上，如果我们知道了这些，我们其实也就没有必要来建模了。我们所知道的仅仅是数据，我们需要利用数据来估计这个条件概率分布或者条件密度。举一个例子，在有指导学习的分类问题中，我们就可以利用不同类别所占的比例来估计这个类别的概率分布，用在该类别下的输入的数据来估计输入变量的先验概率分布，然后用贝叶斯公式就可以求得后验概率分布了。
  事实上，最小二乘与最近邻都是对这个条件期望的估计。我们先拿最近邻说事儿。事实上，我认为最近邻相比最小二乘，是一个更加“统计”的东西，最小二乘更像是一个数学的最优化问题。最近邻方法，是用某个目标值点附近的几个点对应的输出的平均值最为该目标输入点对应的输出的估计（预测）。事实上，也是一个条件均值，条件就是求均值的这几个值必须是目标点的某个近邻中的点所对应的输出。这里有两次近似，一次是用平均值来近似均值，另外，就是某个点上的条件分布，我们用这个点的近邻来近似。可以证明，当训练样本数量足够大的时候，最近邻方法是收敛到上述所需要的条件期望的。这是一个非常好的大样本性质。这个至少说明了最近邻方法是从理论上来讲是非常合理的。稍后我们会看到在实际应用中，这种方法的局限。
  讲完了最近邻方法是如何纳入到统计决策的问题框架下的，下面我们来看一看线性回归是如何纳入到这个框架下来的。线性回归，事实上只是参数回归问题的一种，参数回归中，线性回归的起源最早，原因是其模型假设最简单。其假设模型参数是线性的。在这个前提假设之下进行模型的搜索。事实上，我们不应该忘记我们始终要寻找的，其实是条件期望。正因为没有确切知道条件概率分布我们才用其他方法找寻条件期望的一个估计。我们把线性假设放在条件期望中，这样做事实上缩小了搜索最优解的范围，而且在这个限制之下，我们也是可以求得理论解的。我们通常所使用的最小二乘解其实也仅仅是这个理论解的一种估计。
  此外，我们可以更换损失函数，比如L1范数的损失函数，得到的理论的最优解是条件中位数，那么这个也可以用样本中位数去估计。当输出是定性变量的时候，我们也可以通过编码，以及改变损失函数的结构，来将分类问题纳入到统计决策的理论框架中来。而这就是所谓的贝叶斯分类器。我想对此感兴趣的读者应该去看看原文，那里的推导是令人感到赏心悦目的。
  本章2.5节接着介绍了局部方法在高维情况下所遇到的很多问题。虽然局部方法的大样本性质很好，但是高维情况下，出现了很多不适合用局部方法求解的问题。这里我就不一一介绍了。我认为这部分内容只要知其然就可以了，本章课后有一道习题，是要推导高维球体离球心最近点的分布情况的，看了就傻眼。
  介绍完高维灾难之后，本书2.6节理清了统计模型，有指导学习以及函数逼近三者之间的逻辑联系，相同点和不同点。值得一提的是，在函数逼近部分，作者终于提出了极大似然方法，这个在统计中，我认为最重要的方法。
  在2.7节，作者提到了一些结构化的回归方法，事实上这个方法可以看成是线性模型的相应推广，目的是为了解决高维情况下局部方法的不足。2.8节，也是综述性的介绍了统计模型的分类，我觉得这部分的内容还是比较有趣的。也有必要梳理一下。下面开始简单的梳理。
  统计模型，从本源来看，一种是从最近邻方法发展出来的局部方法，另外一种则是对线性模型的相应的改进。当然，这样的划分或许并不是那么准确，因为有些模型则是二者之间的混搭。
  第一种，加惩罚项的回归。目前用的比较火的有很多变量选择的方法，比如lasso，岭回归，桥回归。是研究的一个热点，其本质是对损失加惩罚，从而达到对系数的压缩。
  第二种，核方法，这个是非参数回归中的一种非常重要的方法，引入核函数，对点与目标点之间的关系附上权重，相当于是将最近邻方法中的求均值变成了求加权平均值。是最近邻方法的推广。
  第三种，基函数方法。这个是对线性模型的推广，假设模型仍然是可加的，对系数而言仍然是线性的，但是所加的这些项则变成了函数（基函数），对这种方法而言，比较常用的一个是样条，另外一个是多项式回归。在地理统计学和计算机试验的建模中，也有一个所谓的kriging方法，也可以划分为这个类别。
  以上的分类，对于我们学习统计建模或者说统计学习，是很有帮助的。我们知道了某种方法的来源，就可以对这种方法进行改进。就比如说Efron提出的最小角回归方法，正是看清了逐步回归的本质，才做了相对的改动提出来的。就我个人的经验而言，所有统计学上的进步，至少我所阅读过的四大顶级杂志中的文章，其都是看明白了某种统计方法的本质，然后在此基础上做了相应的改进的。
  本章的最后一节，谈了模型选择的问题，事实上，模型选择所涉及的问题是一个平衡模型复杂程度以及预测精度的问题。所提出的模型选择准则，无非是对上述问题的从某种角度来说比较合理的解答。对于模型选择，我更愿意关注的一些策略，比如cross-validation，boosting等等。
  以上就是我对第二章的阅读的一些心得。第二章仅仅是本书的开局，所介绍的内容都是非常基本的，也是很概括的。后续章节逐步深入展开，难度也增加不少。继续加油阅读吧。
  2012-10-30 11:16:26  15回应

• 分类的线性方法

  这两天看这本书，每天都要遭受不同程度的打击。读起来进度非常之慢，并且时不时会卡壳。如果有童鞋能够一块讨论，一定会受益匪浅。下面小结一下这几天看书的一些心得吧。

  本书的第三章内容是线性回归，包括了很多变量选择的内容。这部分内容，我暂时先不写笔记。在我们已经拥有了线性回归的相关的基本知识之后，我们来看第四章。第四章的题目是linear methods for classification。众所周知，分类是机器学习，数据挖掘的最重要的任务之一。而线性方法则是这些方法中最为基本的，往往也是比较有效地，因此需要花费精力来学习这些基本的内容。
  首先，所谓的分类问题，是一种有指导的学习，也就是说我们知道数据本身属于哪一类，我们要做的是找出数据分类的规则，以便对于新的数据进行分类。第二，我们要搞清楚什么是线性方法，线性到底意味着什么。我们举一个非常直观的例子。
  上面的图中所表示的是一个线性判别分析分类的结果。数据是二维的，分成三类，分别用不同颜色的点表示。图中的黑色的直线，则是线性判别函数所得到的分类的边界。我们可以看到，分类的边界关于二维输入变量是线性的。（在二维情况下，直观看来就是直线）。推广到高维的情况，分类边界如果是超平面或者仿射集（affine set，这个东西我到现在也没搞懂是什么，但是没关系，我们就知道是超平面就行，不影响理解），那么就可以说这个分类的方法是线性的。更进一步的，如果分类的边界可以表示成输入变量的线性组合，我们就说是用线性方法进行分类的。我们不妨称这样的分类的准则为线性分类器。
  事实上，线性方法有很多种。我们最常见的就是传说的线性回归模型，此外，还有logistic回归，线性判别分析，以及分隔平面法。我们下面一一介绍。
  （1）线性回归模型。
  要用线性回归的方法来学习分类的规则，重要的一步是对输出进行编码（code）。编码的目的是使得定性的输出变量能够定量化，然后套用线性回归，最小二乘之类的即可。编码的想法也很简单，比如说我们的输出集合一共有K个类，那么我们就产生K个指标变量($Y_k$)，($k=1,\ldots,K$)，如果输出确实属于第k类，则($Y_k=1$)，其他的($Y_l=0$)。这样对于每行观测，我们都有K个指标来表示其输出。这就把问题转化为了多元回归的问题。而且在这里，回归问题更加简单，若训练样本有N行观测，则会有一个($N \times K$)的指标矩阵($\textbf{Y}$)，这个矩阵每一行只有一个1，剩下的都是0.对于这个矩阵的每一列，我们同时用最小二乘进行回归就得到了一个拟合的模型 ($\hat{\textbf{Y}}=\textbf{X}(\textbf{X}^T\textbf{X})^{-1}\textbf{X}^T\textbf{Y}$) 对于一个新的观测，我们如何通过上式进行判断呢？
  我们首先将新的观测代入拟合的模型，从而得到了一个输出。这个输出肯定是一个K维的向量。然后我们找出这个向量元素中最大的值，比如第m个元素最大，我们就把这个观测分类为第m类。
  这就是线性回归分类器（我们姑且这么称呼他，我才疏学浅，并不知道是否有此方法的确切称呼）。我们可以继续探究一下用这种方法进行分类的道理。它的合理性在哪。我们知道，线性回归模型得出的结果是对条件期望的估计，而对于如上编码的情况，条件期望正是分类的后验概率分布。这一点，强有力的支持了我们用线性回归做分类问题。
  除此以外，我们还有另外一种利用线性回归方法解决分类问题的视角，视角不同，但是结果与上述内容完全相同。
  线性回归方法简单，但是简单也有简单的问题。对于三个类别以上的分类问题，尤其是当类别数比较大的时候，由于线性回归对模型的要求过于严格，因此分类肯定会有重叠。下图是原书中的一个例子
  我们看到，中间蓝色的类完全被忽略了。也就是说蓝色的这一类分类全部是错误的。
  这个肯定是我们不想看到的。因此，我们需要想一些方法来解决。解决的方法，其思想核心与我们试验设计中考察交互作用，对交互项进行回归的思想很像。也就是说我们考虑变量之间的交互效应，拟合多项式回归模型，当多项式回归模型阶数合适的时候，可以减轻上述问题带来的困扰。这个就不多展开讲了。（这一部分是我的主修课程试验设计数据分析中的一个很重要的部分，实在是不想展开多讲）。
  （2）线性判别分析
  关于判别分析，最早是在多元统计分析这门课中学习的。当时年轻不懂事儿，多元统计分析没认真学习，课后作业也都是抄同学的。而且这些年，几乎没有什么实际的例子用判别分析，因此，对于这部分内容基本上脑袋里一片空白。还好这本书对于判别分析的介绍相对来说还是比较容易理解的。
  统计决策理论告诉我们，如果我们要做一个最优的分类，我们需要知道分类的后验概率分布情况。仍然假设有K个类别，($\pi_k$)是这K个类别的先验概率，显然($\sum_{i=1}^K \pi_k=1$)，并且我们知道每一个类别内部的数据的分布情况($f_k(x)$)。我们利用贝叶斯公式就可以求得分类的后验概率分布 ($p(G=k|X=x)=\frac{f_k(x)\pi_k}{\sum_{l=1}^K f_l(x)\pi_l}$)
  _______________________
  而线性判别分析，则是假设类别内部数据是服从正态分布的。当然还有其他分布的假设，本书后续的内容也会涉及到。）
  下面我们来看一看什么是线性判别分析。
  我们假设每一个类内部的数据密度是多元正态的，并且协方差矩阵相同。即如下： ($f_k(x)=\frac{1}{(2\pi)^{\frac{p}{2}}\|\Sigma\|^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k)\}$)
  并且我们可以简单的推到，看到两个类别的后验概率之比再取对数得到的结果关于输入($x$)是线性的。也就是说分类边界对输入($X$)是线性的。因此这个分类器叫做线性判别分析。
  以上就是线性判别分析的基本的想法。而从这个想法中再提炼，我们得到所谓的线性判别函数： ($\delta=x^T\Sigma^{-1}\mu_k-\frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k+log\pi_k$) 分类的规则也是对于一个新的输入($x$)，我们找到是的($\delta_k(x)$)最大的k，然后就把($x$)归类为类别k。
  对于上述判别函数，有三个参数需要利用训练样本进行估计，先验分布，正态分布的均值以及协方差阵。这些都可以利用最简单的点估计来估计。这里也不多提了。
  本书的后续部分介绍了一点二次判别分析的内容，这部分内容在我的笔记里也不体现了。回头有时间，会把这些内容做一个整合，写点笔记。
  对于线性判别分析，当类别比较多的时候，降秩成为了一个有趣的话题。降秩问题源于当类别比较多的时候，理论上证明了一个原空间的低维子空间可以很好的代表原空间，并且在分类问题上没有任何的信息损失。这就涉及到如何找到这个低维的子空间。Fisher运用特征分解的方法，很好的解决了这个问题。关于这个问题，原书的内容讲的很清楚，此外，宾夕法尼亚州立大学统计系的网页上有一个相关问题的课件，对此问题也讲的很清晰。关于这个问题我昨天看了整整一个上午，大致的推导过程不会太难。
  在R里，MASS包中的lda()函数可以做线性判别分析。
  上面的图片是原书里的一个模拟的例子，我们可以看到线性判别分析的分类效果是挺不错的。
  （3）logistic回归
  logistic回归可以视作是广义线性回归模型的一种。陈希孺先生在国内的某个杂志上有连载10篇论文，介绍广义线性模型。内容相对来说比较理论，比较艰深。现在广义线性模型的应用比较广泛。在我看来，如果单纯要应用logistic回归做分类问题，我们只要把它看成是线性回归的简单推广即可。具体的学理的部分，有能力者可以去学习下，如要应用起来，或许不一定需要那么多理论的知识。
  首先，我们需要分类的边界是线性的。 ($log\frac{p(G=1|X=x)}{p(G=K|X=x)}=\beta_{10}+\beta_1^Tx$) ($log\frac{p(G=2|X=x)}{p(G=K|X=x)}=\beta_{20}+\beta_2^Tx$) ($\cdots$) ($log\frac{p(G=K-1|X=x)}{p(G=K|X=x)}=\beta_{(K-1)0}+\beta_{K-1}^Tx$) 然后呢，我们需要后验概率加起来肯定是1.因此我们选择logistic变换 ($p(G=k|X=x)=\frac{exp(\beta_{k0}+\beta_k^Tx)}{1+\sum_{l=1}^{K-1}exp(\beta_{l0}+\beta_l^Tx)}$)，($k=1,\ldots,K-1$)
  ($p(G=k|X=x)=\frac{1}{1+\sum_{l=1}^{K-1}exp(\beta_{l0}+\beta_l^Tx)}$)
  显然，这个变换是符合了上述的条件的。
  通常情况下，logistic模型并不是由最小二乘法拟合得到的，而是利用了极大似然方法。关于这个模型的求解，用到了Newton-Raphson算法，到目前为止我还没太搞明白这个最优化算法（下一步应该学点最优化方面的东西了）。总之，这个算法是一个迭代的过程，通过迭代，得到参数的估计，满足目标函数。（btw，从某种角度来讲，所有的参数回归模型，包括线性回归，广义线性回归，非线性回归，都是最优化问题）。
  logistic回归在R中的函数glm。
  到目前为止，我们应该可以发现一个比较有趣的问题，就是线性判别分析和logistic回归的分类边界的模型事实上是一样的。都是x的线性函数。二者的差别在于线性判别分析估计参数的方法是最小二乘，而且对模型的约束很多，包括正态性假设以及等协方差函数的假设，而logistic回归则限制少了很多，参数的估计方法也用了更为一般化的极大似然估计。更为理论的内容书中也有所介绍。感兴趣的读者可以去推导一下那部分的公式，也是挺有意思的。
  下面进入本次读书笔记的最后一部分
  （4）seperating hyperplanes
  这个我不太清楚怎么翻译，翻译成”分隔超平面“？事实上，正是这部分内容令我感到非常的郁闷，看了很久也不是很明白。我们直接看看书上是怎么说的吧。
  书上首先举了一个例子
  这个图中一共有20个点，来自于二维欧式空间，这些点属于两个不同的类，分别用不同的颜色来区分。我们可以看到图中有几条分隔的直线，而事实上，这样的分隔的直线是有无穷多条的。我们的目的，是从这无穷多的超平面中搜索出一个分类效果最好的。用到的算法是Rosenblatt's perceptron learning algorithem,具体的算法，我实在也是没心思看了，每次不管看书还是看文章，看到最后部分都是匆忙略过。妈的。
  总之，如果点没有被分隔开的话，这个算法是不会收敛的。之后的部分属于作者标出来的难点
  所以我直接就没看……
  今儿就到这了。继续努力吧，先至少把这本书从头到尾过一遍。
  2011-11-02 17:15:21  4回应

• 5.2 分段多项式和样条

  本次笔记的内容主要是集中于第五章的第二节。第五章的内容比较重，因此计划每一小节读完都写点笔记，并且尽量给出这些内容在R中的实现。下面开始：

  分段多项式，是通过把输入变量($X$)的取值空间分割成连续的区间，然后在每个区间中进行多项式拟合得到的。分段多项式是基函数回归的一种，因此，我们可以用基函数的模子来描写这个多项式。
  分段拟合多项式会遇到问题，就是在结点处，所拟合的多项式不连续。一般来说，我们比较希望拟合得到的函数是连续的，甚至更光滑的，因此我们要增加一些限制条件。比如要求结点处，两边的多项式值相等。或者更光滑的，一阶，二阶微分也是连续的。
  我们需要注意的一点是，分段多项式的基函数可以有不同的表达，通常truncated power basis是一个简单的表达，但是在计算的时候，当结点数太多的时候会有问题。B样条基能够比较有效地解决这个问题，因此在大多数的统计软件中，都是用B样条基来作为分段多项式回归的基函数的。（B样条基在后续的笔记中会介绍到，这里就不叙述了）。
  关于样条和分段多项式，它们之间的联系很紧密。一个有着结点($\xi_j,j=1,\ldots,K$)的M阶样条，是一个M阶的分段多项式，并且该分段多项式的M-2次微分都是连续的。比如说一个三次样条(cubic spline)，阶数($M=4$)。并且，有人指出，三次样条是人眼无法辨别结点处不连续的最低阶的样条。也就是说，三次样条以上的样条，在结点处，看起来都是连续的。在实际中，常用的样条的阶数为1,2,4。
  在用样条进行回归也好，分类也好，我们都必须要选择样条的阶数，样条中结点的个数以及结点的位置。
  下面介绍一个非常常用的样条，自然三次样条（natural cubic spline）。我们知道，多项式模型在变量的边界部分波动很大，用了分段多项式以后，每一个结点出的拟合的波动都比较大，这是一个问题。自然三次样条就是通过多加一些限制，来缓解这个问题。当然，缓解这个问题所付出的代价就是结点部分的拟合的偏差可能会增大。但是，这是一个平衡。这个额外的限制是，在结点两侧的边界部分，限制所拟合的函数是线性的。我们来直接看看有K个结点的自然三次样条的K的基函数是长什么样的： ($N_1(X)=1,N_2(X)=X,N_{k+2}(X)=d_k(X)-d_{K-1}(X)$)
  其中($d_k(X)=\frac{(X-\xi_k)_{+}^3-(X-\xi_K)_{+}^3}{\xi_K-\xi_k}$) 现在笔者的问题是，这个基函数是怎么推导出来的，我还是没有搞清楚，如果有童鞋对此问题比较清楚地，可以指导我一下。
  如上的，就是自然三次样条的定义。我们下面通过一个实际数据的例子来看看如何用自然三次样条对实际问题进行分析。
  数据来自于网站：http://www-stat.stanford.edu/~tibs/ElemStatLearn/ 这个网站就是这本书的网站。这三位斯坦福的大牛把自己书的几次版本全都放在这个网站上，还有相应的数据，为读者练手提供了良好的条件。相当的靠谱。
  以下部分是数据的描述：

  A retrospective sample of males in a heart-disease high-risk region of the Western Cape, South Africa. There are roughly two controls per case of CHD. Many of the CHD positive men have undergone blood pressure reduction treatment and other programs to reduce their risk factors after their CHD event. In some cases the measurements were made after these treatments. These data are taken from a larger dataset, described in Rousseauw et al, 1983, South African Medical Journal. sbp systolic blood pressure tobacco cumulative tobacco (kg) ldl low densiity lipoprotein cholesterol adiposity famhist family history of heart disease (Present, Absent) typea type-A behavior obesity alcohol current alcohol consumption age age at onset chd response, coronary heart disease

  原谅我太懒，没有翻译这段文字。数据的响应是chd，是分类变量。输入中也有分类变量是famhist。我们先看看数据长什么样。
  按照惯例来说，我们都应该先画个图看看这对数据长得如何。
  图中不同颜色的点代表不同的类别。我们研究这些数据的目的在于，我们要找出哪些因素会导致心脏病，以及这些因素如何导致心脏病。这个图片太小，看得并不是很清晰。具体说明了什么问题，事实上我也并不很清楚。
  我们首先用logistic回归，对数据进行分类规则的学习。
  代码很简单：
  fit.glm<-glm(chd~.,data=heart,family=binomial())
  summary(fit.glm)
  step(fit.glm)
  利用逐步回归，拟合logistic回归模型。
  最终结果如下：
  从这个结果我们看到，logistic回归之后，再用逐步回归进行变量选择之后，最终的模型为
  $chd=-6.45+0.0804\times tobacco+0.16199\times ldl+0.90818\times famhis+0.03712\times typea+0.05046\times age$,
  这个模型的AIC=487.7。我们来看看这个用这个模型在原来训练样本上做分类的效果如何。
  我们计算得到，这个分类器分类的错误率是27.23%，还可以。
  这部分代码如下：
  pred.glm<-predict(fit.glm2)
  #head(pred.glm)
  #plot(pred.glm,heart$chd)
  length<-length(pred.glm)
  pred1<-rep(0,length)
  for(k in 1:length)
  {
  if(pred.glm[k]>0.5)
  {pred1[k]<-1}
  }
  head(pred1)
  error<-sum(abs(pred1-heart$chd))
  error.rate.glm<-error/length
  之后我们开始进入正题。我们知道logistic回归是线性分类器的一种，我们现在需要挖掘该分类规则中非线性的一些成分。这个模型的长的是这样的; ($logit\[P(chd|X)\]=\theta_0+h_1(X_1)^T \theta_1+h_2(X_2)^T \theta_2+\cdots+h_p(X_p)^T\theta_p$) 上面模型的每一个term我们都用四个自然样条基，比如说，($X_1$)代表sbp，($h_1(X_1)$)是一个包含了四个基函数的基。对于这个问题来说，一共需要估计的参数是4*9=36个，下面的代码实现了上述所说的内容。
  matrix<-as.matrix(heart[1:9])
  #matrix
  library(splines)
  matrix.spline<-ns(matrix,df=36)
  heart.splne<-data.frame(cbind(matrix.spline,heart$chd))
  #head(heart.splne)
  fit.spline<-glm(V37~.,data=heart.splne)
  summary(fit.spline)
  #step(fit.spline)
  pred.spline<-predict(fit.spline)
  pred.spline.1<-rep(0,length)
  for(i in 1:length)
  {
  if(pred.spline[i]>0.5)
  {pred.spline.1[i]<-1}
  }
  error.spline<-sum(abs(pred.spline.1-heart$chd))
  error.rate.spline<-error.spline/length
  现在的问题是，做完了这些应该做变量选择。可是这里变量选择就要涉及到分组变量选择了。虽然之前接触过一些分组变量选择的内容，但是实现起来仍然是有一定的困难。
  今天先这样，明儿再说。
  2011-11-03 16:43:38  1回应

• Kernel Methods

  本书第六章介绍了核方法（Kernel）。记得上高等数理统计的时候，老师布置过关于核方法的一片小论文作业，只不过当时并没有重视，作业也是应付了事。这两天读了这一章，觉得核方法是一种非常重要的工具。当然，这一章中也有众多地方读不懂，慢慢继续读吧。

  下面写点读书笔记和心得。
  6.1节，先从最基本的一维核平滑说起。
  所谓的平滑，我觉得可以这样理解。对于一维变量及其相应，可以在二维空间中画一个散点图。如果利用插值，将点连接起来，那么连线可能是曲折不平的。所谓的平滑，就是用某种手段使得连线变得平滑光滑一点。那么手段可以有多种，比如第五章介绍的样条平滑，是利用了正则化的方法，使得连线达到高阶可微，从而看起来比较光滑。而本章要介绍的核方法，则是利用核，给近邻中的不同点，按照其离目标点的距离远近赋以不同的权重，从而达到平滑的效果。
  下面比较详细的介绍
  之前介绍过k-最近邻方法，是用($\hat{f}(x)=Ave(y_i|x_i \in N_k/(x))$)作为回归方程($E(Y|X=x)$)的估计。
  上图显示的是一个利用最近邻方法对回归方程的估计。真模型是图中蓝色的线，绿色的曲曲折折的这一条就是用30最近邻方法对这个真模型的估计。可以看到，确实是非常的不平滑，而且也很丑，也是不必要的。下面图是利用了核平滑之后得到的结果，可以明显地看出来，拟合的曲线确实平滑了很多。
  上面仅仅是一个核平滑的例子。下面给出一维核平滑的一些具体的公式 ($\hat{f}(x_0)=\frac{\sum_{i=1}^N K_{\lambda}(x_0,x_i)y_i}{{\sum_{i=1}^N K_{\lambda}(x_0,x_i)}}$) 这个就是利用核平滑对($x_0$)点的真实值的估计，可以看出，这其实是一个加权平均，相比起最近邻方法，这里的特殊的地方就是权重($K_{\lambda}(x_0,x)$)。这个权重就称为核。
  核函数有很多种，常用的包括
  Epanechnikov quadratic 核：($K_{\lambda}(x_0,x)=D(\frac{x-x_0}{\lambda})$) with ($D(t)=\frac{3}{4}(1-t^2),|t|<1$)
  这个图就是($D(t)$)的图像，可以看出，随着离目标点的距离越来越远，所附加的权重也是平滑的越来越小。核函数的定义中($\lambda$)是所谓的窗宽（window width）。这个值限制了权重赋值的范围。比如说设置$\lambda=0.2$，对于上面的核函数而言，只有离目标点的距离（差的绝对值）小于等于0.2的点，才会被赋以一个正的权重，剩下的点的权重均为0，因此也就是说在加权平均的时候，只考虑这些点。
  更为一般的，窗宽我们认为是一个关于目标点($x_0$)的函数($h_{\lambda}(x_0)$)。那么，对于上面定义的Epanechnikov quadratic kernel，窗宽是一个常数($h_{\lambda}(x_0)=\lambda$)。而对于k-最近邻而言，($h_{\lambda}(x_0)=|x_0-x_{[k]}|$) Epanechnikov核具有紧支集。
  此外，还有比较流行的具有紧支集的核函数，based on tri-cube function：($D(t)=(1-t^3)^3$),当($|t|<1$)时，其他时候为0.
  可以看到，这个核函数的目标点处于中间部位的时候，所赋权重比较平缓，在边界处则非常的不同。
  另外，还有一个比较常用的核函数，是基于高斯密度的。这个核函数的支撑不紧。
  一般比较常用的就是如上所说的三种核函数。为了方便，在本笔记的后续部分，我们分别称之为E核函数，T核函数，G核函数。
  上面我们介绍了核方法，对于最近邻方法的一种修正。下面来看一看，在回归中如何利用核方法。事实上，即使用核函数加权，最近邻方法仍然是某种平均。在某一个邻域内仍旧是常量。回归方法相比来说，就显得更近了一步。
  局部加权线性回归是如下问题的解： ($min_{\alpha(x_0),\beta(x_0)}\sum_{i=1}^N K_{\lambda}(x_0,x_i)[y_i-\alpha(x_0)-\beta(x_0)x_i]^2$) 得到的估计值是($\hat{f}(x_0)=\hat{\alpha}(x_0)+\hat{\beta}(x_0)x_0$) 当我们用向量和矩阵的形式表达上面的式子之后，我们发现，这个估计值对于($y$)来说，确实是线性的。($\hat{f}(x_0)=\sum_{i=1}^Nl_i(x_0)y_i$) 对于这个式子中的($l_i(x_0)$)，它是结合了核以及最小二乘算子的，有的时候，这个东西也被称为equivalent kernel。相当于是对响应($y$)赋权重。
  之所以要引入局部线性回归，主要的原因是局部的加权平均值在边界处非常不稳定，而局部线性回归则将这个不稳定的因素自动的限制在了一阶，这个现象又称为automatic kernel carpentry。这部分用到了泰勒展开，具体的推到原书中写得比较详细。
  有了局部线性回归，就自然可以推广到局部多项式回归。这里也不赘述。
  值得一提的是，虽然阶数越高，偏差越小，但是方差会增大。在选择模型的时候，需要进行权衡。此外，局部多项式回归在边界处方差比较大。
  （插进一腿，请区分：核平滑与局部回归。其实就是一个概念辨析）
  以上的讨论都是在x是一维的情况下进行的。下面讨论在p维下的推广。通常在p维情况下，核函数为一个径向函数（radial function）比如p维的E核函数或者T核函数，($K_{\lambda}(x_0,x)=D(\frac{||x_0-x||}{\lambda})$)，事实上里面的范数也可以有多种选择。
  对于多维的局部回归或者核平滑，条件散点图是一种可视化的好手段。
  本书第四节介绍了结构化的回归方法，我在阅读的过程中，对“结构化”并不怎么理解。因此，这一节读来也没什么心得，因此这里也不写什么了。
  第五节，介绍了局部似然核一些其他的模型，感觉挺靠谱的。介绍一下。
  首先要介绍的概念是变系数模型，这个模型与之前提到的条件散点图是相关的。不同条件下，自变量和响应之间拟合的模型不同，这个模型的系数是随着条件变化的，因此叫做变系数模型。书中提到了一句话“any parametric model can be made local if the fitting method accommodates observation weights”。
  比如说，很多似然模型，也就是基于极大似然估计得到的模型，也可以引入核，对于每一个观测($y_i$)，都有一个参数($\theta_i=\theta(x_i)=x_i^T\beta$)，而($\beta$)则是基于对数似然的($l(\beta)=\sum_{i=1}^N l(y_i,x_i^T\beta)$)，当我们要预测某一个点局部的参数值的时候，就可以用($l(\beta(x_0))=\sum_{i=1}^n K_{\lambda}(x_0,x_i)l(y_i,x_i^T\beta(x_0))$)。
  便是所谓的局部似然。
  当然在时间序列做自回归模型的时候，也可以引入核，这一点我记得在我关于时间序列的笔记中有介绍过，这一点就不再赘述了。
  至此，我们已经介绍了核方法的三个方面的应用，一是核平滑，二是局部回归，三是局部似然以及其他模型。下面介绍另外一种非常常用的，核密度估计。
  比如说我们有N个点，从某一个概率密度函数($f_X(x)$)中随机抽取的，我们希望能够估计某一个点($x_0$)处的密度值($f_X(x_0)$)。那么一个自然而然的估计是：($\hat{f}_X(x_0)=\frac{the~ number~ of ~x_i \in N(x_0)}{N \lambda}$)。当然这个想法是比较原始的，更进一步，我们的估计可以更加平滑一些($\hat{f}_X(x_0)=\frac{1}{N\lambda}\sum_{i=1}^N K_{\lambda}(x_0,x_i)$)。这个更加的平滑，叫做smooth Parzens estimate。这个利用核估计谜底的情况下，通常选用的是高斯核函数。
  有了核密度，我们可以直接套bayes公式来做分类问题， ($P(G=j|X=x_0)=\frac{\hat{\pi_j}\hat{f_j}(x_0)}{\sum\hat{\pt_k}\hat{f_k}(x_0)}$)
  （这又是一种分类器。似乎已经读到了不少分类器，应该适时的总结一下不同的分类器了。）
  本书的6.6.3节介绍了一种相当重要的分类器，Naive Bayes Classifier。当维度比较高的时候，这个分类器比较实用。这个模型假设，给定所属类别，不同变量之间是独立的。因此，在给定类别的条件下，边际密度可以单独估计，之后得到变量的联合密度，然后利用Bayes公式计算后验概率密度，得到分类的结果。这种方法似乎是非常非常常用。应该值得注意。
  至此，已经介绍了利用核密度估计来分类以及利用Naive Bayes方法分类。其不同点在于对自变量联合概率密度的估计方法不同。那么，还有一种非常常用的分类方法，是利用混模型（Mixture Models）：($f(x)=\sum_{m=1}^M \alpha_m \phi(x;\mu_m,\Sigma_m)$),混模型中最常用的是高斯密度，通常来说系数是利用极大似然估计的。有了混模型，我们可以估计观测落在某一个分布下的概率：($\hat{r_{im}}=\frac{\hat{\alpha}_m \phi(x_i;\hat{\mu}_m,\hat{\Sigma}_m)}{\sum_{k=1}^M\hat{\alpha}_m \phi(x_i;\hat{\mu}_k,\hat{\Sigma}_k}$) 设定某个阈值，我们就可以做分类了。
  这又是一种分类的方法。目前为止，已经接触到的分类方法包括线性回归，判别分析，logisitic回归，用了样条的logistic回归，利用核密度做分类，Naive Bayes分类器，还有就是混模型分类吧，今后专门总结一下，然后写一篇笔记。
  2011-11-16 20:15:50  回应

• 第201页

  这一章看得太费劲了，笔记得一点儿一点儿写。现在就单写201页的这张图。图中的红线，是预测误差，绿线是偏差的平方，蓝线是方差。
  对于回归问题，预测误差是由偏差和方差相加得到的。但是对于分类问题，下面的两张图，偏差和方差与上面两张图相同，但是预测误差不一样。为什么会出现这种情况？
  因为对于分类问题，让我们留在正确分类的区域所产生的估计误差并不hurt。
  这个图算是比较经典解释了不同的损失函数下的，误差，方差以及预测偏差之间的关系。值得关注。
  2011-11-24 16:33:24  回应

• 第七章 模型评估与选择

  这一章的内容是模型评估与选择，断断续续看了两周时间，感觉比看模型还费劲。其实这一章的大部分内容我是熟悉的，包括各种模型选择的准则，交叉验证以及bootstrap，这些在实际建模的时候也经常用到，但是关于其原理确实不是很清晰。这一章给出了详尽，但是又不那么理论的阐述。经典确实是经典。闲话不多说了，开始读书笔记。

  对于同一个问题，比如分类问题或者预测问题，往往会有一系列的模型都可以做。那么这些模型表现的如何，如何从这些模型中选择一个合适的，最好的模型，就成为了一个问题。而这个问题在实际中是非常重要的。我们都知道，模型是建立在训练样本上的，而预测是需要在一个独立的新的样本上进行的。在训练样本上所建立的模型，其在一个新的独立的样本上的表现如何进行评估，是一个非常重要的问题。
  这一章首先介绍了偏差（bias），方差（variance）以及模型复杂度（model complexity）。我们有一个target variable Y，以及输入向量X，以及通过训练样本得到的对于响应的估计（也就是我们的模型）($\hat{f}(X)$)。此外，我们还应该有一个损失函数($L(Y,\hat{f}(X))$)。损失函数可以有多种选择，比如平方损失，绝对值损失，这两个主要是针对定量的响应的，对于定性的响应，也有0-1损失，对数似然之类的。一般而言，损失函数中比较常用的就是这些。
  有了模型以及损失函数之后，首先定义test error（原谅我在这里中英混杂，因为我发现用这种方法可以更好地区分几个不同的概念）。test error是损失函数在一个新的，独立的检验样本上的期望。($Err=E[L(Y,\hat{f}(X))]$)。这个期望的计算需要涉及到新的检测样本的联合分布。
  以上是test error的概念。于此对应的是training error的定义，training error是指在训练样本上的损失的平均值。($\bar{err}=\frac{1}{N}\sum_{i=1}^N L(y_i,\hat{f}(x_i))$)
  上面的图综合的阐述了模型复杂度，偏差，方差之间的关系。从图中，我们可以看出，training error显然不是test error的一个好的估计。显然，training error都低估了test error。这个原因很容易解释，training error所用的数据依然是建立模型用的数据，当然误差要小。另外，从这张图可以看出，随着模型复杂度的增加，training error是再不断减小的，而且如果模型足够复杂，是不会有training error的。这种现象，往往被称为过拟合。也就是说，拟合的太过头了。这也不是一个好现象。
  我们想要评估一个模型的好坏，想要知道的，肯定是test error。通常而言，我们对于解决某个问题，会有一族模型，这族模型有一个tuning parameter ($\alpha$)。我们记这族模型为($\hat{f}_{\alpha}(x)$)。通常这个tuning parameter是用以辨识模型复杂程度的。
  这一章的主要任务是估计test error曲线。而通常的模型选择和评估大致分为两个步骤，先通过training error来选择模型，然后再通过test error评估模型。
  对于test error的估计，通常有两种策略。一种是解析的做法，比如AIC，BIC之类的。另外一种则是用交叉验证（cross-validation）或者bootstrap来估计。这两类方法也是本书这一章的主要的内容构成。
  在介绍这些方法之前，有必要先看一看bias-variance分解。($Err(x_0)=\sigma_{e}^2+Bias^2(f(x_0))+Variance$) 通常而言，模型越复杂，bias越低，而方差variance则越高。关于这一部分，在之前的一篇笔记中已经通过一个图提到了，这里也不再详述。
  通常，training error都是小于test error的。Err在某种意义上是extra-sample error。若我们定义in-sample error，则training error对于test error的乐观估计则更好理解。
  in-sample error的定义是($Err_{in}=\frac{1}{N}\sum L(Y_i^{new},\hat{f}(x_i))$)。则这个估计的乐观的部分如下定义 ($op=Err_{in}-E_y(\bar{err})$) 而通过推到，我们可以得到（这个推到书上也没有，应该是某一系列论文中的成果，我们这里不具体推，只要知道这个结果就行） ($Err_{in}=E_y(\bar{err})+\frac{2}{N}\sum cov(y_i,\hat{y}_i)$) 这个结果揭示了一个很重要的事儿，就是乐观估计的程度与估计值和真实值之间的相关性是密切相关的。
  写到这我也有点糊涂了，按理说，我们需要的是test error的估计，而现在，我们只需要来估计in-sample error了。作者在这里说了一句话，

  “In-sample error is not usually of direct interest since future values of the features are not likely to coincide with their training set value.But for comparison between models,in-sample error is convenient and often leads to effective model selection”

  。那么我们就按照作者的经验，来开始对in-sample error进行估计吧。
  对于in-sample error的估计，有两个不同的角度可以进行，一种是估计op，然后加到($\bar{err}$)上即可。这也就是AIC，BIC的思路。另外一种就是利用重抽样，比如cross-validation或者bootstrap的策略，来估计in-sample error。下面的部分，就分别比较详细的介绍一下这些方法。
  ($C_p$)统计量： ($\hat{Err}_{in}=\bar{err}+\hat{op}$) 是通用的一个式子，不同的准则有对这个式子不同的估计，我们先来看最常用的($C_p$)准则。 ($C_p=\bar{err}+2\frac{d}{N}\sigma_{e}^2$) 这个公式适用于加法模型，而且如果估计值是线性的情况下。
  AIC准则： ($AIC=-2Loglik+2\frac{d}{N}$).
  当损失函数对数似然损失函数的时候，这个准则比($C_p$)准则更加广义。其所依赖的理论是一个大样本性质，当N趋于无穷大的时候， ($-2E[log Pr_{\hat{\theta}}(Y)] \sim -\frac{2}{N}E[loglik]+2\frac{d}{N}$) 其中($loglik=\sum log Pr_{\hat{\theta}}(y_i)$) 用AIC准则进行模型选择的时候，是选择AIC越小愈好。这一部分书中有一个简单的例子，但是很能说明问题，不在此多说了。
  BIC准则： ($BIC=-2loglik+(logN)d$) BIC准则的得来的motivate是非常不同的，选择BIC最小的模型，事实上是在选择后验概率最大的模型。BIC准则的得来，是通过bayes理论推导得到的。这里在书中也有具体的公式推导。
  MDL：
  minimum description length。这个部分，我几乎没怎么看明白，其核心是编码理论。
  以上是一些模型选择的准则。模型选择的准则都涉及到了模型有效参数的个数，因此，这一章也对这个问题做了一些讲解。包括7.6the effective number of parameters以及7.9的Vapnik-Chernovenkis dimension，都是主要讲了模型复杂度的度量。这两部分的内容我看的并不是很清晰，也没什么感觉。希望再读此书能有所收获。这次阅读，这部分我都略过了。
  以上的一些准则，都是对op的一个比较解析的估计。下面介绍两种通过重抽样的策略，来估计in-sample error的方法。
  cross-validation： ($CV=\frac{1}{N}sum_{i=1}^N L(y_i,\hat{f}^{-k(i)}(x_i))$) 交叉验证，就是把训练样本大致平均地分成K分，然后每次剔除一部分，用另外的部分进行模型构建，然后用剔除的那一部分来估计误差，这样做K次，然后平均K次的误差。
  通常而言，都是用5-cross validation或者10-cross validation。当然还有每次剔除一个值，leave-one-out。如何选择K是一个问题，当K=N的时候，CV是预测误差的渐进无偏估计。但是方差可能会很大。当K比较小的时候，方差会比较小，但是偏差比较大，也是一个问题。作者说

  "over-all five or ten fold cross-validation are recommended as a good compromise"

  。拿来用用，比一比即可。
  bootstrap方法：
  这一部分我不想多说，在豆瓣里我有分享过关于bootstrap的相关资料。bootstrap这个方法最早就是stanford的Efron提出的，在模型选择中应用非常广泛，但是我个人还是比较喜好cross-validation的策略一些。
  差不多今天就到这了，这本书啥时候才能看完啊。
  2011-11-28 16:17:30  4回应

• 第八章 模型推断和模型平均

  这一章的题目叫做model inference and averaging。直译过来是模型推断和模型平均。这一章断断续续看了也有一周时间，只可惜平日里在这方面无甚积累，写不出来什么。今天的读书笔记只好瞎白活两句了。部分内容与本章所讲有关，部分是我平日里关于统计的一些思考。

  统计学在南开，是放在数学院下面。比较偏重统计的数理方面，重理论。上了硕士以后，直接接触的都是试验设计的东西，关于统计学习或者统计建模方面的文章，读来也都是为设计服务，看看有木有一个好的设计能改进某个模型的精度的。由于本人个人专业方向的原因，对于bayes的一些东西了解的不够，对于非参的东西了解的也不够。直接导致了我对于第七章，第八章（尤其是第八章）内容的不适用。在上高等数理统计的时候，院长给我们布置了很多当时看起来很诡异的课后作业，包括自学bootstrap，核方法等等。都是交小论文，读过Efron的那本关于jackknife和bootstrap的小册子，也读过不少核方法的论文，因为当时没有怎么用心，而且当时的英文程度也不行，因此也就没什么收获。如今读到这本书，觉得当时真是蹉跎了岁月。
  这一章的内容充满了斯坦福的味道，尤其是本章后半部分内容，基本上都是Tibs的成果。包括model averaging方面的一些方法，比如bumping，看了看，确实是一种很好的提高估计精确度的策略。之前却对此毫无耳闻。第十章专门介绍boosting方法，这种方法经常见到，应用较广。因此对于本章介绍的方法，我也仅仅是大致扫了几眼，没在深究。
  我觉得，本章比较有意思的内容，是前半部分，关于bootstrap和极大似然，最小二乘之间的关系。其本质上是bootstrap方法的大样本理论。南开这两年因为邹老师的缘故，在大样本这方面建树颇多，虽然我依然对其理论不熟悉，但是同宿舍有这方面的专家，随便讲解几句，心里也了然很多。
  第八章的内容事实上是延续了第七章的内容，是做模型实务的非常好的参考。
  看了这一章的内容之后，我对于bootstrap方法多了很多认识，这种方法真的非常不错，从其大样本的性质来讲也好，从其可计算性来讲也好。以后要重视对这种方法的应用。
  另外，本章介绍了EM算法和Gibbs抽样。EM算法，学过，可是从来也没自己编程实现过，而MCMC的内容，也非常的不熟悉。
  第七章和第八章就这样吧，接着看第九章，树的内容。还有支持向量机，以及无监督的几种学习算法，争取在一个月之内，把本书剩余部分搞掉，然后开始看MCMC的书。
  看一天书，倍儿累。嗓子眼儿堵堵的，看书看费劲了我就这德行了。
  儒林重新开业，昨儿去定了现在看的这本书。这本书确实非常经典，有必要收藏，顺手买了Monte Carlo Statistical Methods，瞬间穷了。
  儒林在南开的重新开业，让我这个临近毕业的人稍微有所慰藉。
  2011-11-29 16:16:25  回应

• 第九章 一些模型（1）

  第九章的内容，介绍了一些比较高级的模型，连续在资料室苦读了两天，终于把内容大致过了一遍。这些模型的R包也基本上找出来，并实例演练了一下。感觉收获非常多。下了相关的参考文献，又是一大堆。准备回头具体看看吧。老外写这种专业性质的书，都是属于百科全书式，引导读者去读文献，书中的内容，因为省略了大量的步骤，因此有时会感到有些费解。不过如果纯粹从应用的角度去看到话，知道原理，用在何处，如何用，如何解读大致的结果，似乎也就够用了。

  对于第九章，我决定写三篇读书笔记，这是第一篇，主要是小结广义可加模型。第二篇准备介绍树（CART）以及相关的（prim，HME），第三篇则重点介绍Friedman的MARS（带我读完其参考文献之后详细点写).先给自己定这些目标，然后慢慢去看吧。
  本学期还剩下不到一个月结束，务必先把这本书看完。
  下面进入正题，开始简单介绍广义可加模型。
  广义可加模型的优点是more automatic flexible，当然这是相比起传统的线性模型而言的。也就是模型更加灵活，因此对非线性性的识别和探索上比较有优势。其模样如下：
  ($E(Y|X_1,X_2,\ldots,X_p)=\alpha+f_1(X_1)+f_2(X_2)+\cdots+f_p(X_p)$)
  其中($f_j$)是未知的，非参函数，也就比较平滑。对于每个这样的函数，都用scatterplot smoother来拟合。（这里不知道这个词具体怎么翻译，但是意思就是，拟合的方法是某种平滑方法，比如三次平滑样条，或者核平滑之类的，之前的笔记中介绍过），这个模型的构建的另外一个特别之处，在于提供了一种同时估计p个函数的一种算法。这都是相对于以前的传统的模型的区别。
  上面的这个广义可加模型的样子，事实上只体现出来了可加，而所谓的广义，与广义线性模型中的广义意思差不多，指的是响应所服从的分布，比如可加的logistic回归模型，就是长成下面这个样子：
  ($log(\frac{\mu(X)}{1-\mu(X)})=\alpha+f_1(X_1)+\cdots+f_p(X_p)$)
  和广义线性模型一样，这边就涉及到了link function，link function和广义线性模型（glm）中的都类似。
  关于方程($f_j$)的估计，是比较flexible的，所用的算法，其构成的基础元素是scatterplot smoother。估计得到的($\hat{f}_j$)可以挖掘出($X_j$)的效应中的非线性的成分。当然了，并非所有的($X_j$)的函数都必须是非线性的。我们可以使用半参数模型。
  事实上，传统的线性模型，只是广义可加模型的一种特例。这一点也就让我们充分意识到广义可加模型的重要地位。（在这里又要发表一下小小的感慨，stanford对统计学的贡献真是高山仰止）。
  以上介绍了广义可加模型的定义，以及大致粗浅介绍了其拟合模型的算法思想。下面比较具体的（但是也没有太多具体推到）介绍如何拟合一个可加模型。
  将要介绍的算法是一种通用的方法。为了比较方便叙述，我们这里选用的scatterplot smoother为三次平滑样条。可加模型是：
  ($Y=\alpha+\sum_{j=1}^p f_j(X_j)+\varepsilon$)
  误差项($\varepsilon$)均值为0。
  我们定义一个损失函数：
  ($PRSS(\alpha,f_1,f_2,\ldots,f_p)=\sum_{i=1}^N{y_i-\alpha-\sum_{j=1}^p f_j(x_{ij})}^2+\sum_{j=1}^p \lambda_j \int f_j^{''}(t_j)^2dt_j$)
  ($\lambda_j$)是tuning parameters。可以证明（书中并没有证明，具体如何证明，徐参看参考文献，我没看过参考文献，纯从应用的角度考虑，可以不用管这是如何证明的），最小化PRSS得到的解是一个可加三次样条模型。每一个函数($f_j$)是一个关于($X_j$)的三次样条，每一个不同的值($x_{ij}$)都是结点（knot），($i=1,2,\ldots,N$)。
  这个模型显然不是唯一的（因为有常数项，可以对后面的可加项进行调节），为此，我们必须再增加一点限制，使得输入变量的矩阵必须是非奇异的，才能保证求解是唯一的。通常选用的限制是($\sum_{i=1}^Nf_j(x_{ij})=0$),对所有($j$)都成立。
  对于这个问题的求解算法，需要用到一个简单的迭代。下面我试图用语言，而少用公式。看看能不能将其表述清楚。
  一开始，我们就设定($\hat{\alpha}=\frac{1}{N}\sum_{i=1}^N y_i$)，并且这个值以后都不改变了。我们对($\{y_i-\hat{\alpha}-\sum_{j \neq k} \hat{f}_j(x_{ij)}\}_1^N$)这些点，拟合一个三次平滑样条($S_k$)，这个三次平滑样条相当于是($x_{ik}$)的一个函数($\hat{f}_k$)。对于每个输入变量，这个是轮流进行的。直到我们得到的估计值($f_j$)比较稳定了，不怎么变化了。这种算法的名称叫做backfitting。算法如下：
  这个算法中($S_j$)可以换成其他smoother，比如局部回归，或者核方法。
  对于logistic回归模型而言，一个类似PRSS的，更为合适的准则应该为带有惩罚项的对数似然，要使其最大化，用到了Newton-Raphson算法，具体的算法细节，书中没有介绍，但是推荐了Hastie和Tibshirani（1990）专门介绍广义可加模型的书。回头有机会也要认真读读。
  关于广义可加模型的介绍部分到此为止，自己之前也没研究过这方面的文章，因此不甚了解，只是知道一个大意，看完这部分内容也是仅仅知道大意。下面介绍R中专门做广义可加模型的package VGAM。
  先分享一张图片，是这个包的作者在2011年中国R会议上海分会场上作报告的ppt中的一张图
  这种图讲清了各种回归模型的脉络。相当的值得收藏。
  下面简单介绍这个包。这个包里核心的函数有三个，vglm(),vgam(),rrvglm()。第三个是降秩的。具体如下：
  给大家一个下载此ppt的链接：http://cos.name/2011/11/4th-china-r-shanghai-summary/ 感兴趣的同学可以去看看。
  昨天用vgam试了试，本书上的关于垃圾邮件的数据，可是有个问题一直也没解决。目前正在写信咨询这个包的原作者。有了结果，会更新这篇读书笔记。
  今天就这样。
  _________华丽的分割线——————————————
  晚上又上网搜了搜关于广义可加模型一些软件实现。SAS可以实现广义可加模型，具体参见：http://support.sas.com/rnd/app/da/new/dagam.html 另外，我之前的文章中用的是VGAM，事实上在R中，有一个gam包，直接是做广义可加模型的，这也是我晚上在斯坦福统计系主页上随便逛逛才发现的。VGAM事实上是vector gam，而gam这个包应该是更贴切的，也是我更需要的。gam包的作者就是Hasite大神。这才是见到了本宗啊。
  学起来
  --------再次华丽的分割----------
  之前提到的问题已经圆满解决，经过统计制度邱同学的提醒，我已经解决了太长的公式不好分别写出的问题。下面把R代码贴过来，以供有需要的同学使用。
  诀窍就是用paste和as.formula

  > setwd("F:/Data Mining/Machine Learning/spam")
  > mydata<-read.table("data with name.txt",header=TRUE)
  > varsname<-names(mydata[-58])
  > #varsname
  > for(i in 1:length(varsname))
  + {
  +   varsname[i]<-paste("s(",varsname[i],sep="")
  +   varsname[i]<-paste(varsname[i],")",sep="")
  + }
  > varsname
   [1] "s(word_freq_make)"             "s(word_freq_address)"         
   [3] "s(word_freq_all)"              "s(word_freq_3d)"              
   [5] "s(word_freq_our)"              "s(word_freq_over)"            
   [7] "s(word_freq_remove)"           "s(word_freq_internet)"        
   [9] "s(word_freq_order)"            "s(word_freq_mail)"            
  [11] "s(word_freq_receive)"          "s(word_freq_will)"            
  [13] "s(word_freq_people)"           "s(word_freq_report)"          
  [15] "s(word_freq_addresses)"        "s(word_freq_free)"            
  [17] "s(word_freq_business)"         "s(word_freq_email)"           
  [19] "s(word_freq_you)"              "s(word_freq_credit)"          
  [21] "s(word_freq_your)"             "s(word_freq_font)"            
  [23] "s(word_freq_000)"              "s(word_freq_money)"           
  [25] "s(word_freq_hp)"               "s(word_freq_hpl)"             
  [27] "s(word_freq_george)"           "s(word_freq_650)"             
  [29] "s(word_freq_lab)"              "s(word_freq_labs)"            
  [31] "s(word_freq_telnet)"           "s(word_freq_857)"             
  [33] "s(word_freq_data)"             "s(word_freq_415)"             
  [35] "s(word_freq_85)"               "s(word_freq_technology)"      
  [37] "s(word_freq_1999)"             "s(word_freq_parts)"           
  [39] "s(word_freq_pm)"               "s(word_freq_direct)"          
  [41] "s(word_freq_cs)"               "s(word_freq_meeting)"         
  [43] "s(word_freq_original)"         "s(word_freq_project)"         
  [45] "s(word_freq_re)"               "s(word_freq_edu)"             
  [47] "s(word_freq_table)"            "s(word_freq_conference)"      
  [49] "s(char_freq_.)"                "s(char_freq_..1)"             
  [51] "s(char_freq_..2)"              "s(char_freq_..3)"             
  [53] "s(char_freq_..4)"              "s(char_freq_)"                
  [55] "s(capital_run_length_average)" "s(capital_run_length_longest)"
  [57] "s(capital_run_length_total)"  
  > (fmla<-as.formula(paste("y~",paste(varsname,collapse="+"))))
  y ~ s(word_freq_make) + s(word_freq_address) + s(word_freq_all) + 
      s(word_freq_3d) + s(word_freq_our) + s(word_freq_over) + 
      s(word_freq_remove) + s(word_freq_internet) + s(word_freq_order) + 
      s(word_freq_mail) + s(word_freq_receive) + s(word_freq_will) + 
      s(word_freq_people) + s(word_freq_report) + s(word_freq_addresses) + 
      s(word_freq_free) + s(word_freq_business) + s(word_freq_email) + 
      s(word_freq_you) + s(word_freq_credit) + s(word_freq_your) + 
      s(word_freq_font) + s(word_freq_000) + s(word_freq_money) + 
      s(word_freq_hp) + s(word_freq_hpl) + s(word_freq_george) + 
      s(word_freq_650) + s(word_freq_lab) + s(word_freq_labs) + 
      s(word_freq_telnet) + s(word_freq_857) + s(word_freq_data) + 
      s(word_freq_415) + s(word_freq_85) + s(word_freq_technology) + 
      s(word_freq_1999) + s(word_freq_parts) + s(word_freq_pm) + 
      s(word_freq_direct) + s(word_freq_cs) + s(word_freq_meeting) + 
      s(word_freq_original) + s(word_freq_project) + s(word_freq_re) + 
      s(word_freq_edu) + s(word_freq_table) + s(word_freq_conference) + 
      s(char_freq_.) + s(char_freq_..1) + s(char_freq_..2) + s(char_freq_..3) + 
      s(char_freq_..4) + s(char_freq_) + s(capital_run_length_average) + 
      s(capital_run_length_longest) + s(capital_run_length_total)
  

  muhaha
  2011-12-02 21:04:59  回应

• 一些模型（2）

  继续第九章的读书笔记，这次的读书笔记主要内容为基于树的模型（tree-based methods）以及相关的两个模型，prim以及HME。

  我越是看这本书，越觉得我硕士的前两年真是白念了。如果这本书我早一年或者一年半遇到，并且开始阅读的话，这一年多的时间，我应该足够参与更多的比赛，拿更好的名次和奖励。每次读这本书，都觉得确实相当之经典。此外，看着我已经写了九章的读书笔记，书已经读了10章多，马上就要读完它。还是觉得小有成就感的。最后一年的学生生活（其实只剩下半年不到就要毕业），且行且珍惜吧。
  开始正题，开始介绍基于树的模型。主要是介绍分类树与回归树（classification and regression tree，CART），关于其他树结构的算法比如C4.5之类，这里不介绍。R里做CART有两个包，tree和rpart，里面的函数都蛮好用。
  具体介绍一下分类树与回归树的背景，也就是这种方法的大致想法。
  用上面这个图举一个很简单的例子，分类树事实上就是把输入变量的空间切分为不同的部分，每个部分归为一类，从而达到分类的结果，也就是如下的一个分类树：
  分类树的大致意思就是这么个想法，想法很简单，关键是如何找到分类的变量，以及分类的那个值。split point的选取是关键。也就是如何生成一棵树的问题。下面先来看看回归树的生长（分类树其实就是响应是分类变量的回归树）：
  我们的数据，输入变量是p维的，一共有N个观测：($(x_i,y_i)$),($i=1,2,\ldots,N$),其中($x_i=(x_{i1},x_{i2},\ldots,x_{ip})$)。生长树的算法应该能够自动的确定splitting variables以及split points，以及这棵树的拓扑结构。假设我们已经把输入变量空间分割为了M个区域($R_1,R_2,\ldots,R_M$),每个区域的响应都是一个常量($c_m$)，则模型为： ($f(x)=\sum_{m=1}^M c_m I(x \in R_m)$)
  如果我们选用的准则为最小化残差平方和，则最好的对($c_m$)的估计是($\hat{c_m}=ave(y_i|x_i \in R_m)$)。
  但是这样看起来，要搜到最优的解似乎是不可能的，（因为这里涉及到很多的选择问题，比如选择分为多少个区域，如何选择分叉的点等等问题）
  因此，在生成一棵树的时候，选用的是贪心算法：
  首先，我们使用所有的数据，然后考虑某个变量j以及这个变量的某个值s，定义一对半平面（half-planes）：
  ($R_1(j,s)=\{X|X_j \leq s\}$)以及($R_2(j,s)=\{X|X_j > s\}$)
  然后我们开始搜，j和s，使得：
  ($min_{j,s}[min_{c_1} \sum_{x_i \in R_1(j,s)}(y_i-c_1)^2+min_{c_2} \sum{x_i \in R_2(j,s)}(y_i-c_2)^2]$)。
  对于每一个变量，点s都可以很快的找到。
  找到了最好的分割点，我们就把输入空间分割成为两部分，在每一个部分上再重复同样的算法，继续下去。
  如果我们一直继续下去，会生成一颗非常大的树，这棵树就回overfit，因此没有什么价值。那么决定生成一颗怎样体量的树就成为了很重要的话题。树的大小，就是模型的tuning parameter。这涉及到剪枝的话题。关于剪枝，也是一个很重要的话题，但是这里不多介绍了。
  以上就是回归树的大致的生成方法，于此响应的又分类树，分类树与回归树的主要区别在于响应变量属于分类变量，另外在于可以选用不同的准则，比如gini系数，cross-entropy之类的。关于分类树，这里不再多说什么。
  感兴趣具体实现的同学，可以去看R里面rpart包以及tree包，这两个包写的比较详细。
  关于基于树的模型，先写这么多，下面写点与之相关的其他的模型：
  第一个，PRIM。这个模型的具体算法我并没有搞太明白，R里有prim包，可以做这个算法。下面的图大致表明了这个算法的过程，就像一个不断挤压箱子，挤掉不符合条件的点，留下符合条件的点，然后边界就成为了分类的边界，大致是这样一个过程。
  第二个，HME（有点像遗传算法）
  这个算法相比CART更加灵活，而且有点bayes的味道，它最后给出的不是确切地分为那个类别，而是给出了一个概率，落入该类别的概率。具体算法参看原书吧。
  这两个模型之所以介绍的非常简略，主要是因为之前并未接触过，而书中写的也相对简略，没有看过参考文献，也写不出什么东西出来。回头具体研究一下算法，在我的分类器总结性文章中介绍，并加以实例（这个是我假期的计划）。
  今天就这样。