机器学习算法笔记Ⅳ——主成分分析原理及应用

PCA 算法简介

主成分分析（英语：Principal components analysis，PCA）是在不损失或者不很损失原始数据信息的情况下将一个多维数据进行降维处理，其中降维有两个目的：
◆减少输入信息，突出特征信息，提高运算效率
◆在一定程度上能消除数据中的冗余信息，增强数据的鲁棒性

解释一：
主成分分析是一种统计方法，通过正交变换将一组可能存在相关性的变量转换成一组线性不相关的变量，达到压缩的目的。【解释来源MOOC】
解释二
主成分分析可以看成一种坐标变换，在原始的坐标基上数据与数据之间存在一定相关性，通过主成分分析，将这些数据映射在一个新的坐标系中（即变换出一种新的正交基，新的正交基的维度往往小于原始坐标系中的正交基，因此在新的坐标系中能达到降维的目的），在新的坐标系中数据与数据之间线性无关。通过数据之间的无关性便能更好的进行分类，例如下图中，原始坐标系为二维笛卡尔坐标系，正交基为$i$、$j$即传统的$x$、$y$轴的单位向量，而新的坐标系为单个轴（可以看为数轴），其正交基只有一个即$e$。【解释来源我自己】

二维数据一维映射示例

举个栗子：在学生的考试中，往往有很多门功课的成绩。最简单的比较成绩好坏的方式就是算总分并进行排名。因此这就是一种最常见的降维方式，将多门功课的成绩降为一个总分成绩。但是，通过降维后的数据也有一个特点就是不能知晓原始信息之间的关系，比如看到一份总成绩的排名名单我们是无法推敲其各科成绩的。当然这里对降维算法的描述并不是特别准确和科学，具体的理解应在后面的原理解析中。这里只是简单介绍一下降维的优点。降维是PCA不可缺少的部分。

eyes up stay sharp 一波公式原理来袭

相关矩阵原理

特征值与特征向量

一般地，设A为$n$阶方阵，如果存在数$\lambda$和$n$维非零向量$\alpha$，使$$A\alpha =\lambda \alpha$$
则称$\lambda$为方阵A的一个特征值，$\alpha$为方阵A对应于特征值$\lambda$的一个特征向量。
例如：

$$A=\left(\begin{array}{cc}3& -2\\ 1& 0\end{array}\right),{\alpha }_1=\left(\begin{array}{c}1\\ 1\end{array}\right),{\alpha }_2=\left(\begin{array}{c}2\\ 1\end{array}\right),\beta =\left(\begin{array}{c}-1\\ 1\end{array}\right)$$有$$A{\alpha }_1=\left(\begin{array}{cc}3& -2\\ 1& 0\end{array}\right)\left(\begin{array}{c}1\\ 1\end{array}\right)=\left(\begin{array}{c}1\\ 1\end{array}\right)=1\left(\begin{array}{c}1\\ 1\end{array}\right)=1{\alpha }_1,$$$$A{\alpha }_2=\left(\begin{array}{cc}3& -2\\ 1& 0\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)=\left(\begin{array}{c}4\\ 2\end{array}\right)=2\left(\begin{array}{c}2\\ 1\end{array}\right)=2{\alpha }_2,$$$$A\beta =\left(\begin{array}{cc}3& -2\\ 1& 0\end{array}\right)\left(\begin{array}{c}-1\\ 1\end{array}\right)=\left(\begin{array}{c}-5\\ -1\end{array}\right)\ne \lambda \left(\begin{array}{c}-1\\ 1\end{array}\right)\ne \lambda \beta ,$$
●由定义可知，1和2就是A的两个特征值，${\alpha }_1$和${\alpha }_2$就是A分别对应于特征值1与2的特征向量；而\beta则不是A的特征向量。
●从几何的角度观察可以发现如果$\alpha$是A的特征向量，那么$A\alpha$相当于对$\alpha$做一定的“伸缩变换”。

正定矩阵与正交向量

定义1：如果任一非零实向量X，都使得二次型$f(X)=X^{T}AX>0$，则称$f(X)$为正定二次型，$f(X)$的矩阵A为正定矩阵，其中还有以下延申：
如果$f(X)=X^{T}AX<0$，则称$f(X)$是负定二次型；
如果$f(X)=X^{T}AX\ge 0$，则称$f(X)$是半正定二次型；
如果$f(X)=X^{T}AX\le 0$，则称$f(X)$是半负定二次型；
不是正定，半负定，负定，半负定的二次型统称为不定二次型。

推论1：如果A为正定矩阵，那么其特征值全部为正数，如果A为非负定矩阵即A为正定矩阵或半正定矩阵，其特征值全部非负。同理，如果如果A为非正定矩阵即A为负定矩阵或半负定矩阵，其特征值全部非正。

两个向量正交，则两个向量的乘积为零向量

PCA 原理推导

设$X_1,X_2,...X_M$为训练样本，每个为$N$维。寻找一个$❓\times N$维的矩阵$A$，使$Y=A(X-\overline{X})$，将$X$的维度由$N$降到❓维，❓是自己设定的维度，其值要小于$M$。
PCA要求：
①$A=\left(\begin{array}{c}{a}_1\\ a_2\\ ...\\ a_M\end{array}\right)$，其中$a_i$为$1\times N$维。
②$a_i{a_j}^T=\{\begin{array}{rcl}0& & i\ne j\\ 1& & i=j\end{array}$，即满足正交性。
③方差最大。寻找$a_1$，使${\sum }_{i=1}^p||a_1(x_i-\overline{x})|{|}^2$最大。即$maxmize$${\sum }_{i=1}^p||a_1(x_i-\overline{x})|{|}^2$，下面讨论如何最大化目标函数${\sum }_{i=1}^p||a_1(x_i-\overline{x})|{|}^2$。

函数求解

Ⅰ、$a_1$求解
${\sum }_{i=1}^p||a_1(x_i-\overline{x})|{|}^2=\sum _{i=1}^p{a}_1(x_i-\overline{x}){(x_i-\overline{x})}^T{a}_1^T=a_1\sum a_1^T$，其中$\sum ={\sum }_{i=1}^p(x_i-\overline{x})(x_i-\overline{x}{)}^T$为协方差矩阵，其中约束条件为$a_1{a_1}^T=1$，因此我们采用拉格朗日乘数法。构造如下：
$$object=\{\begin{array}{rlrlrlr}E(a_1)& =& a_1\sum a_1^T-\lambda (a_1{a_1}^T-1)& =& minvalue& & ①\\ \frac{\partial E}{\partial a_1}& =& \sum a_1^T-{\lambda a_1}^T& =& 0& & ②\\ \frac{\partial E}{\partial a_1^T}& =& \sum a_1-\lambda a_1& =& 0& & ③\\ \frac{\partial E}{\partial \lambda }& =& 1-a_1{a}_1^T& =& 0& & ④\end{array}$$
易知④成立，由①$$\frac{\partial E}{\partial a_1}=\sum a_1^T-{\lambda a_1}^T=0$$可得$$\sum a_1^T=\lambda a_1^T$$即有$$a_1\sum a_1^T=a_1(\lambda a_1^T)=\lambda a_1{a}_1^T=\lambda$$因此，$\lambda$为最大的特征值，$a_1^T$为最大特征值对应的特征向量。

Ⅰ、$a_2$求解
与$a_1$求解不同的是$a_2$求解具有两个约束条件：$a_2{a_2}^T=1$、$a_2{a_1}^T=0$
构造如下：
$$object=\{\begin{array}{rlrlrlr}E(a_2)& =& a_2\sum a_2^T-\lambda (a_2{a_2}^T-1)-\beta a_2{a}_1^T& =& minvalue& & ①\\ \frac{\partial E}{\partial a_2}& =& \sum a_2^T-{\lambda a_2}^T-\beta a_1^T& =& 0& & ②\\ \frac{\partial E}{\partial a_2^T}& =& \sum a_2-\lambda a_2& =& 0& & ③\\ \frac{\partial E}{\partial a_1^T}& =& -\beta a_2& =& 0& & ④\\ \frac{\partial E}{\partial \lambda }& =& 1-a_2{a}_2^T& =& 0& & ⑤\\ \frac{\partial E}{\partial \beta }& =& -a_2{a}_1^T& =& 0& & ⑥\end{array}$$
易知⑤，⑥成立，由④$$\frac{\partial E}{\partial a_1^T}=-\beta a_2=0$$又$a_2$为矩阵A的一个向量，A为满秩矩阵，因此$a_2$明显不为零，所以$\beta =0$。又由③$$\frac{\partial E}{\partial a_2^T}=\sum a_2-\lambda a_2=0$$可推出$\lambda$为$\sum$的第二大特征值，$a_2^T$为第二大特征值对应的特征向量。

Ⅰ、$a_i$求解
由上述两种方式，我们可以以此解得，$a_i$为$\sum$的第$i$大特征值，$a_i^T$为第$i$大特征值对应的特征向量。因此我们可知矩阵A是由协方差矩阵$\sum$的特征向量组成，其所包含的特征向量的个数极为我们所需要降到的维度值。

PCA 算法流程

一、对于输入的$N$维向量$X_1、X_2、X_3...、X_p$，求协方差矩阵$$\sum =\sum _{i=1}^p(x_i-\overline{x}){(x_i-\overline{x})}^T$$
二、求$\sum$的特征值和特征向量，按照从特征值从大到小分别是（我们假定所降至维度为$M$维）$${\lambda }_1、{\lambda }_2、{\lambda }_3...、{\lambda }_M、$$由于协方差矩阵是半正定矩阵，它的特征值都是非负的，因此它们对应的特征向量分别为$$a_1^T、a_2^T、a_3^T...、a_M^T$$
三、设$A=\left(\begin{array}{c}{a}_1\\ a_2\\ ...\\ a_M\end{array}\right)$，它是一个$M\times N$维矩阵。$Y_i=A(X_i-\overline{X})$，即$\overline{X}=\frac{1}{p}{\sum }_{i=1}^p{X}_i$，这样即将$N$维向量$X_i$变为$M$维向量$Y_i(M<N)$
附：
①在周志华主编的机器学习书中对PCA算法流程描述如下：

②降维后是不能知晓降维后的数据与原始数据之间的关系，并且有一定的数据损失，因此定义了主成分的贡献率，定义式如下：
$$\{\begin{array}{rlr}\frac{{\lambda }_k}{\sum _{i=1}^n{\lambda }_i}& & 第k个主成分的贡献率\\ & & \\ \frac{\sum _{i=1}^r{\lambda }_i}{\sum _{i=1}^n{\lambda }_i}& & 前r个主成分的贡献率\end{array}$$

PCA matlab计算

本次对单个矩阵得PCA计算采用版本为MATLABR2019b(9.7.01190202)，MATLAB对于矩阵中向量的排列规则是，一行代表一个成员，每一行内的值则是成员的值。在所给出的代码文件中，不仅用MATLAB自带的函数写了PCA算法，还严格按照PCA的算法流程用基本MATLAB语法完成PCA算法，两者输出的值是相同的。MATLAB代码如下：

%% PCA matrix calculate 5 members 2 features
clear; clc;
disp('INFO:Matrix X has 5 members, each of them has 2 features.')
X = sym([-2, -1;0, -1;0, 0;1, 2;1, 0], 'f');
[member, ~]=size(X);
disp('matrix X value:')
disp(X)

% calculate cov(X) by normal method
disp('Calculate cov(X) by normal method.')
mean_value = mean(X, 1);
for i = 1:length(mean(X, 1))
    X(:, i) = X(:, i) - mean_value(i);
end
cov_normal = X' * X / (member - 1);
disp('matrix cov_normal value:')
disp(cov_normal)

% calculate cov(X) by cov function
disp('Calculate cov(X) by cov function.')
cov_function = cov(X);
disp('matrix cov_function value:')
disp(cov_function)

% vector and lamda
[vector, lamda] = eig(cov(X));
total = sum(diag(lamda));
disp('vector and  lamda matrix value:')
disp(vector)
disp(lamda)

% reduction dim
maximum = max(max(lamda));
[index,~]=find(lamda==maximum);
A = vector(:,index);
result = X * A;
disp('final result:')
disp(result)

disp('Energy ratio maximum / total')
disp(maximum / total)


%% PCA matrix calculate 2 members 5 features
clear; clc;
disp('INFO:Matrix X has 2 members, each of them has 5 features.')
X = sym([-2,0,0,1,1;-1,-1,0,2,0], 'f');
[member, ~]=size(X);
disp('matrix X value:')
disp(X)

% calculate cov(X) by normal method
disp('Calculate cov(X) by normal method.')
mean_value = mean(X, 1);
for i = 1:length(mean(X, 1))
    X(:, i) = X(:, i) - mean_value(i);
end
cov_normal = X' * X / (member - 1);
disp('matrix cov_normal value:')
disp(cov_normal)

% calculate cov(X) by cov function
disp('Calculate cov(X) by cov function.')
cov_function = cov(X);
disp('matrix cov_function value:')
disp(cov_function)

% vector and lamda
[vector, lamda] = eig(cov(X));
disp('vector and  lamda matrix value:')
disp(vector)
disp(lamda)

% reduction dim
maximum = max(max(lamda));
[index,~]=find(lamda==maximum);
A = vector(:,index);
result = X * A;
disp('final result:')
disp(result)


%% 3 members 2 features
clear; clc;
disp('INFO:Matrix X has 3 members, each of them has 2 features.')
X = sym([1, 4;2, 5;3, 6], 'f');
[member, ~]=size(X);
disp('matrix X value:')
disp(X)

% calculate cov(X) by normal method
disp('Calculate cov(X) by normal method.')
mean_value = mean(X, 1);
for i = 1:length(mean(X, 1))
    X(:, i) = X(:, i) - mean_value(i);
end
cov_normal = X' * X / (member - 1);
disp('matrix cov_normal value:')
disp(cov_normal)

% calculate cov(X) by cov function
disp('Calculate cov(X) by cov function.')
cov_function = cov(X);
disp('matrix cov_function value:')
disp(cov_function)

% vector and lamda
[vector, lamda] = eig(cov(X));
disp('vector and  lamda matrix value:')
disp(vector)
disp(lamda)

% reduction dim
maximum = max(max(lamda));
[index,~]=find(lamda==maximum);
A = vector(:,index);
result = X * A;
disp('final result:')
disp(result)

在此版本中可以将MATLAB代码转换成实时运行脚本文件，并且可以观察打印输出，具体的输出可自行运行代码文件。截图如下：

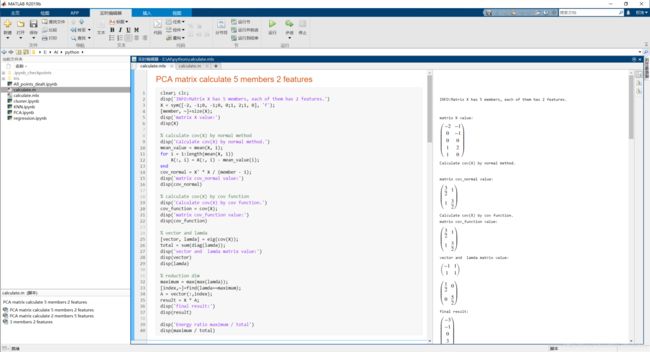
PCA 实现鸢尾花分类

PCA 数据降维处理

导入必要的包

import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
from factor_analyzer import FactorAnalyzer
import matplotlib.pyplot as plt

数据处理

def datafram_dealt(data):
    df_data = pd.read_csv(data)
    df = df_data.drop(['Unnamed: 0'], axis=1)
    class_name = list(df['Species'].drop_duplicates())
    df['Species'] = df['Species'].map({class_name[0]:0, class_name[1]:1, class_name[2]:2}).astype(int)
    df = df.sample(frac=1)
    dick_map = {class_name[0]:0, class_name[1]:1, class_name[2]:2}
    
    return df, dick_map

df, dick_map = datafram_dealt('Iris/iris.csv')

df

	Sepal.Length	Sepal.Width	Petal.Length	Petal.Width	Species
108	6.7	2.5	5.8	1.8	2
93	5.0	2.3	3.3	1.0	1
5	5.4	3.9	1.7	0.4	0
33	5.5	4.2	1.4	0.2	0
95	5.7	3.0	4.2	1.2	1
...	...	...	...	...	...
109	7.2	3.6	6.1	2.5	2
9	4.9	3.1	1.5	0.1	0
4	5.0	3.6	1.4	0.2	0
86	6.7	3.1	4.7	1.5	1
35	5.0	3.2	1.2	0.2	0

150 rows × 5 columns

dick_map

{'setosa': 0, 'versicolor': 1, 'virginica': 2}

获取训练集

train_x = df.iloc[0:120, 0:4]
train_y = df.iloc[0:120, 4]

降维为四个维度，以便查看原始维度中贡献最大的成分，可以发现四个维度贡献分别为0.92011969, 0.05660178, 0.01812305, 0.00515547

model = PCA(n_components=4)

model.fit(train_x)

PCA(copy=True, iterated_power='auto', n_components=4, random_state=None,
    svd_solver='auto', tol=0.0, whiten=False)

model.explained_variance_ratio_

array([0.92096378, 0.05528745, 0.01805879, 0.00568998])

降维为三个维度，在三维坐标系绘图可视化

model = PCA(n_components=3)
model.fit(train_x)
model.explained_variance_ratio_, model.explained_variance_

(array([0.92096378, 0.05528745, 0.01805879]),
 array([4.13008788, 0.24793812, 0.08098514]))

train_x_2D = model.transform(train_x)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(train_x_2D[:, 0], train_x_2D[:, 1], train_x_2D[:, 2], c=train_y)
plt.show()

降维为两个维度，在二维坐标系可视化

model = PCA(n_components=2)
model.fit(train_x)
model.explained_variance_ratio_, model.explained_variance_

(array([0.92096378, 0.05528745]), array([4.13008788, 0.24793812]))

train_x_2D = model.transform(train_x)

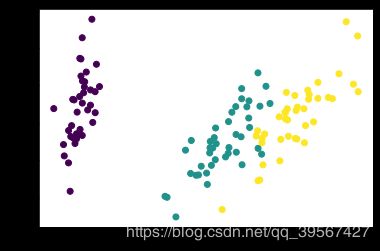
plt.scatter(train_x_2D[:, 0], train_x_2D[:, 1], c=train_y)
plt.show()

自定义保留95％成分，计算机自动计算保留维度，从前面四个维度不难看出，两个维度则占比超过95％，与预期结果相符合

model = PCA(n_components=0.95)
model.fit(train_x)
model.explained_variance_ratio_, model.n_components_

(array([0.92096378, 0.05528745]), 2)

利用mle参数让计算机自动计算保留的维度，结果为三个维度，其成分保留约为99.5％

model = PCA(n_components='mle')
model.fit(train_x)
model.explained_variance_ratio_, model.n_components_

(array([0.92096378, 0.05528745, 0.01805879]), 3)

sum(model.explained_variance_ratio_)

0.9943100204228477

利用因子分析实现组间方差极大化，将数据分隔更开，以三维为例

model = FactorAnalyzer(n_factors=3, rotation='promax')
model.fit(train_x)
model.loadings_

array([[ 1.06466005,  0.07180062, -0.08841903],
       [ 0.00898918,  0.77820767,  0.03874046],
       [ 0.70969381, -0.19615596,  0.26522617],
       [ 0.50775203,  0.0731516 ,  0.63305601]])

train_x_2D = model.transform(train_x)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(train_x_2D[:, 0], train_x_2D[:, 1], train_x_2D[:, 2], c=train_y)
plt.show()

利用因子分析实现组间方差极大化，将数据分隔更开，以二维为例

model = FactorAnalyzer(n_factors=2, rotation='promax')
model.fit(train_x)
model.loadings_

array([[ 0.93854453,  0.16348874],
       [ 0.0110667 ,  1.00086531],
       [ 0.95945583, -0.12708808],
       [ 0.92380573, -0.07361529]])

train_x_2D = model.transform(train_x)

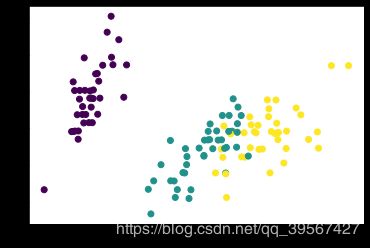
plt.scatter(train_x_2D[:, 0], train_x_2D[:, 1], c=train_y)
plt.show()

KNN实现分类效果

导入必要的包

from sklearn import neighbors

模型建立，利用上一步中最后处理完成的二维数据

model_KNN = neighbors.KNeighborsClassifier()

model_KNN.fit(train_x_2D, train_y)

KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
                     metric_params=None, n_jobs=None, n_neighbors=5, p=2,
                     weights='uniform')

test_x = model.transform(df.iloc[120:150, 0:4])

test_p = model_KNN.predict(test_x)
test_y = df.iloc[120:150, 4].values

print('predict value:', test_p,
      '\nlabel value  :', test_y)

predict value: [1 0 0 1 2 0 1 2 1 0 2 0 1 2 0 1 1 0 2 2 1 0 0 1 1 2 0 0 1 0] 
label value  : [1 0 0 1 2 0 2 2 2 0 2 0 1 2 0 1 1 0 2 1 2 0 0 1 2 2 0 0 1 0]

查看准确率

model_KNN.score(test_x, test_y)

0.8333333333333334

总结

PCA算法能够降低维度，减少数据，其作用与卷积操作类似。最后将处理完成的数据用于神经网路以及传统机器学习算法例如KNN等，都能取得较好的效果