CL关于ORB_SLAM的那些事（PnPsolver）

PnPsolver部分的学习总结

之前看的代码基本都是整个部分的功能，今天开始看一些求解器的cpp，主要就是两个吧，PnPsolver还有Sim3Solver。
，开始吧！

.h部分的浏览

包含的头文件有，opencv、MapPoint.h、Frame.h
PnPsolver类维护的变量（都是私有的）：
double uc, vc, fu, fv：内参？
double * pws, * us, * alphas, * pcs：4个double的指针
int的匹配最大数量
double的两个二维数组（4行3列）
double的行列式值
存放MapPoint的容器
存放二维点的容器
存放Sigma2的float容器
存放三维点的容器
存放关键点在帧内索引的容器
double 3行3列的旋转矩阵
double 3行的平移向量
Mat 第i个变换矩阵
存放是否是内点的标志位的容器
int 内点的数量
int 迭代的次数
存放是否是best内点标志位的容器
int best的内点数量
Mat best变换矩阵
Mat 精制的变换矩阵
存放精制之后是否是内点的标志位容器
int 精制之后内点的数量
int 匹配上的点对的数量
存放随机选择的关键点的索引容器
double RANSAC的概率
Ransac最小的内点数
Ransac最大的迭代次数
Ransac被期望的内点数和总数的比例
Ransac的阈值
Ransac最小集
存放float的最大误差

PnPsolver类中的函数方法：
public:
构造函数
析构函数
设置Ransac参数的函数
find函数
迭代函数
private：
校核内点函数
精制函数
设置最大匹配数量函数
重置匹配函数
添加匹配关系函数
计算位姿函数
相对误差函数
打印位姿函数
重投影误差函数
选择控制点函数
计算重心坐标函数
填充M矩阵函数
计算ccs函数
计算pcs函数
sign的求解器函数
找到find_betas_approx_1函数
找到find_betas_approx_2函数
找到find_betas_approx_3函数
qr求解器函数
两个数的点乘函数
计算距离的平方函数
compute_rho()计算不知道啥的函数
compute_L_6x10()计算啥的函数
高斯牛顿计算函数
计算A和b高斯牛顿的函数
计算旋转和平移矩阵
拷贝旋转和平移矩阵
将Mat转四元数的函数

function by function

cpp文件中包含的除了自身的头文件还有opencv的基本头文件和词袋的头文件
构造函数
PnPsolver()
函数的参数列表：常数帧、常数的存放MapPoint指针的容器
列表初始化：pws(0), us(0), alphas(0), pcs(0), 最大的匹配数量为0, 匹配上的数量为0,最小的内点数为0，迭代次数为0,最好的内点数为0, N(0)
MapPoint的匹配关系被赋值传入的MapPoint指针的容器
维护变量中存放2D、Sigma平方、3D点、关键点索引和所有的索引的容器的大小都是传入帧内MapPoint的数量
定义int索引，初始化为0
循环遍历匹配的MapPoint，取其中的MapPoint，在是MapPoint且不是bad的情况下，取其对应的关键点，获取对应的2D点坐标、该点对应的Sigma平方、该点的3D坐标、关键点的索引和这个点在所有索引的索引值，定义的索引值++
获取该帧相机的标定参数，赋值给fu = F.fx;fv = F.fy;uc = F.cx;vc = F.cy;
最后调用Ransac的参数

析构函数
~PnPsolver()
直接delete [] pws;
delete [] us;
delete [] alphas;
delete [] pcs;

设置Ransac参数的函数
SetRansacParameters()
函数的参数列表：double的概率、内点的数量、最大的迭代的次数、最小的设置、epsilon值和阈值
将传入的概率赋值给Ransac的概率变量
将传入的最小内点数量赋值给Ransac的最小内点数
将传入的最大迭代次数赋值给Ransac的最大迭代次数
将传入epsilon值赋值给Ransac的epsilon变量
将最小的设置值赋值给Ransac的最小设置值
获取2D关键点的数量N
设置存放内点的容器的大小为N
######根据关键点的数量调整参数#############
定义了最小内点数，初始化为N×epsilon
如果定义的这个值小于Ransac的最小内点数，将定义的值赋值为Ransac的最小内点数。
如果定义的这个值小于最小设置值，将定义的值赋值为最小设置值
将定义的最小内点数赋值给Ransac的最小内点数。
如果Ransac的epsilon值小于Ransac的最小内点数/N，就将Ransac的epsilon的值赋值为Ransac的最小内点数/N
定义迭代次数
如果Ransac的最小内点数等于N，迭代次数为1；如果不是，迭代次数为取log(1-Ransac的概率)/log(1-Ransac的3次方)的ceil
给Ransac最大迭代次数赋值为max(1,min(nIterations,mRansacMaxIts))
设置存放最大误差的容器的大小为存放Sigma平方容器的大小
循环赋值最大误差值，最误差值为Sigma的平方*传入的阈值

寻找函数
find()
函数的参数列表：存放bool的内点容器和内点的数量
定义bool的标志位
return 迭代函数的值iterate()

迭代函数
iterate()
函数的参数列表：迭代的次数、不再多的标志位、存放bool类型标志位的内点容器和内点的数量
不再多的标志位置false
清空内点标志位的容器
内点的数量为0
调用set_maximum_number_of_correspondences()函数，设置最大的匹配数量
如果关键点的数量小于Ransac最小的内点数量，将不再多的标志位置true，直接返回空Mat
定义可获取的索引的容器
定义当前迭代的次数为0
当迭代的次数小于Ransac的最大迭代次数或者当前迭代的次数小于迭代次数，一直while循环，当前迭代次数++，总的迭代次数++，调用重置匹配数量函数reset_correspondences()，将所有索引的容器赋值给可获得的索引值容器，循环Ransac的最小设置值，随机产生一个int值，在可获取的索引容器内获取对应位置的索引值，调用添加联系的函数add_correspondence()，用容器的最后一个索引覆盖被抽到的那个索引，最后将最后一个索引pop。通过这个循环获取一个Ransac的点集。调用计算位姿的函数 compute_pose()，调用校核内点的函数CheckInliers()，如果内点的数量不少于Ransac的最小内点数，如果内点的数量大于最好的内点数量，将内点的数量赋值给最好的内点数量，计算得到的旋转和平移矩阵，转换成变换矩阵，判断精制Redine()函数的返回值，如果是true，就把精制的内点数量赋值给内点数，定义存放bool标志位的容器（大小为匹配上的MapPoint的数量，初始化为false）给内点的容器。循环遍历关键点，如果在精制内点的容器内有索引，就在内点容器的该索引处置true，返回精制后的变换矩阵。结束while循环
如果迭代的次数不小于Ransac的最大迭代次数，不再多的标志位置true，如果最好的内点数不小于Ransac的最小内点数，内点数被赋值最好的内点数，同样也定义存放bool标志位的容器（大小为匹配上的MapPoint的数量，初始化为false）给内点的容器，如果在最好内点的容器内有索引，就在内点容器的该索引处置true，返回最好的变换矩阵。
返回空的Mat矩阵。

精制函数
Refine()
定义存放int类型的索引容器，容器的大小为最好内点的数量
循环遍历存放最好内点的容器，将好的内点索引存入刚刚定义的容器内
调用设置最大的联系点数量的函数set_maximum_number_of_correspondences()传入参数索引点的数量
调用重置联系的函数reset_correspondences()
循环遍历索引值的容器，获取索引值，取该索引位置的三维点坐标和二维点坐标，传入add_correspondence()函数
调用计算相机位姿的函数compute_pose()
校核内点的数量CheckInliers()
将内点的数量赋值给精制过的内点数量
将vb的内点数量赋值给精制过的vb内点数量
如果内点的数量大于Ransac的最小内点数量，取出计算出的相机的位姿，转换成变换矩阵赋值给精制的变换矩阵，返回true。
return false

校核内点数
CheckInliers()
将内点的数量初始化为0
循环遍历关键点，获取对应的三维点坐标和二维点的坐标
通过旋转和平移矩阵将三维坐标转换到相机坐标系下
再将相机坐标系下的坐标转换成像素坐标
计算u、v方向的误差
计算像素坐标系下的距离平方
如果距离误差小于最大的误差，将vb内点容器的对应位置置true，内点数++；如果不是，vb内点容器的对应位置置false

设置最大联系点数量
set_maximum_number_of_correspondences()
函数的参数列表：int型的整数
如果传入的要设置最大联系点的数量大于原本的值，对于非零的pws，us，alphas，pcs直接delete
将最大联系点的数量赋值为出传入的值
重新给这个四个数组分配内存

重置联系点数量
reset_correspondences()
将联系点的数量初始化为0

添加联系关系
add_correspondence()
函数的参数列表：三维坐标的x、y、z和二维坐标的u、v
将三维坐标存入pws的数组内
将二维坐标存入us的数组内
联系点的数量++

选择控制的点
choose_control_points()
将cws数据的第一行的1到3列赋值为0
循环遍历联系点的数量，取出三维坐标存入cws的数组中，相当于累加，cws中存入了三维坐标在各个方向上的坐标之和。
对cws数组进行平均值处理
定义创建了联系点数量行、3列float的Mat矩阵
定义了pw0tpw0[3 * 3], dc[3], uct[3 * 3]
定义了其对应的Mat矩阵，3行3列、3行1列、3行3列
循环联系点的数量，获取去均值之后的三维坐标，存入了PW0
调用opencv中的cvMulTransposed函数，将取均值之后的三维坐标，再进行如下操作，

对上面的得到的矩阵进行SVD分解，得到特征值矩阵和U矩阵
调用释放Mat指针的函数，释放PW0的指针
循环3次，取对应的特征值矩阵除上联系点的数量再开平方，得到类似的奇异值，循环遍历均值坐标的三个轴，在原有的基础上再加对应奇异值×U矩阵对应的坐标值，这样做的本质，就是获取在整个大坐标系下的PCA方向。

计算重心坐标
compute_barycentric_coordinates()
定义double的数组cc[3 * 3], cc_inv[3 * 3]
创建3行3列的float的mat矩阵
创建3行3列的float的mat矩阵，这个矩阵是上面矩阵的逆矩阵
循环遍历，得到以均值点作为原点的特征向量的坐标，将这个三个方向组成矩阵
计算得到该矩阵的逆矩阵
定义一个double的指针ci指向这个逆矩阵
循环遍历（联系点的数量），定义行指针，其中再循环三次，计算该逆矩阵乘上去均值之后的三维坐标，alphas的第一列值为1-后面三列的和。经过这样的变换得到由这四个控制点表示的系数。

填充M矩阵
fill_M()
函数的参数列表：Mat的M矩阵、行数、double类型的指针、常量double的u、v值
定义了指向M矩阵的行指针，具体指向哪一行由传入的行参数决定
定义了另一个行指针，该指针永远指向上面那个指针的下一行
循环填补M矩阵中的参数，利用传入的double类型的数组，利用相机内参的反投影u、v方向上的值

计算CCS
compute_ccs()
函数的参数列表：常double的指针betas、常double的指针ut
循环将ccs矩阵中的每个元素置0。ccs为4行3列的矩阵
循环计算在当前坐标系内的４个控制点坐标

计算PCS
compute_pcs()
循环联系点数量次，每次定义两个行指针指向两个矩阵alphas和pcs
下面的一个循环，计算这四个控制点下的３D点在相机坐标系下的坐标，存入pcs矩阵内。

计算位姿
compute_pose()
函数的参数列表：旋转矩阵和平移矩阵
调用选择控制点函数choose_control_points()
调用计算重心坐标函数compute_barycentric_coordinates()
创建M矩阵，2×联系点数量行，12列
循环填充M矩阵，调用填充M矩阵的函数，回过头来看看fill_M()函数就很容易理解了
定义M转置乘M的12行12列的方阵
定义特征值矩阵
定义u转置的特征向量分解矩阵
调用cvMulTransposed()函数，获得M矩阵的转置乘M矩阵的方阵
利用cvSVD()函数分解得到特征值矩阵和特征向量矩阵
释放M矩阵的内存
定义l_6x10[6 * 10], rho[6]矩阵
调用计算l_6x10矩阵的函数compute_L_6x10()，函数的参数传入ut和l_6x10
调用计算rho的函数compute_rho()，函数的参数传入rho
定义double Betas[4][4]，rep_errors[4]，Rs[4][3][3]，ts[4][3]
调用find_betas_approx_1()函数
调用gauss_newton()函数
调用 compute_R_and_t()函数，返回的重投影误差赋值给rep_errors[1]
调用find_betas_approx_2()函数
调用gauss_newton()函数
调用 compute_R_and_t()函数，返回的重投影误差赋值给rep_errors[2]
调用find_betas_approx_3()函数
调用gauss_newton()函数
调用 compute_R_and_t()函数，返回的重投影误差赋值给rep_errors[3]
定义int N并初始化为1
取误差最小的那一组
拷贝计算得到旋转和平移矩阵
最后return该组旋转矩阵和平移矩阵的误差

拷贝旋转和平移矩阵
copy_R_and_t()
函数的参数列表：常double的原始旋转矩阵、常double的原始平移矩阵、拷贝之后的旋转矩阵和拷贝之后的平移矩阵
循环遍历将原始的数据拷贝给拷贝的数据内

计算距离的平方
dist2()
函数的参数列表：两个点的坐标值
直接返回两个点之间距离的平方

点乘
dot()
函数的参数列表：两个向量的首地址
直接返回两个向量点乘的结果

计算重投影误差
reprojection_error()
函数的参数列表：旋转和平移矩阵
定义double的距离的平方sum2变量，初始化为0
循环遍历所有的联系点，取其三维点，然后乘上旋转矩阵，加上平移矩阵，乘上相机的内参矩阵，得到像素坐标，计算与原来像素坐标之间的投影误差，sum2累加误差。
最后返回平均投影误差

估计旋转和平移矩阵
estimate_R_and_t()
函数的参数列表：旋转矩阵和平移矩阵
定义在世界坐标系下的坐标pw0[3]和相机坐标系下的坐标pc0[3]，都初始化为0
循环遍历各个联系点，定义两个行指针指向两个数组的首地址，循环将每个点的坐标进行相加，x、y和z方向的分别累加
循环，计算三个方向的平均值
定义了double abt[3 * 3], abt_d[3], abt_u[3 * 3], abt_v[3 * 3]，第一个矩阵是要分解的矩阵，第二个矩阵是特征值矩阵，第三个是分解出来的u矩阵，最后一个矩阵是分解出来的v矩阵
将这四个矩阵和cvMat的数据结构关联起来
将要分解的矩阵置0
循环构建ABT（看到这边就需要回去看pcs是怎么来的）

对该矩阵进行SVD分解，得到U、V矩阵和特征值矩阵
通过从分解的U、V矩阵中计算获取旋转矩阵
验证该旋转矩阵的行列式是否为1，如果不是就将第三行取反，保证其行列式为正1
将世界坐标系下的坐标乘上旋转矩阵，去除了旋转矩阵的影响，用相机坐标系下的坐标减去刚刚的坐标得到平移矩阵

打印出位姿信息
print_pose()
函数的参数列表：旋转矩阵和平移向量
直接利用cout，标准输入输出把矩阵内的每一个矩阵元素打印出来

解决符号
solve_for_sign()
判断在相机坐标系下的三维点坐标的Z值是否小于０，如果小于０的话，将ccs内的４个控制点取反，将相机坐标系下的三维坐标也取反。

计算旋转和平移矩阵
compute_R_and_t()
函数的参数列表为：SVD之后的Ｕ矩阵，４个控制点的表示系数、旋转矩阵和平移向量
调用compute_ccs(betas, ut)、compute_pcs()函数，得到三维点在相机坐标系下的坐标
调用solve_for_sign()、estimate_R_and_t(R, t)函数，计算得到旋转和平移矩阵
调用reprojection_error(R, t)函数，返回最后这组旋转和平移矩阵计算得到的重投影矩阵

寻找合适的控制点的系数
find_betas_approx_1()
往下涉及到的一些内容需要结合EPnP: An Accurate O(n) Solution to the PnP Problem这篇论文的公式来看一下会更清楚一点。
这个函数是１，后面还有２和３。他们之间的主要区别是选取的系数的数量不一样，所以对应的估计方法也会存在一些差异。
// betas10 　　 = [B11 B12 B22 B13 B23 B33 B14 B24 B34 B44]
// betas_approx_1 = [B11 B12 B13 B14]
当前这个函数取了４个向量，用到的组合是B11 、B12、B13和B14
从Ｌ矩阵内取出对应的元素，组成新的Ｌ矩阵
调用cvSolve()函数，计算得到参数系数。
后面的两个差不多，这边就不进行一一展示了。

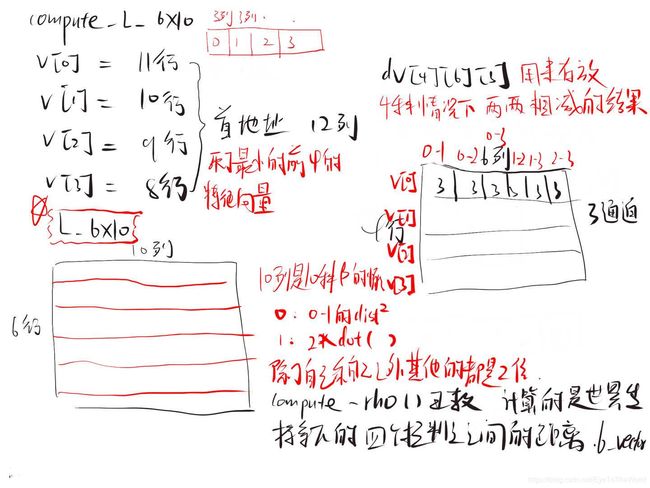
计算Ｌ矩阵
compute_L_6x10()
函数的参数列表：SVD分解出的Ｕ矩阵和Ｌ矩阵
取矩阵的最后四行，因为分解出的奇异向量是按照奇异值从大到小排列的。最后一行是最小的，依次递增。

计算rho矩阵
compute_rho()
函数的参数列表：rho矩阵
计算世界坐标系下的四个控制点两两之间的距离

计算Ａ矩阵和进行高斯牛顿优化
compute_A_and_b_gauss_newton()
函数的参数列表：ｌ矩阵、rho矩阵、４个系数、Ａ矩阵和ｂ矩阵
这边的Ａ矩阵是６个梯度矩阵
ｂ矩阵是世界坐标系下控制点两两之间的距离与对应相机坐标系下的距离之差

高斯牛顿优化
gauss_newton()
函数的参数列表：Ｌ矩阵、Rho矩阵和４个系数
定义迭代的次数为５（根据论文里的描述，进行不到１０次的优化就可以得到好的结果）
往下就是调用compute_A_and_b_gauss_newton()函数，进行两个矩阵的计算
最后调用 qr_solve()函数，计算得到这一次迭代结果
循环将得到的结果累加到４个系数上

QR分解
qr_solve()
函数的参数列表：Ａ矩阵、b矩阵和未知数X矩阵
关于QR分解，我在上一篇博客里有进行学习和总结，这边就不一一赘述。
经过这个函数之后，就能得到变换的系数。

计算相对误差
relative_error()
函数的参数列表：旋转误差、平移误差、真的旋转矩阵、真的平移矩阵、估计的旋转矩阵和估计的平移矩阵
定义真实的四元数和估计的四元数
将真实和估计的旋转矩阵转换成四元数
计算rot_err1：真实和估计之间差值平方和的开方除上真实的四元数的平方和的开方
计算rot_err２：真实和估计之和的平方和的开方除上真实的四元数的平方和的开方
将两个误差比较，取小的那个作为最后旋转的误差
计算平移的误差transl_err：真实和估计之间差值平方和的开方除上真实平移的平方和的开方

将Mat转四元数
mat_to_quat()
函数的参数列表：旋转矩阵和四元数
计算旋转矩阵主元的和，也就是矩阵的迹
定义一个double的变量n4

时间：2019年09月08日
作者：hhuchen
机构：河海大学机电工程学院