2020牛客暑期多校训练营（第二场）J Just Shuffle

2020牛客暑期多校训练营（第二场）J Just Shuffle

题目链接

现学组合数学+置换群，结果还是没ac，补题补题

J Just Shuffle

对于一个排列A，给定一个置换规则P，在使用置换P K 次后得到新的排列B
A ^ K = B
输入：B K
输出：A（如果无解输出-1）
//昨天就被这个题目坑了，我还在想什么情况出现无解，这就是现学的后果（一知半解），后来我才知道题目中表明K是个大质数，说明K一定存在逆元，不会出现无解的情况。
|
|
|
|

置换群概念介绍

那么我们先来了解一下置换群的概念
（引自博主Yoangh原创内容)
链接: https://blog.csdn.net/y990041769/java/article/details/45172095.
首先给你一个序列，假如：
s = {1 2 3 4 5 6}
然后给你一个变换规则
t = {6 3 4 2 1 5}
就是每一次按照t规则变换下去
比如这样
第一次：6 3 4 2 1 5
第二次：5 4 2 3 6 1
第三次：1 2 3 4 5 6
发现经过几次会变换回去，在变换下去就是循环的了，这就是一个置换群。
我们可以这样表示一个置换群，比如按照上面变化规则
1->6->5->1 那么这些是一个轮换
2->3->4->2 这些是一个轮换
所以可以写为
t = { {1 6 5},{ 2 3 4 } }
|
|
|
|

解题

回到该题
A ^ K = B
且P等于A再置换一次
我们设Z为K的逆元，r为置换循环节，则 B ^ Z = A
//逆元定义如下：

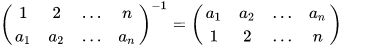
Z * K % r == 0 ，(r为置换循环节)
令Z：Z * K % r == 1
求出Z，然后让B置换Z次即可得A。
补充解析：

代码

#include 
#include 
#include 
using namespace std;
typedef long long ll;
const double PI = 3.141593;
const int N = 1e5 + 1;
int a[N], b[N], c[N];
vector <int > v;

void solve(int k)
{
	int i, j;
	int r = v.size(), inv;
	for(i = 0; i < r; i ++)
		if((ll)k * i % r == 1)
			inv = i;
	for(j = 0; j < r; j ++)
		c[v[j]] = v[(j + inv) % r];
}

int main()
{
	int n, k;
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>n>>k;
	for(int i = 1; i <= n; i ++)
		cin>>b[i];
	for(int i = 1; i <= n; i ++)
	{
		if(!a[i])
		{
			v.clear();
			int x = b[i];
			while(!a[x])
			{
				a[x] = 1;
				v.push_back(x);
				x = b[x];
			}
			solve(k);
		}
	}

	for(int i = 1; i <= n; i ++)
	{
		if(i != n)
			cout<<c[i]<<" ";
		else
			cout<<c[i]<<endl;
	}
	return 0;
}