视觉slam14讲学习（五）之视觉里程计组成:特征点法

1. 特征点提取和匹配

以orb特征为例,步骤1初始化:

 //-- 读取图像
    Mat img_1 = imread ( argv[1], CV_LOAD_IMAGE_COLOR );
    Mat img_2 = imread ( argv[2], CV_LOAD_IMAGE_COLOR );

    //-- 初始化
    std::vector keypoints_1, keypoints_2;
    Mat descriptors_1, descriptors_2;
    Ptr detector = ORB::create();
    Ptr descriptor = ORB::create();
    // Ptr detector = FeatureDetector::create(detector_name);
    // Ptr descriptor = DescriptorExtractor::create(descriptor_name);
    Ptr matcher  = DescriptorMatcher::create ( "BruteForce-Hamming" );

步骤2检测两幅图像的角点

  //-- 第一步:检测 Oriented FAST 角点位置
    detector->detect ( img_1,keypoints_1 );
    detector->detect ( img_2,keypoints_2 );

步骤3计算各个特征点的相似度

    //-- 第二步:根据角点位置计算 BRIEF 描述子
    descriptor->compute ( img_1, keypoints_1, descriptors_1 );
    descriptor->compute ( img_2, keypoints_2, descriptors_2 );

    Mat outimg1;
    drawKeypoints( img_1, keypoints_1, outimg1, Scalar::all(-1), DrawMatchesFlags::DEFAULT );
    imshow("ORB特征点",outimg1);

步骤4进行匹配

    //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
    vector matches;
    //BFMatcher matcher ( NORM_HAMMING );
    matcher->match ( descriptors_1, descriptors_2, matches );

步骤5进行筛选

    //-- 第四步:匹配点对筛选
    double min_dist=10000, max_dist=0;

    //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        double dist = matches[i].distance;
        if ( dist < min_dist ) min_dist = dist;
        if ( dist > max_dist ) max_dist = dist;
    }
    
    // 仅供娱乐的写法
    min_dist = min_element( matches.begin(), matches.end(), [](const DMatch& m1, const DMatch& m2) {return m1.distancedistance;
    max_dist = max_element( matches.begin(), matches.end(), [](const DMatch& m1, const DMatch& m2) {return m1.distancedistance;

    printf ( "-- Max dist : %f \n", max_dist );
    printf ( "-- Min dist : %f \n", min_dist );

    //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
    std::vector< DMatch > good_matches;
    for ( int i = 0; i < descriptors_1.rows; i++ )
    {
        if ( matches[i].distance <= max ( 2*min_dist, 30.0 ) )
        {
            good_matches.push_back ( matches[i] );
        }
    }

步骤6绘图

    //-- 第五步:绘制匹配结果
    Mat img_match;
    Mat img_goodmatch;
    drawMatches ( img_1, keypoints_1, img_2, keypoints_2, matches, img_match );
    drawMatches ( img_1, keypoints_1, img_2, keypoints_2, good_matches, img_goodmatch );
    imshow ( "所有匹配点对", img_match );
    imshow ( "优化后匹配点对", img_goodmatch );
    waitKey(0);

结果显示:

2. 2d-2d对极几何

(单目相机)在只知道2d的像素信息的情况下,估计相机位置需要使用2d-2d对极几何的原理.

2.1 对极几何原理

基本概念:

1. 基线（baseline）：O1O2为基线
2. 极平面（epipolar plane）：任何包含基线的平面都称为对极平面，或者说是对极平面束中的平面
3. 极点（epipole）：摄像机的基线与每幅图像的交点；即上图中的点el和er
4. 极线（epipolar line）：对极平面与图像的交线；例如，上图中的直线ep

对应点的约束
现在假设只知道图像点x，那么，它的对应点x’如何约束呢？

根据前面的讨论，点x和x’一定位于平面π上，而平面π可以利用基线和图像点x的反投影射线确定;
且点x的对应点x’一定位于它的极线上！

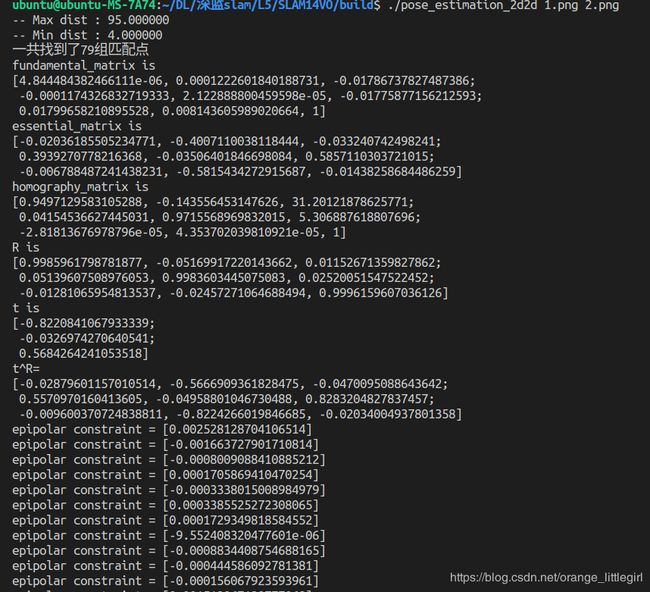
2.2 基本矩阵F和本质矩阵E

两幅图像中的像素点p1,p2对应的归一化平面的坐标分别为x1和x2
由一次旋转和平移和进行坐标转化:
$x_1=K^{-1}{p}_1$; $x_2=K^{-1}{p}_2$
$x_2=R{x}_1+t$
两边同时左乘t^, 再做乘$x_2^T$,t^t=0得:
$x_2^T$t^$x_2$ =$x_2^T$t^R$x_1$
左边容易证得为0,所以有:
$x_2^T$t^R$x_1$=0
代入p1和p2,得到:
$p_2^T{K}^{-T}$t^R$K^{-1}{p}_1$=0
该式子是对极约束的代数表达,几何意义是O1,O2,P三点共面
令E={t^}R为本质矩阵
令$F=K^{-T}$E $K^{-1}$为基本矩阵
注意t^是平移向量对应的反对称矩阵
$t^{=}[0,-z,y;z,0,-x;-y,x,0]$

2.3 2d-2d位姿估计

• 问题求解:
  1.根据配对点像素点位置求解E或者F
  2.根据E,F求解R,t

• 一般用8点法求E,接下来介绍其原理
  由对极约束$x_2^T$$E$$x_1=0$, $E$为3x3矩阵, $x_1=(u_1,v_1,1{)}^T$, $x_2=(u_2,v_2,1{)}^T$,得
  $(u_1,v_1,1)$$(e_1,e_2,e_3;e_4,e_5,e_6;e_7,e_8,e_9)$$(u_2,v_2,1{)}^T$=0
  由于KE=0,所以$E$有9-1=8个自由度,求解E的时候,解不唯一(有无数解,kx)
  得线性方程组:
  $(u_1{u}_2,u_1{v}_2,u_1,v_1{u}_2,v_1{v}_2,v_1,u_2,v_2,1)e=0$
  所以8对点才能求解
  $e=(e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9{)}^T$
  设E的奇异值分解为:
  $E=U\Sigma V^T$

• 从E恢复R和t
  通过奇异值分解求解:
  
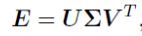
  有四个解分别$t_1{R}_1,t_2{R}_2,t_2{R}_1,t_2{R}_2$为:
  
  
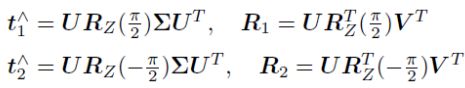
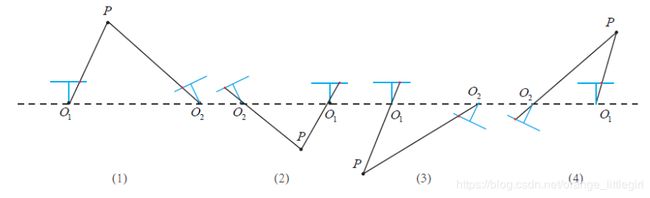
  图解:
  (1), (3)表示$O_1到O_2$, 且像素点不能发生变化, 只能将$O_2$点处相机位置旋转-90度
  (2), (4)表示$O_2到O_1$, 且像素点不能发生变化, 只能将$O_2$点处相机位置旋转-90度
  注意, 只有(1)情况下, P点在两个相机处具有正深度, 同样可以通过测试深度的正负来判断属于哪种情况

• 八点法注意的问题:
  用于单目SLAM的初始化
  尺度不确定性：归一化 t 或特征点的平均深度
  纯旋转问题：t=0 时无法求解
  多于八对点时：最小二乘
  有外点时：RANSAC

• 利用5点法求解R,t
  

• 利用单应矩阵H求解R,t
  原理:
  
  注意: 通常会同时利用E和H估计位姿,最后取重投影误差小的为最优位姿估计.

• 代码实践:

void pose_estimation_2d2d ( std::vector keypoints_1,
                            std::vector keypoints_2,
                            std::vector< DMatch > matches,
                            Mat& R, Mat& t )
{
    // 相机内参,TUM Freiburg2
    Mat K = ( Mat_ ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );

    //-- 把匹配点转换为vector的形式
    vector points1;
    vector points2;

    for ( int i = 0; i < ( int ) matches.size(); i++ )
    {
        points1.push_back ( keypoints_1[matches[i].queryIdx].pt );
        points2.push_back ( keypoints_2[matches[i].trainIdx].pt );
    }

    //-- 计算基础矩阵
    Mat fundamental_matrix;
    fundamental_matrix = findFundamentalMat ( points1, points2, CV_FM_8POINT );
    cout<<"fundamental_matrix is "<

• 实验效果:
  

2. 3d-2d估计方法