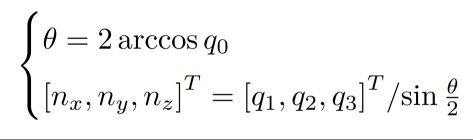【视觉SLAM十四讲】三维空间刚体运动

本文为视觉 SLAM 学习总结。第三讲讲解的是观测方程中的 $x$ 是什么。

本讲内容概要

• 三维空间的刚体运动的描述方式：旋转矩阵、变换矩阵、四元数和欧拉角
• Eigen 库的矩阵、几何模块的使用方法

旋转矩阵

点和向量，坐标系

定义坐标系后，向量可由 $R^3$ 坐标表示：
$$a=[e_1,e_2,e_3]\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right]=a_1{e}_1+a_2{e}_2+a_3{e}_3$$
直接用坐标进行向量间的运算。

我们对外积进行介绍，这个概念在之后的学习中会经常使用，我们可以将向量叉乘写为矩阵点乘的形式：

其中 a^ 表示将向量转换为矩阵的形式，为反对称矩阵，也可称为反对称符号。

坐标系间的欧式变换

SLAM 中有两个坐标系，一个是世界坐标系，通常以地面参考，另一个为机器人坐标系，会随着机器人的运动而运动。

那么坐标系之间是如何变化的？如何计算同一个向量在不同坐标系下的坐标？

直观来看，我们需要用旋转+平移来描述刚体运动。

• 坐标系原点的平移
• 三个轴的旋转。

同一向量在不同坐标系下可以被描述为以下两种不同的形式：

左乘 $\left[\begin{array}{c}{e}_1^T\\ e_2^T\\ e_3^T\end{array}\right]$，得：

将中间的矩阵定义为 $R$，称为旋转矩阵。其性质有：正交矩阵且行列式=1；相反，满足这些性质的矩阵也可以称为旋转矩阵，也称为特殊正交群，定义如下：
$$SO(n)=\{R\in R^{n\times n}|R{R}^T=I,det(R)=1\}$$
当 $n=3$ 时为 $SO(3)$ 的旋转矩阵。

旋转矩阵描述了两个坐标的变换关系。$a_1=R_{12}{a}_2,a_2=R_{21}{a}_1$，于是：
$$R_{21}=R_{12}^{-1}=R_{12}^T$$
进一步，三个坐标系（多次旋转）亦有：
$$a_3=R_{32}{a}_2=R_{32}{R}_{21}{a}_1=R_{31}{a}_1$$
这么多矩阵连乘看起来很复杂？我们可以用一个技巧来记忆：观察下标，我们可以将下标相连的变量进行组合，如：$R_{32}{R}_{21}=R_{31}$。

再加上平移：$a^{{}^{\prime }}=Ra+t$。两个坐标系的刚体运动可完全由 $R,t$ 描述。

变换矩阵与期齐次坐标

但我们连续进行坐标变换时，叠加形式过于复杂：
$$c=R_2(R_{1}a+t_1)+t_2$$
我们需要引入变换矩阵的概念，改变形式：

可以将旋转+平移的计算放在一个矩阵中。$T$ 称为变换矩阵. $a˜$ 表示 $a$ 的齐次坐标，则多次变换可写成：
$$b˜=T_{1}a˜,c˜=T_{2}b˜\Rightarrow c˜=T_2{T}_{1}a˜$$
用 4 个数描述三维向量的做法称为齐次坐标，这里引入齐次坐标是为了让矩阵运算能够符合规则——4×4 的矩阵与 3×1 的矩阵无法相乘，需给 3×1 的矩阵增加一维。

变换矩阵称为特殊欧式群，定义如下：

可定义反向变换矩阵为：

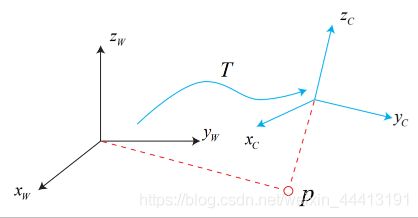
在 SLAM 中，通常定义世界坐标系 $T_W$ 与机器人坐标系 $T_R$。若一个点的世界坐标为 $p_W$，机器人坐标系下为 $p_R$，那么满足关系：
$$p_R=T_{RW}{p}_W$$
反之亦然。在实际编程中，可使用 $T_{RW}$ 或 $T_{WR}$ 来描述机器人的位姿。

当我们给 $T_{RW}$ 乘零向量的齐次坐标后，得到一个平移向量，这个向量是世界坐标系原点在机器人坐标系中的位置；如果是 $T_{WR}$ 则为机器坐标系在世界坐标系下的位置，即为机器人的运动轨迹。

实践部分：EIGEN

EIGEN 效率较高，我们通常用其描述 C++ 中的一些矩阵运算。

我们可以用下面的命令安装 EIGEN：

sudo apt-get install libeigen3-dev

可以输入 ls /usr/include/eigen3 找到 EIGEN 的安装位置。EIGEN 是一个全是头文件的库，没有库文件，因此无需链接库 target_link_libraries()，仅仅把头文件目录加入就可以了。下面为 CMakeLists.txt 的内容：

cmake_minimum_required( VERSION 2.8 )
project( useEigen )

set( CMAKE_BUILD_TYPE "Release" )
set( CMAKE_CXX_FLAGS "-O3" )

# 添加Eigen头文件，一般会先进行搜索，然后再添加。
include_directories( "/usr/include/eigen3" )

# in osx and brew install
# include_directories( /usr/local/Cellar/eigen/3.3.3/include/eigen3 )

add_executable( eigenMatrix eigenMatrix.cpp )

其中 Eigen/Core 提供了一些核心的矩阵运算。

我们可以看到 Matrix 中的模板参数如下，有 6 个参数组成的类，较为复杂。

// _Scalar为类型，_Rows、_Rows分别为行列，固定不变时可以指定大小，后面有默认值
template<typename _Scalar, int _Rows, int _Rows, int _Options, int _MaxRows, int _MaxCols>

若提前已知矩阵大小，可对矩阵进行加速，动态类型较慢。EIGEN 中还有一些内置的小矩阵，如 Matrix3f 为 3×3 的浮点数矩阵，转到其定义可以发现其实就是一个 typedef。如 Vector3d 其实是一个 1×3 的矩阵。

// 矩阵定义后赋初值
Eigen::Matrix3d matrix_33 = Eigen::Matrix3d::Zero();
// 如果不确定矩阵大小，可以使用动态大小的矩阵。转到Dynamic定义：const int Dynamic = -1;
Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > matrix_dynamic;
// 更简单的动态大小的矩阵，X表示不知道维度
Eigen::MatrixXd matrix_x;

下面对 Eigen 阵的操作：

// 流输入符，输入数据（初始化）。类中重载了 <<
matrix_23 << 1, 2, 3, 4, 5, 6;
// 直接cout输出
cout << matrix_23 << endl;
// 用()访问矩阵中的元素，重载了()。
// 对于向量如 Vector3d v_3d，可以写中括号运算符v_3d[0]当作数组。
for (int i=0; i<2; i++) {
	for (int j=0; j<3; j++)
		cout<<matrix_23(i,j)<<"\t";
	cout<<endl;
}

// 矩阵和向量相乘（实际上仍是矩阵和矩阵），重载了乘号
// 但是在Eigen里你不能混合两种不同类型的矩阵，像这样是错的：double不能乘float。
// 此时会报错一长串，很难找到问题。
// 如：Eigen::Matrix result_wrong_type = matrix_23 * v_3d;
// 应该显式转换（c++中有隐式类型提升）
Eigen::Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;

// 同样不能搞错矩阵的维度
// Eigen::Matrix result_wrong_dimension = matrix_23.cast() * v_3d;

下面演示一些矩阵的运算：

// 四则运算就不演示了，直接用+-*/即可。
matrix_33 = Eigen::Matrix3d::Random();      // 随机数矩阵
cout << matrix_33 << endl << endl;
cout << matrix_33.transpose() << endl;      // 转置
cout << matrix_33.sum() << endl;            // 各元素和
cout << matrix_33.trace() << endl;          // 迹，即对角线元素和
cout << 10*matrix_33 << endl;               // 数乘
cout << matrix_33.inverse() << endl;        // 逆，矩阵规模很大时耗时
cout << matrix_33.determinant() << endl;    // 行列式

下面演示如何求解特征值，特征值的概念见《线性代数》：

// 实对称矩阵可以保证对角化成功
Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver ( matrix_33.transpose() * matrix_33 );
cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;

下面演示解方程：

// 我们求解 matrix_NN * x = v_Nd 这个方程
// N的大小在前边的宏里定义，它由随机数生成
// 直接求逆自然是最直接的，但是求逆运算量大
Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
Eigen::Matrix< double, MATRIX_SIZE,  1> v_Nd;
v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );

clock_t time_stt = clock(); // 计时
// 直接求逆
Eigen::Matrix<double,MATRIX_SIZE,1> x = matrix_NN.inverse()*v_Nd;
cout <<"time use in normal inverse is " << 1000* (clock() - time_stt) / (double)CLOCKS_PER_SEC << "ms"<< endl;

// 通常用矩阵分解来求，例如QR分解，速度会快很多
time_stt = clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
cout <<"time use in Qr decomposition is " <<1000*  (clock() - time_stt)/ (double)CLOCKS_PER_SEC <<"ms" << endl;

关于矩阵分解的相关知识见《矩阵论》。

旋转向量与欧拉角

旋转向量

一个三维的旋转最少可以用三个数进行描述，但我们的旋转矩阵使用了 3×3=9 个数字描述，浪费存储空间，不够紧凑。并且旋转矩阵还有一些约束，不能当作普通的矩阵进行优化。因此我们考虑用其他方式进行描述。

我们任意一次旋转可以分解为绕着一个轴 $w$ 转过了一个角度。

方向为旋转轴方向 $n$、长度为转过的角度 $\theta$ 的向量，被称为角轴或旋转向量。角轴只有三个量，且没有约束。角轴也就是 CH4 中要介绍的李代数。
$$w=\theta n$$
角轴与旋转矩阵之间可以相互转换。角轴转旋转矩阵使用罗德里格斯公式（直接给出结果）：

如果我们知道了 $R$，也可以转换为角轴：

• 角度：$\theta =arccos(\frac{tr(R)-1}{2})$
• 轴：$Rn=n$。轴 $n$ 在旋转后不动，因此 $n$ 对应为矩阵 $R$ 特征值为 1 的特征向量，解出方程即可。

欧拉角

旋转矩阵和旋转向量不是很直观，欧拉角是一种直观的表示方法，方便人观察，常用于人机交互，程序中很少用来描述旋转。

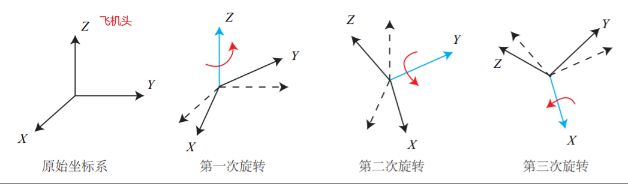
欧拉角将一次旋转分界为三次不同轴上的转动，可以求出绕每个轴转动了多少度。因描述转动的轴的顺序可以不同，且分为转动前的轴（定轴）和转动后的轴（动轴），欧拉角有多种定义方式，常见的为 yaw-pitch-roll（偏航-俯仰-滚转）角。

1. 绕 Z 轴旋转，得到偏航角 yaw；
2. 绕旋转之后的 Y 轴旋转，得到俯仰角 pitch；
3. 绕旋转之后的 Z 轴旋转，得到滚转角 roll。

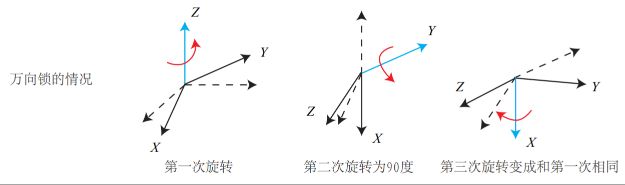
万向锁问题：

下图中第三次旋转和第一次旋转其实是绕着同一个轴进行旋转，使得系统少了一个自由度——存在奇异性问题。

因万向锁的问题，欧拉角很少在 SLAM 中使用，仅与人进行交互。

四元数

（单位圆上）复数可以表达二维平面的旋转。四元数是一种扩展的复数，有 3 个虚部，可以描述三维空间的旋转：
$$q=q_0+q_{1}i+q_{2}j+q_{3}k$$
四元数由一个实部和一个虚部向量组成， $q=[s,v]$，$s=q_0\in R,v=[q_1,q_2,q_3{]}^T\in R^3$。

虚部之间的关系：

记忆技巧：自己和自己运算像复数，自己和别人运算像叉乘。

四元数的运算性质

• 加减法：实部和虚部分别相加
• 乘法：与复数相同
• 共轭 $q^{\ast }$：虚部取反
• 模长：各部分平方开根号
• 逆：$q^{-1}=q^{\ast }/||q|{|}^2$
• 点乘：$q_a\cdot q_b=s_a{s}_b+x_a{x}_{b}i+y_a{y}_{b}j+z_a{z}_{b}k$

四元数与角轴的关系

角轴到四元数：
$$q=[cos\frac{\theta }{2},n_{x}sin\frac{\theta }{2},n_{y}sin\frac{\theta }{2},n_{z}sin\frac{\theta }{2}{]}^T$$
四元数到角轴：

四元数亦可转换为旋转矩阵、欧拉角。

四元数表示旋转

设点 $p$ 经过一次以 $q$ 表示的旋转后，得到了 $p^{\prime }$，它们的关系：

1. 将 $p$ 的坐标用四元数表示（虚四元数）：$p=[0,x,y,z]=[0,v]$
2. 旋转之后的关系：$p^{\prime }=qp{q}^{-1}$，可以验证 $p^{\prime }$ 也是四元数。几何意义是先把四元数转到四维空间中，然后再转回来。

四元数紧凑、无奇异性。

以上这些方法中，最常用的是矩阵和四元数。当把轨迹存到文件中时通常使用四元数，矩阵太麻烦。

实践部分：EIGEN 几何模块

下面程序演示 Eigen 几何模块的使用方法。Eigen/Geometry 模块提供了各种旋转和平移的表示。

3D 旋转矩阵直接使用 Matrix3d 或 Matrix3f：

// 3D 旋转矩阵直接使用 Matrix3d 或 Matrix3f
// 这里为单位矩阵，表示没有旋转
Eigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();

旋转向量使用AngleAxis, 底层不直接是Matrix，但运算可以当作矩阵（因为重载了运算符）：

// 给定沿哪个轴转多少角度，这里沿 Z 轴旋转 45 度
Eigen::AngleAxisd rotation_vector ( M_PI/4, Eigen::Vector3d ( 0,0,1 ) );
cout .precision(3);
// 调用成员函数matrix，将角轴转换为矩阵
cout<<"rotation matrix =\n"<<rotation_vector.matrix() <<endl;
// 也可以直接赋值，使用toRotationMatrix
rotation_matrix = rotation_vector.toRotationMatrix();

可以进行坐标变换：

// 用 AngleAxis 可以进行坐标变换
Eigen::Vector3d v ( 1,0,0 );
Eigen::Vector3d v_rotated = rotation_vector * v; // 重载了*，旋转v
cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
// 或者用旋转矩阵，打印结果相同
v_rotated = rotation_matrix * v;
cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;

得到结果相同：

可以将旋转矩阵直接转换成欧拉角：

Eigen::Vector3d euler_angles = rotation_matrix.eulerAngles ( 2,1,0 ); // ZYX顺序，即roll pitch yaw顺序
cout<<"yaw pitch roll = "<<euler_angles.transpose()<<endl;

欧氏变换矩阵使用 Eigen::Isometry：

// 旋转为0，平移也为0的标准变换矩阵
Eigen::Isometry3d T=Eigen::Isometry3d::Identity(); // 虽然称为3d，实质上是4＊4的矩阵
T.rotate ( rotation_vector ); // 按照rotation_vector进行旋转，将旋转放到变换矩阵中
T.pretranslate ( Eigen::Vector3d ( 1,3,4 ) ); // 把平移向量设成(1,3,4)
cout << "Transform matrix = \n" << T.matrix() <<endl;

用变换矩阵进行坐标变换：

Eigen::Vector3d v_transformed = T*v; // 相当于R*v+t，重载了*自动转换为齐次坐标
cout<<"v tranformed = "<<v_transformed.transpose()<<endl;

四元数：

// 可以直接把AngleAxis赋值给四元数，反之亦然。
Eigen::Quaterniond q = Eigen::Quaterniond ( rotation_vector );
// 请注意coeffs的顺序是(x,y,z,w),w为实部，前三者为虚部！！！
cout<<"quaternion = \n"<<q.coeffs() <<endl;
// 也可以把旋转矩阵赋给它
q = Eigen::Quaterniond ( rotation_matrix );
cout<<"quaternion = \n"<<q.coeffs() <<endl;

//Eigen::Matrix3d qx = q.toRotationMatrix();// 四元数转换为矩阵

// 使用四元数旋转一个向量，使用重载的乘法。
v_rotated = q*v; // 先将向量转换为四元数，数学上是qvq^{-1}
cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;

以上仅演示了基本的做法。更深入的操作可以查看 EIGEN 库文档。