全序与偏序关系
全序与偏序关系
- 集合上的关系问题
- 偏序与全序的概念
- 举例
- 应用
- 总结
集合上的关系问题
假设A是一个集合 {1,2,3} ;R是集合A上的关系,例如{<1,1>,<2,2>,< 3,3>,<1,2>,<1,3>,<2,3>}
自反性:任取一个A中的元素x,如果都有
对称性:任取两个A中的元素x,y,如果
反对称性:任取两个A中元素x,y(x!=y),如果
传递性:任取三个A中元素x,y,z,如果
偏序与全序的概念
偏序: 设R是非空集合A上的关系,如果R是自反的,反对称的,和传递的,则称R是A上的偏序关系。
偏序的定义:设R是集合A上的一个二元关系,若R满足:
Ⅰ 自反性:对任意x∈A,有xRx;
Ⅱ 反对称性(即反对称关系):对任意x,y∈A,若xRy,且yRx,则x=y;
Ⅲ 传递性:对任意x, y,z∈A,若xRy,且yRz,则xRz。 则称R为A上的偏序关系。
全序:如果R是A上的偏序关系,那么对于任意的A集合上的 x,y,都有 x <= y,或者 y <= x,二者必居其一,那么则称R是A上的全序关系。
全序的定义:设集合X上有一全序关系,如果我们把这种关系用 ≤ 表述,则下列陈述对于 X 中的所有 a, b 和 c 成立:
如果 a ≤ b 且 b ≤ a 则 a = b (反对称性)
如果 a ≤ b 且 b ≤ c 则 a ≤ c (传递性) a ≤ b 或 b ≤ a (完全性)
注意:完全性本身也包括了自反性。 所以,全序关系必是偏序关系
所以可以看到,全序也是一种偏序。偏序究竟在说啥,关键在于反对称性上,就是说,
举例
偏序举例:
假设有 A={1,2,3,4},假设R是集合A上的关系:{<1,1>,<2,2>,< 3,3>,<4,4>,<1,2>,<1,4>,<2,4>,< 3,4>},那么:
自反性:可以看到 <1,1>,<2,2>,< 3,3>,<4,4> 都在R中,满足。
反对称性:由于 <1,1>,<2,2>,< 3,3>,<4,4> 不属于 x !=y ,所以不考虑这4种,对于 <1,2>,有 <2,1> 不在R中;对于<2,4> 有<4,2>不在R中;对于<3,4> 有<4,3> 不在 R中,满足。
传递性:<1,1><1,2>在R中,并且<1,2>在R中;<1,1><1,4>在R中,并且<1,4>在R中;<2,2><2,4>在R中,并且<2,4>在R中;< 3,3><3,4>在R中,并且<3,4>在R中;等等其他,满足。所以说R是偏序关系。
全序举例:
假设有 A={a,b,c},假设R是集合A上的关系:{
应用
这个概念有什么用:
在 《Time, Clocks, and the Ordering of Events in a Distributed System》 论文中介绍到,我们一般怎么定义一个事情是在另一个事情之前发生,很简单,看看时间就完事了,在这单机或者说单服务器,单核下是没问题的。
但是,在计算机分布式系统中,假设有A,B两个服务器,他们的本机时间可能不同步的,或者有差别的,或者说不准的,那么这个时候,你就很难定义A服务器的这个请求先发生,还是B服务器的这个请求先发生。所以在论文里面,Lamport 是这样定义的:
(1) If a and b are events in the same process, and a comes before b, then a -> b.
(2) If a is the sending of a message by one process and b is the receipt of the same message by another process, then a -> b.
(3) If a-> b and b-> c then a -> c. Two distinct events a and b are said to be concurrent if a 非-> b and b 非-> a.
那么我们假设没有最后一句会出现什么:
Two distinct events a and b are said to be concurrent if a 非-> b and b 非-> a
如下图所示:
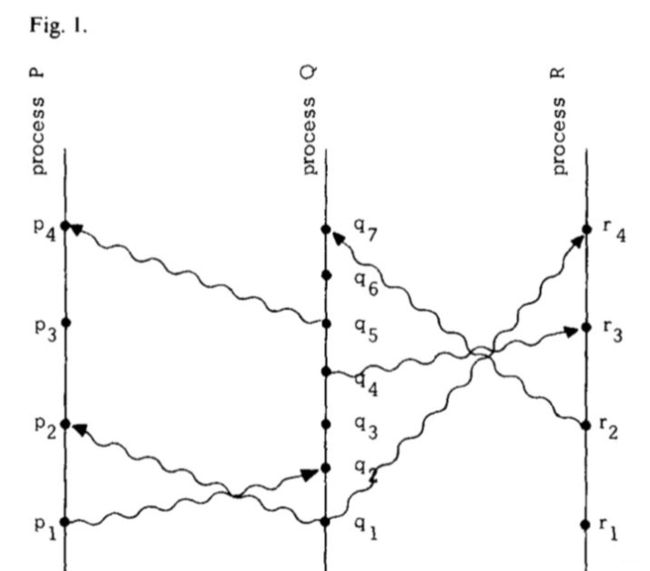
这里我们可以看到 3 个处理器,你可以认为是3个服务器,这个时候,P服务器的 p3处理一个请求,Q服务器q3也处理一个请求,并且这两个请求没有任何关系,那么他们谁先谁后,虽然看起来是q3先,但是P服务器在 p4节点之前根本不知道Q服务器的实际运行q3时间啊,所以这个时候,Lamport 加了一个条件,这种情况下(P服务器在 p4节点之前)这两个事件p3和q3算是并发的。
上面这种算法是怎么实现的呢:其实也不难,对于单核处理器,每一个事件,计数器 i++ 即可。对于不同处理器,有因果关系的,当发送消息的时候,也把自己的这个计数传过去,然后另外一个处理器取 Math.max(currentValue, 传过来的计数) + 1 即可。
那么这样计数就有问题了,A服务器和B服务器的计数有可能在某个物理时刻是相等的呢,相等怎么办,Lamport 给出的定义就是相等我们就看两个服务器的编号比较大小。
总结
通过上面,可以感性的认识到,偏序关系实际上就是你没考虑全了,全序关系就是你需要补上一下关系,让全部情况都适用了。