数学建模 matlab 标准规划问题的MATLAB求解

一、线性规划

1.发展进程
运筹学的一个重要分支是数学规划，而线性规划（Linear Programming，LP）则是数学规划的一个重要分支。

1947年美国数学家G. B. Dantzig（丹齐克）提出线性规划的一般数学模型和求解线性规划问题的通用方法──单纯形法，为这门学科奠定了基础。
1947年美国数学家John von诺伊曼提出对偶理论，开创了线性规划的许多新的研究领域，扩大了它的应用范围和解题能力。
1951年美国经济学家T.C.库普曼斯把线性规划应用到经济领域，为此与康托罗维奇一起获1975年诺贝尔经济学奖。
2.基本概念
问题：央视为改版后的《非常6＋1》栏目播放两套宣传片。其中宣传片甲播映时间为3分30秒，广告时间为30秒，收视观众为60万，宣传片乙播映时间为1分钟，广告时间为1分钟，收视观众为20万。广告公司规定每周至少有3.5分钟广告，而电视台每周只能为该栏目宣传片提供不多于16分钟的节目时间。电视台每周应播映两套宣传片各多少次，才能使得收视观众最多？

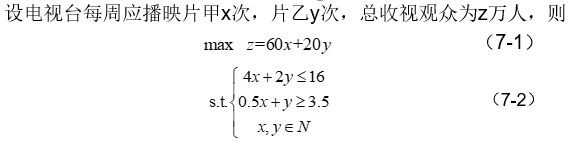
这里变量x、y 称之为决策变量，式（7-1）被称为问题的目标函数，式（7-2）中的几个不等式是问题的约束条件，记为 s.t.。上述即为一规划问题数学模型的三个要素。由于上面的目标函数及约束条件均为线性函数，故被称为线性规划问题。

标准形式：求目标函数的min，约束条件的不等号为小于号

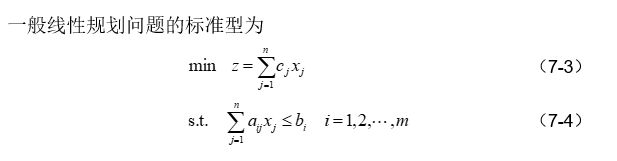
可行解：满足约束条件式（7-4）的解，称为线性规划问题的可行解，而使目标函数（7-3）达到最小值的可行解叫最优解。
可行域：所有可行解构成的集合称为问题的可行域，记为R。
3.线性规划的MATLAB解法
函数：
[x,y]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
它的返回值是向量x，
y为返回目标函数的值；
c为目标函数的系数；
A为约束条件的系数；
b为约束条件和目标函数的常数；
Aeq和beq对应等式约束Aeq * x=beq，若没有，也不可以省略；
LB和UB分别是变量x的上界和下界；
X0是x的初始值；
OPTIONS是控制参数。
例题
(1)


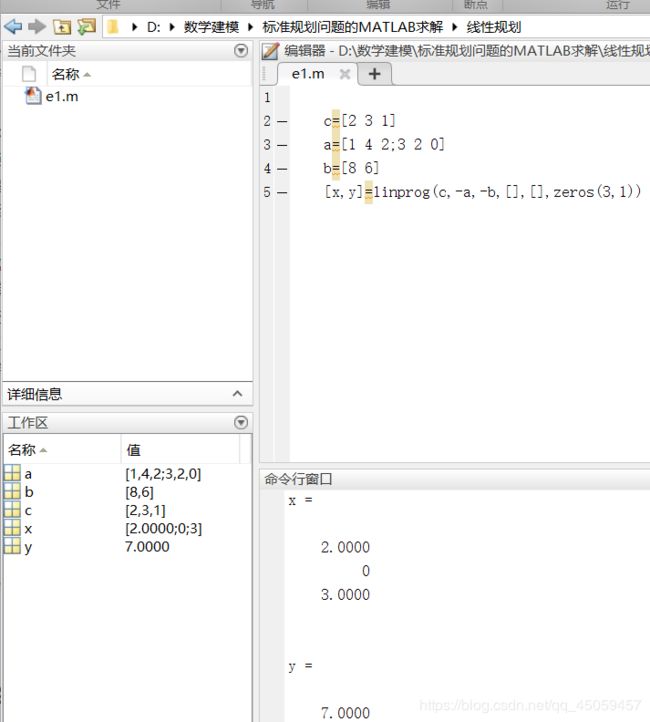
问：为什么a，b要加’-‘，c为什么不用加‘-’？
答：标准形式：求目标函数的min，约束条件的不等号为小于号，而题目是求目标函数的min，约束条件的不等号为大于号，c符合标准形式，约束条件不符合标准形式，所以c不用加‘-’，a，b要加’-‘。
(2)


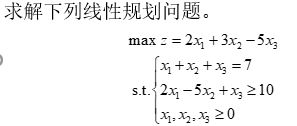
总结：凡是与标准形式不同的，需要加‘-’。
(3)


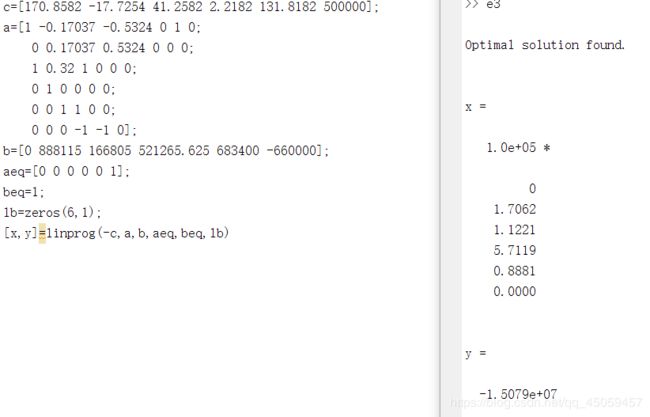
注意点：
1.把目标函数的常数放到约束条件的常数中
2.添加常数标量x6
aeq=[0 0 0 0 0 1];
beq=1;

二、非线性规划

非线性规划目前还没有适于各种问题的一般算法，各个方法都有自己特定的适用范围。所以非线性规划方法很多。
线性规划VS非线性规划
线性规划与非线性规划的区别 如果线性规划的优解存在，其优解只能在其可行域的边界上达到（特别是可行 域的顶点上达到）；而非线性规划的优解（如果优解存在）则可能在其可行域的任 意一点达到。

1.含义：

如果目标函数或约束条件中包含非线性函数，就称这种规划问题为非线性规划问题，简记为NP 。

2.初步了解：

非线性规划问题的一般形式为：

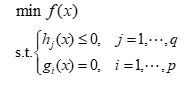
x称为模型的决策变量，f(x)称为目标函数，hj(x)和gi(x)称为约束函数。gi(x)称为等式约束，hj(x)称为不等式约束。
3.fmincon函数
x=fmincon(fun1,x0,A,B,Aeq,Beq,lb,ub,fun2,options)
x为返回值，fun1是定义函数f(x)，x0是x的初始值，A,B,Aeq,Beq定义了线性约束，lb,ub是变量x的下界和上界，fun2是非线性向量函数，options定义了优化参数。

3.深入理解 非线性规划的 Matlab 解法

Matlab 中非线性规划的数学模型写成以下形式



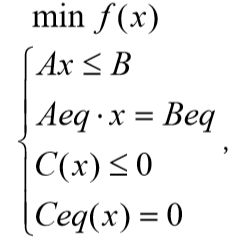
例1：
求下列非线性规划问题。

解题步骤：
(1)编写fun1目标函数和fun2约束函数。
fun1:
function f=fun1(x);
f=x(1)^ 2+x(2)^2+8;
fun2:
function [g,h]=fun2(x);
g=-x(1)^ 2+x(2)^2+2;
h=-x(1)-x(2)^2+2
(2)在MATLAB的命令窗口依次输入
[x,y]=fmincon(‘fun1’,rand(2,1),[],[],[],[],zeros(2,1),[],‘fun2’)
总结：
1.注意文件名，文件名就是被调用的名字。
2.需要初始值。
3.A,B,Aeq,Beq线性约束，lb,ub下界和上界，不能省略！
4.注意非线性向量函数的符号！
例2

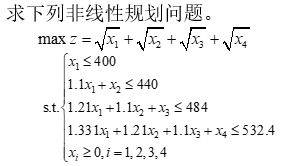
解题步骤：
(1)编写fun3目标函数和fun4约束函数。
function f=fun3(x);
f=-(sqrt(x(1))+sqrt(x(2))+sqrt(x(3))+sqrt(x(4)));

function [g,ceq]=fun4(x);
g(1)=1.1x(1)+x(2)-440;
g(2)=1.21x(1)+1.1x(2)+x(3)-484;
g(3)=1.331x(1)+1.21x(2)+1.1x(3)+x(4)-532.4;
ceq=0;
(2)在MATLAB的命令窗口依次输入
[x,y]=fmincon(‘fun3’,[1 1 1 1],[],[],[],[],[0 0 0 0],[],‘fun4’)

注意点
1.题目是max，不符合标准形式，所以在写标量函数时要加“-”，最后的结果要取相反数，即43.0860。
2.ceq非线性函数不能少，ceq=0都行！

4.Matlab 求无约束极值问题

在 Matlab 工具箱中，用于求解无约束极值问题的函数有 fminunc 和 fminsearch，用法介绍如下。


例3
求f(x)=x(1)^ 3-x(2)^3+3x(1) ^2+3x(2) ^2-9*x(1)的极值。

f=@(x) x(1)^ 3-x(2)^ 3+3x(1)^ 2+3x(2)^2-9*x(1);
[x,z1]=fminunc(f,rand(2,1))
g=@(x)-f(x)
[x,z2]=fminsearch(g,rand(2,1))

z1为极小值，极大值为-z2。

5.二次规划

(1)若某非线性规划的目标函数为自变量x的二次函数，约束条件又全是线性的，就称这种规划为二次规划。
MATLAB中二次规划的数学模型为：

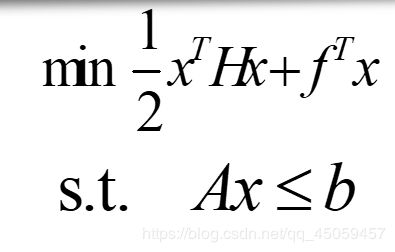
其中，f，b是列向量，A 是相应维数的矩阵，H是实对数矩阵。
注：
函数：
[X,FVAL]= QUADPROG(H,f,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
其中，X的返回值是向量x，FVAL的返回值是目标函数在X处的值。
例4

h=[4,-4;-4,8];
f=[-6;-3];
a=[1 2;4 1];
b=[3;9];
[x,value]=quadprog(h,f,a,b,[],[],zeros(2,1))

x =

1.6500
0.6750

value =

-9.1125
总结：
1.注意补上1/2
2.H实对称矩阵要从二次项凑出来
3.f是一次项前的系数
4.a为约束函数的未知数前的系数，b为约束函数的常数。
(2)罚函数法
利用罚函数法，可将非线性规划问题的求解转化为求解一系列无约束极值问题，因而也称这种方法为序列无约束最小化技术，简记为 SUMT。
罚函数法求解非线性规划问题的思想：利用问题中的约束函数作出适当的罚函数，由此构造出带参数的增广目标函数，把问题转化为无约束非线性规划问题。主要有两种形式，一种叫外罚函数法，另一种叫内罚函数法。
例如：
考虑如下问题：


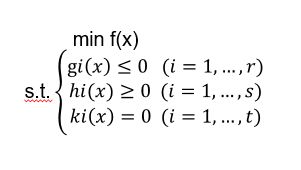
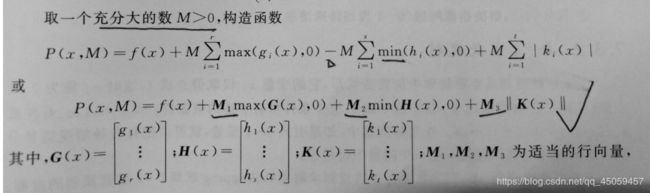
问1：为什么gi(x)取max？
答：如何证明gi(x)<=0，就取gi(x)的最大值，若最大值都<=0，则gi(x)<=0。
例5

解题步骤：
（1）编写M 文件f7.m。

（2）在MATLAB命令窗口输入：

结果：
x =

1.6036
0.6296

y =

10.9705

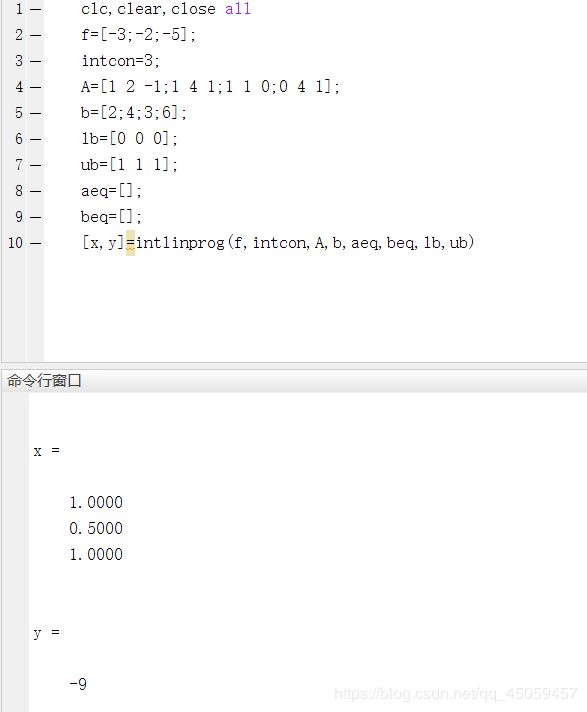
三、整数规划

1.定义
规划中的变量（部分或全部）限制为整数时，称为整数规划。若在线性规划模型中，变量限制为整数，则称为整数线性规划。目前所流行的求解规划的方法，往往只适用于整数线性规划。
2.常见整数规划问题的求解算法有：
(1)分枝定界，可求纯或混合整数线性规划。
(2)割平面法
(3)隐枚举法，求解0-1整数规划。
(4)匈牙利法，解决指派问题（0-1规划特殊情形）

2.0-1整数规划

含义



总结：
1.intcon是未知数的个数
2.aeq，beq不能省，没有就用{[]代替。