【线性代数】矩阵与线性方程组的几何意义

有线性方程组 Ax=b 。本文以三维为例，讨论其物理意义。

解的物理意义

上述线性方程组包含若干个三元一次方程：

a11x1+a12x2+a13x3=b1

a21x1+a22x2+a23x3=b2

a31x1+a32x2+a33x3=b3

...

其中每一个三元一次方程代表三维空间中的一个平面。如果平面个数大于维度，称为超定方程；小于维度，称为欠定方程；等于维度，称为适定方程。
满足这个线性方程组的解 x=[x1,x2,x3] 同时属于所有平面。

线性方程与平面

在进一步矩阵和方程之前，先复习一下三维平面的性质。

如果三元一次方程是齐次的，形如 a1x1+a2x2+a3x3=0 ，则该平面过原点。

证明：易证 [0,0,0] 满足该方程。

过原点的平面平移 [x1¯,x2¯,x3¯] ，变为 a1x1+a2x2+a3x3=a1x1¯+a2x2¯+a3x3¯

证明：系数不变说明角度不变，代入 [x1¯,x2¯,x3¯] 可知平移到此处。

常数项 b 变化时，平面角度不变，只发生平移。

证明：设变化前后有两个平面

a11x+1+a12x2+a13x3=b1

a11x+1+a12x2+a13x3=b′1

两式相减 b1−b′1=0 ，可知两平面无交点，平行。

平面 a1x1+a2x2+a3x3=b 的法向量是 [a1,a2,a3]

证明：将平面方程稍作变化
a1(x1−b/a1)+a2(x2−0)+a3(x3−0)=0
可以看做两个向量的内积
向量1： [a1,a2,a3]
向量2： [x1,x2,x3]−[b/a1,0,0] 。这是连接平面上任一点 [x1,x2,x3] 和平面上固定点 [b/a1,0,0] 的向量。
向量内积为0，说明相互垂直。即平面垂直于法向量。

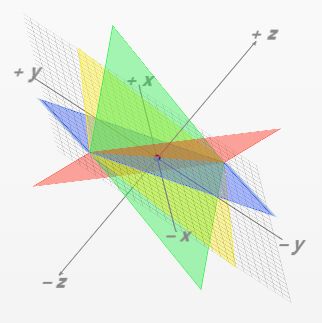
这里有个在线三维绘制工具可以体会一下。

齐次方程组

齐次方程组具有形式 Ax=0 ，平面都是过原点的。根据系数矩阵 A 的秩不同，有以下三种情况。

【情况1】 r(A)=3 。

A 的每一行，即所有平面的法向量 [a11,a12,a13],[a21,a22,a23],[a31,a32,a33]... 能够张成一个三维空间。

平面只有一个交点： [0,0,0] ，线性方程有一个解。

【情况2】 r(A)=2 。
所有平面的法向量，都处于同一个平面内。
由于三个平面都过同一个点 [0,0,0] ，所以他们共有一条交线，线性方程有无穷多解。

这些解共线，换句话说，它们构成了一个二维的子空间。可以用 x=cx¯ 表示。

【情况3】 r(A)=1 。
所有平面的法向量共线。
由于三个平面都过同一个点，所有平面重合于过 [0,0,0] 的平面，线性方程有无穷多解。同样可以用可以用 x=cx¯ 表示。

特别地，当齐次方程组为适定的，即共有三个平面时，上述结论变成我们熟悉的矩阵性质。即如果 r(A)=3 ，则 A 可逆， x=A−1b 。

非齐次方程组

非齐次方程具有形式 Ax=b 。相当于把前述若干平面进行平移。

如果不经限定的平移，一般情况下方程组的解都会变少。只有当所有平面“绑定在一起”平移时，解的情况才不发生变化。

这种情况相当于所有平面都平移 [x1¯,x2¯,x3¯] 。

a11x1+a12x2+a13x3=a11x1¯+a12x2¯+a13x3¯

a21x1+a22x2+a23x3=a21x1¯+a22x2¯+a23x3¯

a31x1+a32x2+a33x3=a31x1¯+a32x2¯+a33x3¯

...

写成矩阵形式

Ax=b=Ax¯

即，常数项 b 可以表示成 A 的列的线性组合，即 b 处于 A 的列空间内。把 A,b 并列组成的增广矩阵 [A;b] 与系数矩阵 A 的秩相同。

从矩阵的角度来说，增加一列不会减少矩阵的秩，即 r(A)≤r([A;b]) 。
如果 r(A)=r([A;b]) ，则 Ax=b 的解的情况和 Ax=0 相同；
如果 r(A)<r([A;b]) ，则 Ax=b 无解。