二维峰值查找

问题描述： 给定一个二维数组，求出其中任意一个峰值。峰值定义为比上下左右都大或相等的元素值（规定数组外无穷小），即 $arr[i][j]$ 为峰值当 $arr[i][j]$ $\ge$ $arr[i-1][j]$ , $arr[i][j]$ $\ge$ $arr[i+1][j]$ , $arr[i][j]$ $\ge$ $arr[i][j-1]$ , $arr[i][j]$ $\ge$ $arr[i][j+1]$ 同时成立。

---

算法思路：分治法（Divide and Conquer）

前提： 对于一个二维数组，若数组内存在元素大于等于数组外围的所有元素，则一定存在峰值。
不靠谱的解释：想象成地形，如果一个区域内有一点比区域四周都要高，则区域内一定存在凸起。因为当从区域四周任意点向那一点走去，无论从哪个方向去，都一定需要往上走。

分治法思想：
1.$divide$ ：拆分问题，将要求解的问题拆分成若干个子问题，子问题需与原问题自相似，即子问题与原问题为同一问题只是规模更小
2.$conquer$ ：求解子问题，若子问题规模足够小可以任意求取则直接返回结果，否则继续拆分问题
3.合并结果：将所有子问题合并得到原问题的解

算法：
对当前要求的二维数组做如下划分，形成四个子区域：

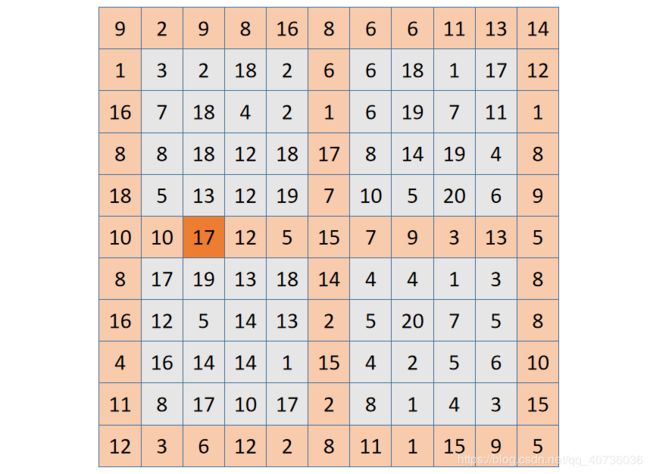
找到 “田” 字上的最大元素，如果它满足条件是峰值，则返回该元素值，否则进入比它大（或等于）的元素所在的区域，递归求解问题。图中 “田” 字上最 大元素为17，下方的19比它大，进入下方的子区域继续求解。

四个区域是新划分出来的子问题，进入的区域根据前面的前提可知一定存在解，且是原问题的解。

---

代码：

#include 
#include 
#include 
#include 
#define _for(i,j,k) for(int i=j;i<=k;i++)
#define for_(i,j,k) for(int i=j;i>=k;i--)
using namespace std;
//find 2D-peak
const int maxn = 2e4+5; //maxsize of the 2D matrix
int arr[maxn][maxn];  //the 2D matrix
int row,column; // the row-size(r) and the column-size of the matrix
int dr[4]={0,0,-1,1};
int dc[4]={-1,1,0,0}; //four directions
//int ar,ac; //keep the location of the peak
int find_2D_peak(int fr,int fc,int tr,int tc){ //from_row,from_column,to_row,to_column ; return the peak
    int mr=(fr+tr)>>1,mc=(fc+tc)>>1,ma=arr[fr][fc],r=fr,c=fc;
      //mid_row     , mid_column  , max_value   ,  row,clumn:the location of the max_value  
    _for(j,fc,tc){
        if(ma<arr[fr][j]) ma=arr[fr][j],r=fr,c=j;
        if(ma<arr[mr][j]) ma=arr[mr][j],r=mr,c=j;
        if(ma<arr[tr][j]) ma=arr[tr][j],r=tr,c=j;
    }
    _for(i,fr,tr){
        if(ma<arr[i][fc]) ma=arr[i][fc],r=i,c=fc;
        if(ma<arr[i][mc]) ma=arr[i][mc],r=i,c=mc;
        if(ma<arr[i][tc]) ma=arr[i][tc],r=i,c=tc;
    }
    int flag=-1;
    _for(i,0,3){
        int nr=r+dr[i],nc=c+dc[i];
        if(nr>=fr&&nr<=tr&&nc>=fc&&nc<=tc&&ma<arr[nr][nc]){
            flag=0;
            break;
        }
    }
    //ar=r;ac=c; update the location of peak
    if(flag) return ma; // case 1
    //case 2
    if(r==fr) flag=c<mc?1:2;
    if(r==mr){
        if(c<mc) flag=ma<arr[r-1][c]?1:3;
        else flag=ma<arr[r-1][c]?2:4;
    }
    if(r==tr) flag=c<mc?3:4;
    if(c==fc) flag=r<mr?1:3;
    if(c==mc){
        if(r<mr) flag=ma<arr[r][c-1]?1:2;
        else flag=ma<arr[r][c-1]?3:4;
    }
    if(c==tc) flag=r<mr?2:4;
    if(flag==1) return find_2D_peak(fr+1,fc+1,mr-1,mc-1);
    if(flag==2) return find_2D_peak(fr+1,mc+1,mr-1,tc-1);
    if(flag==3) return find_2D_peak(mr+1,fc+1,tr-1,mc-1);
    if(flag==4) return find_2D_peak(mr+1,mc+1,tr-1,tc-1);
    return -1; //err
}
int main(){
    cin>>row>>column; //input the size of the 2D matrix
    _for(i,1,row)
    _for(j,1,column) cin>>arr[i][j]; 
    cout<<find_2D_peak(1,1,row,column)<<"\n"; //output one peak
    //cout<
    return 0;
}