聚类分析学习（二）DBSCAN算法学习

一.DBSCAN算法简介

         1.DBSCAN算法是一个比较有代表性的基于密度的聚类算法。

       2.与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据库中发现任意形状的聚类。

         3.基于密度的聚类算法的优点

            (1)可以发现任意形状的簇。

           划分方法和层次方法旨在发现球状簇，它们很难发现任意形状的簇。为了发现任意形状的簇，我们把簇看作数据空间中被稀疏区域分开的稠密区域，即基于密度的聚类算法可发现任意形状的簇，这对于有噪声点的数据有重要作用。

         （2）可以处理噪声点。 （对噪声数据不敏感）

         （3）一次扫描。

         （4）需要密度参数作为终止条件。

       4.基于密度的聚类算法的依据是数据集在空间上的稠密程度，无需事先设定簇的数量。因此特别适合对于未知内容的数据集进行聚类。 

        5.传统基于中心的密度定义

        数据集中特定点的密度通过该点E半径内点的个数估计。显然，密度依赖于半径E。

二.算法中的定义

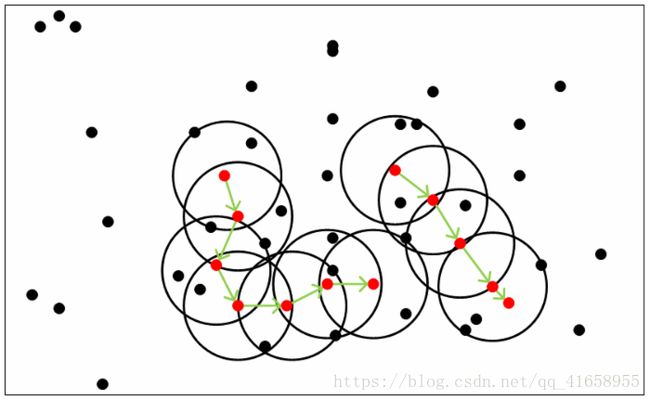
    1.Ε邻域：给定对象半径为Ε内的区域称为该对象的Ε邻域。

    2.核心对象：如果给定对象Ε邻域内的样本点数大于等于MinPts，则称该对象为核心对象。

    3.直接密度可达：对于样本集合D，如果样本点q在p的Ε邻域内，并且p为核心对象，那么对象q从对象p直接密度可达。

   4.密度可达：对于样本集合D，给定一串样本点p1,p2….pn，p= p1,q= pn,假如对象pi从pi-1直接密度可达，那么对象q从对象p密度可达。

    5. 密度相连：存在样本集合D中的一点o，如果对象o到对象p和对象q都是密度可达的，那么p和q密度相连。

   6.密度可达是直接密度可达的传递闭包，并且这种关系是非对称的。密度相连是对称关系。

     DBSCAN目的是找到密度相连对象的最大集合。

  （关于floyd和传递闭包的概念理解参见博客：https://blog.csdn.net/qq_41658955/article/details/81558339）

     （1）传递闭包：设R是X上的二元关系，如果另一个关系R1满足：R1是传递的，R是R1的子集，对于任何可传递关系R11如果有R是R11的子集，就有R1是R11的子集。则称R1是R的传递闭包。即对于一个关系的一个最小的传递关系。

      （2）现在我们来根据（1）中传递闭包的概念推理证明一下：密度可达是不是直接密度可达的传递闭包。（结论A）

             假设R1=对象q到p密度可达；R=对于一系列样本点p1,p2,...,pn，pi到pi-1直接密度可达，p=p1,q=pn。那么我们假设要证明的结论A成立。根据（1）必然满足：

              (a)q到p密度可达关系是传递的。（满足）

            （b）直接密度可达是密度可达的子集。（满足）

            （c）对于任何可传递关系A，有pi到pi-1 直接密度可达是A的子集，则有q到p密度可达是A的子集。

【密度可达非对称的含义是：假设两个对象p和q并且p到q密度可达，但是不一定满足q到p也密度可达，称为非对称关系。

密度相连对称的含义：假设两个对象p和q并且p到q密度相连，一定满足q到p也密度相连，称为对称关系。】

    7.噪声：一个基于密度的簇是基于密度可达性的最大的密度相连对象的集合，不包含在任何簇中的对象被称为噪声。

    8.边界点：该点不是核心对象，但是落在核心对象的某个邻域内，被称为边界点。【根据这个定义，噪声即不是核心对象也不是和核心点的对象】

三.算法指导思想和步骤

（1）指导思想

      密度聚类算法的指导思想是：只要一个区域中点的密度超过某个域值，就把它加到与之相邻的聚类中去。

      对于簇中的每个对象，在给定半径E的邻域中至少要包含最小数目（minPts）个对象。

（2）算法的输入输出：

        1.输入：输入包含n个对象的数据库D，扫描半径eps和最小包含点数minPts。

        2.输出：所有生成的簇，达到密度要求。   

（3）DBSCAN需要二个参数： 扫描半径 (eps)和最小包含点数(minPts)。

任选一个未被访问(unvisited)的点开始，找出与其距离在eps之内(包括eps)的所有附近点。

    1.如果 附近点的数量 ≥ minPts，则当前点与其附近点形成一个簇，并且出发点被标记为已访问(visited)。 然后递归，以相同的方法处理该簇内所有未被标记为已访问(visited)的点，从而对簇进行扩展。

    2.如果 附近点的数量 < minPts，则该点暂时被标记作为噪声点。

    3.如果簇充分地被扩展，即簇内的所有点被标记为已访问，然后用同样的算法去处理未被访问的点。

四.具体算法描述

（1）检测数据库中尚未检查过的对象p，如果p未被处理(归为某个簇或者标记为噪声)，则检查其邻域，若包含的对象数不小于minPts，建立新簇C，将其中的所有点加入候选集N；

（2）对候选集N 中所有尚未被处理的对象q，检查其邻域，若至少包含minPts个对象，则将这些对象加入N；如果q 未归入任何一个簇，则将q 加入C；

（3）重复步骤2)，继续检查N 中未处理的对象，当前候选集N为空；

（4）重复步骤1)~3)，直到所有对象都归入了某个簇或标记为噪声。

五.算法复杂度分析

  1.时间复杂度：算法要对每个对象邻域进行检查，因此时间性能较低。

  （1）基本时间复杂度为O（n*t）【t是找出eps邻域中的点需要的时间】

  （2）最坏情况下时间复杂度为O（n^2）

  （3）在低维空间数据中，一些数据结构如KD树，可以有效检索特定点给定距离内的所有点。从而可以使时间复杂度降低到O（n*logn）

2.空间复杂度：在聚类过程中，DBSCAN一旦找到一个核心对象，就以该核心对象为中心向外扩展，此过程中核心对象将不断增多，没有处理的对象被保存在内存里。若数据库中存在庞大的聚类，将需要很大的内存来储存核心对象的信息，其需求难以预料。

 （1）当数据量增大时，将需要庞大的内存支持，I/O消耗也很大。

 （2）低维或高维数据中，其空间复杂度都是O（n）

六.DBSCAN算法的缺点

   （1）输入参数敏感，确定两个参数E和minPts困难。选取不当易造成聚类质量下降。

   （2）在算法中，两个参数E和minPts全局唯一。当空间聚类的密度不均匀，聚类之间距离相差很大时，聚类质量较差。

   （3）当数据量大时，计算密度单元的计算复杂度大，需要建立空间索引来降低计算量，如KD树。

   （4）对数据维数的伸缩性较差。这类方法需要扫描整个数据库，每个数据对象都可能引起一次查询，因此当数据量大的时候会造成频繁的I/O操作。

七.matlab程序实现

    （1）matlab主程序

%% DBSCAN

clear all;

clc;

 

%% 导入数据集

% data = load('testData.txt');

data = load('testData_2.txt');

 

% 定义参数Eps和MinPts

MinPts = 5;

Eps = epsilon(data, MinPts);

 

[m,n] = size(data);%得到数据的大小

 

x = [(1:m)' data];

[m,n] = size(x);%重新计算数据集的大小

types = zeros(1,m);%用于区分核心点1，边界点0和噪音点-1

dealed = zeros(m,1);%用于判断该点是否处理过,0表示未处理过

dis = calDistance(x(:,2:n));

number = 1;%用于标记类

 

%% 对每一个点进行处理

for i = 1:m

    %找到未处理的点

    if dealed(i) == 0

        xTemp = x(i,:);

        D = dis(i,:);%取得第i个点到其他所有点的距离

        ind = find(D<=Eps);%找到半径Eps内的所有点

        

        %% 区分点的类型

        

        %边界点

        if length(ind) > 1 && length(ind) < MinPts+1

            types(i) = 0;

            class(i) = 0;

        end

        %噪音点

        if length(ind) == 1

            types(i) = -1;

            class(i) = -1;

            dealed(i) = 1;

        end

        %核心点(此处是关键步骤)

        if length(ind) >= MinPts+1

            types(xTemp(1,1)) = 1;

            class(ind) = number;

            

            % 判断核心点是否密度可达

            while ~isempty(ind)

                yTemp = x(ind(1),:);

                dealed(ind(1)) = 1;

                ind(1) = [];

                D = dis(yTemp(1,1),:);%找到与ind(1)之间的距离

                ind_1 = find(D<=Eps);

                

                if length(ind_1)>1%处理非噪音点

                    class(ind_1) = number;

                    if length(ind_1) >= MinPts+1

                        types(yTemp(1,1)) = 1;

                    else

                        types(yTemp(1,1)) = 0;

                    end

                    

                    for j=1:length(ind_1)

                       if dealed(ind_1(j)) == 0

                          dealed(ind_1(j)) = 1;

                          ind=[ind ind_1(j)];   

                          class(ind_1(j))=number;

                       end                    

                   end

                end

            end

            number = number + 1;

        end

    end

end

 

% 最后处理所有未分类的点为噪音点

ind_2 = find(class==0);

class(ind_2) = -1;

types(ind_2) = -1;

 

%% 画出最终的聚类图

hold on

for i = 1:m

    if class(i) == -1

        plot(data(i,1),data(i,2),'.r');

    elseif class(i) == 1

        if types(i) == 1

            plot(data(i,1),data(i,2),'+b');

        else

            plot(data(i,1),data(i,2),'.b');

        end

    elseif class(i) == 2

        if types(i) == 1

            plot(data(i,1),data(i,2),'+g');

        else

            plot(data(i,1),data(i,2),'.g');

        end

    elseif class(i) == 3

        if types(i) == 1

            plot(data(i,1),data(i,2),'+c');

        else

            plot(data(i,1),data(i,2),'.c');

        end

    else

        if types(i) == 1

            plot(data(i,1),data(i,2),'+k');

        else

            plot(data(i,1),data(i,2),'.k');

        end

    end

end

hold off

 

（2）距离计算函数

%% 计算矩阵中点与点之间的距离

function [ dis ] = calDistance( x )

    [m,n] = size(x);

    dis = zeros(m,m);

    

    for i = 1:m

        for j = i:m

            %计算点i和点j之间的欧式距离

            tmp =0;

            for k = 1:n

                tmp = tmp+(x(i,k)-x(j,k)).^2;

            end

            dis(i,j) = sqrt(tmp);

            dis(j,i) = dis(i,j);

        end

    end

end

（3）epsilon函数

function [Eps]=epsilon(x,k)

 

% Function: [Eps]=epsilon(x,k)

%

% Aim: 

% Analytical way of estimating neighborhood radius for DBSCAN

%

% Input: 

% x - data matrix (m,n); m-objects, n-variables

% k - number of objects in a neighborhood of an object

% (minimal number of objects considered as a cluster)

 

 

 

[m,n]=size(x);

 

Eps=((prod(max(x)-min(x))*k*gamma(.5*n+1))/(m*sqrt(pi.^n))).^(1/n);

八.python程序实现

# scoding=utf-8  
import pylab as pl  
from collections import defaultdict,Counter  
  
points = [[int(eachpoint.split("#")[0]), int(eachpoint.split("#")[1])] for eachpoint in open("points","r")]  
  
# 计算每个数据点相邻的数据点，邻域定义为以该点为中心以边长为2*EPs的网格  
Eps = 10  
surroundPoints = defaultdict(list)  
for idx1,point1 in enumerate(points):  
    for idx2,point2 in enumerate(points):  
        if (idx1 < idx2):  
            if(abs(point1[0]-point2[0])<=Eps and abs(point1[1]-point2[1])<=Eps):  
                surroundPoints[idx1].append(idx2)  
                surroundPoints[idx2].append(idx1)  
  
# 定义邻域内相邻的数据点的个数大于4的为核心点  
MinPts = 5  
corePointIdx = [pointIdx for pointIdx,surPointIdxs in surroundPoints.iteritems() if len(surPointIdxs)>=MinPts]  
  
# 邻域内包含某个核心点的非核心点，定义为边界点  
borderPointIdx = []  
for pointIdx,surPointIdxs in surroundPoints.iteritems():  
    if (pointIdx not in corePointIdx):  
        for onesurPointIdx in surPointIdxs:  
            if onesurPointIdx in corePointIdx:  
                borderPointIdx.append(pointIdx)  
                break  
  
# 噪音点既不是边界点也不是核心点  
noisePointIdx = [pointIdx for pointIdx in range(len(points)) if pointIdx not in corePointIdx and pointIdx not in borderPointIdx]  
  
corePoint = [points[pointIdx] for pointIdx in corePointIdx]   
borderPoint = [points[pointIdx] for pointIdx in borderPointIdx]  
noisePoint = [points[pointIdx] for pointIdx in noisePointIdx]  
  
# pl.plot([eachpoint[0] for eachpoint in corePoint], [eachpoint[1] for eachpoint in corePoint], 'or')  
# pl.plot([eachpoint[0] for eachpoint in borderPoint], [eachpoint[1] for eachpoint in borderPoint], 'oy')  
# pl.plot([eachpoint[0] for eachpoint in noisePoint], [eachpoint[1] for eachpoint in noisePoint], 'ok')  
  
groups = [idx for idx in range(len(points))]  
  
# 各个核心点与其邻域内的所有核心点放在同一个簇中  
for pointidx,surroundIdxs in surroundPoints.iteritems():  
    for oneSurroundIdx in surroundIdxs:  
        if (pointidx in corePointIdx and oneSurroundIdx in corePointIdx and pointidx < oneSurroundIdx):  
            for idx in range(len(groups)):  
                if groups[idx] == groups[oneSurroundIdx]:  
                    groups[idx] = groups[pointidx]  
  
# 边界点跟其邻域内的某个核心点放在同一个簇中  
for pointidx,surroundIdxs in surroundPoints.iteritems():  
    for oneSurroundIdx in surroundIdxs:  
        if (pointidx in borderPointIdx and oneSurroundIdx in corePointIdx):  
            groups[pointidx] = groups[oneSurroundIdx]  
            break  
  
# 取簇规模最大的5个簇  
wantGroupNum = 3  
finalGroup = Counter(groups).most_common(3)  
finalGroup = [onecount[0] for onecount in finalGroup]  
  
group1 = [points[idx] for idx in xrange(len(points)) if groups[idx]==finalGroup[0]]  
group2 = [points[idx] for idx in xrange(len(points)) if groups[idx]==finalGroup[1]]  
group3 = [points[idx] for idx in xrange(len(points)) if groups[idx]==finalGroup[2]]  
  
pl.plot([eachpoint[0] for eachpoint in group1], [eachpoint[1] for eachpoint in group1], 'or')  
pl.plot([eachpoint[0] for eachpoint in group2], [eachpoint[1] for eachpoint in group2], 'oy')  
pl.plot([eachpoint[0] for eachpoint in group3], [eachpoint[1] for eachpoint in group3], 'og')  
  
# 打印噪音点，黑色  
pl.plot([eachpoint[0] for eachpoint in noisePoint], [eachpoint[1] for eachpoint in noisePoint], 'ok')     
  
pl.show()  

九.C++程序实现

// DBSCAN.cpp : 定义控制台应用程序的入口点。

//
 
#include "stdafx.h"
#include
#include
#include 
#include 
#include
#include
#include
using namespace std;
 
 
#define DBPOINTTYPE int
 
class dbscan
{
public:
	enum DBState{ unlabeled, core, border, noise };//数据点当前的状态
	struct DBPoint
	{
		int dim;//数据点的维数
		DBState state;
		vectordata;
		vectornear;//该点直接密度可达的点的集合，以dataset索引方式存储
		DBPoint(unsigned int d) :dim(d)
		{
			state = unlabeled;
		}
	};
	struct DBCluster
	{
		int label;//该簇的标号
		setborder;//该簇边界点的集合，以dataset索引方式存储
		setcore;//该簇核心点的集合，以dataset索引方式存储
	};
public:
	dbscan(int minpts, double rad) :MinPts(minpts), radius(rad)
	{
		time_t t;
		srand(time(&t));
	}
	~dbscan();
	void apply();
	void generate_dataset(int datasetsize, int Y, int X);
	void showresult(){
		for (int i = 0; i < clusters.size(); i++)
		{
			char string[100];
			sprintf(string, "第个%d簇：", i);
			cout << string << endl;
			cout << "核心：" << endl;
			for (et::iterator it = clusters[i]->core.begin(); it != clusters[i]->core.end(); it++)
			{
				sprintf(string, "编号%d   ", *it);
				cout << tring << "(" << dataset[*(it)].data[0] << "," << dataset[*(it)].data[1] << ")" << endl;
			}
			cout << "边界：" << endl;
			for (se::iterator it = clusters[i]->border.begin(); it != clusters[i]->border.end(); it++)
			{
				sprintf(string, "编号%d   ", *it);
				cout << string < *it << "(" << dataset[*(it)].data[0] << "," << dataset[*(it)].data[1] << ")" << endl;
			}
			cout << endl << endl;
		}
	}
 
private:
	int MinPts;
	double radius;
 
	vectordataset;
	vectorclusters;
 
private:
	//bool isdensityconnected(DBCluster&cluster1, DBCluster&cluster2);//密度相连
	bool iscore(DBPoint&point);
	bool iscore(int k);
	double distance(DBPoint&point1, DBPoint&point2)
	{
		double dis = 0;
		for (int i = 0; i < point1.dim; i++)
			dis += pow(point1.data[i] - point2.data[i], 2.0);
		return sqrt(dis);
	}
	void expand(int i, DBCluster*clus);
	void mergecluster(int k1, int k2);//合并密度相连的两个簇
};
 
void dbscan::mergecluster(int k1, int k2)
{
 
	clusters[k1]->core.insert(clusters[k2]->core.begin(), clusters[k2]->core.end());
	clusters[k1]->border.insert(clusters[k2]->border.begin(), clusters[k2->border.end());
	for (int i = k2 + 1; i < clusters.size(); i++)
		clusters[i]->label--;
}
 
void dbscan::generate_dataset(int datasetsize, int Y, int X)
{
 
	for (int i = 0; i < datasetsize; i++)
	{
		DBPoint point(2);
		point.data.resize(2);
		point.data[0] = X*double(rand()) / double(RAND_MAX + 1.0);
		point.data[1] = Y*double(rand()) / double(RAND_MAX + 1.0);
		dataset.push_back(point);
	}
}
 
 
 
void dbscan::apply()
{
	int k = 0;
 	while (k < dataset.size() - 1)
	{
		for (int i = k + 1; i < dataset.size(); i++)
		{
			double dis = distance(dataset[k], dataset[i]);
			if (dis < radius)
			{
				dataset[k].near.push_back(i);
				dataset[i].near.push_back(k);
			}
		}
		k++;
	}
	for (int i = 0; i < dataset.size(); i++)	{
		if (iscore(dataset[i]) && dataset[i].state == unlabeled)
		{
			DBCluster*clus = new DBCluster;
			clus->label = clusters.size();
			expand(i, clus);
			clusters.push_back(clus);
		}
	}
	for (int i = 0; i < dataset.size(); i++)
	{
		if (dataset[i].state == unlabeled)
			dataset[i].state = noise;
	}
	/*k = 0;
	while (k < clusters.size() - 1)//合并密度相连的集合
	{
	for (int i = k + 1; i < clusters.size(); i++)
	{
	if (!clusters[i]->core.empty() && !clusters[k]->core.empty())
	{
	setaa;
	//insert_iterator > >res_ins(aa, aa.begin());
	set_union(clusters[i]->border.begin(), clusters[i]->border.end(),//求并集

clusters[k]->border.begin(), clusters[k]->border.end(), inserter(aa, aa.begin()));
	if (aa.size() != clusters[i]->border.size() + clusters[k]->border.size())//密度连
	mergecluster(k, i);
	}
	}
	}
	for (int i = 0; i < clusters.size(); i++)
	{
	if (clusters[i]->core.empty())
	{
	delete clusters[i];
	clusters.erase(clusters.begin() + i, clusters.begin() + i + 1);
	}
	}*/
	//下面验证一下结果
	int sum = 0;
	for (int i = 0; i < clusters.size(); i++)
	{
		sum += clusters[i]->border.size() + clusters[i]->core.size();
	}
	for (int i = 0; i < dataset.size(); i++)
	{
		if (dataset[i].state == noise)
			sum++;
	}
	_ASSERTE(sum == dataset.size());
 
}
 
bool dbscan::iscore(DBPoint&point)
{
	return point.near.size() >= MinPts;
}
bool dbscan::iscore(int k)
{
	return dataset[k].near.size() >= MinPts;
}
 
/*void dbscan::expand(int k, DBCluster*clus)
{
if (clus->core.find(k) == clus->core.end())
{
clus->core.insert(k);//直接密度可达或者密度可达
dataset[k].state = core;
for (int i = 0; i < dataset[k].near.size(); i++)
{
if (!iscore(dataset[k].near[i]) && clus->border.find(i) == clus->border.end())
{
clus->border.insert(dataset[k].near[i]);//直接密度可达
dataset[i].state = border;
}
if (iscore(dataset[k].near[i]))
expand(dataset[k].near[i], clus);
}
}
}*/
 
 
void dbscan::expand(int k, DBCluster*clus)
{
	vectoraa, bb;
	aa.push_back(k);
	while (!aa.empty())
	{
		int gg = aa.back();
		aa.pop_back();
		if (iscore(dataset[gg]) && clus->core.find(gg) == clus->core.end())
		{
			clus->core.insert(gg);
			dataset[gg].state = core;

		for (int i = 0; i < dataset[gg].near.size(); i++)//只有核心对象可以扩展
			{
				if (dataset[dataset[gg].near[i]].state == unlabeled)
					aa.insert(aa.end(), dataset[gg].near[i]);
			}
		}
		else if (!iscore(dataset[gg]) && clus->border.find(gg) ==clus->border.end())
		{
			clus->border.insert(gg);
			dataset[gg].state = border;
		}
	}
}
 
dbscan::~dbscan()
{
	for (int i = 0; i < clusters.size(); i++)
		delete clusters[i];
}
 
 
 
 
int _tmain(int argc, _TCHAR* argv[])
{
 
	/*setaa;
	aa.insert(10);
	aa.insert(25);
	aa.insert(35); aa.insert(5);

	setbb;
	bb.insert(10);
	bb.insert(25);
	bb.insert(35); bb.insert(99);
	setcc;
	set_union(aa.begin(), aa.end(), bb.begin(), bb.end(), inserter(cc, cc.begin()));

	vectordd;
	dd.push_back(24);
	dd.insert(dd.begin(), aa.begin(), aa.end());

	setee;
	ee.insert(10);
	ee.insert(250);
	aa.insert(ee.begin(), ee.end());

	set::iterator it;
	for (it = aa.begin(); it != aa.end(); it++)
	cout << *it << endl;*/
	dbscan db(4, 10);
	db.generate_dataset(100, 100, 100);
	db.apply();
	db.showresult();
 
 
	system("pause");
	return 0;
}

十.推荐博客学习（替大佬打一波广告）

https://blog.csdn.net/u014688145/article/details/53388649