夜深人静写算法（十）- 有向图强连通和2-sat问题

一、引例

  1、同学会

　　【例题1】作者有N个同学，并且N个同学中有M对关系，M对关系描述为(a,b)代表a有b的电话号码(不代表b有a的)。现在作者想举办一次同学会，虽然作者有所有人的电话号码，但是作者这个人比较抠门，不想一个一个打电话浪费电话费。所以如果a能联系到b，b能联系到c，那么作者只需要联系a（b交给a去联系，c交给b去联系即可）。联系第i个同学的电话费为C[i]。求一种方案使得作者需要消耗的总电话费最少(N<=100000，M<=1000000)。

　　（思考一分钟...）

图一-1-1

最少话费为0，因为直接微信联系就可以了，不需要打电话。 哈哈哈哈哈哈哈哈哈哈哈哈！！！！！！！！！

图一-1-2

　　言归正传，我们来仔细分析一下这个问题。把每个同学抽象成图(Graph)的顶点(Vertex)，如果同学a能够联系到同学b，则建立一条a到b的有向边(Edge)。那么，有一些规则是显而易见的：

　　1)如果图中某些顶点的入度为0(这个人不能被任何人联系到)，肯定只能靠作者自己联系了。

　　2)如果构成回路，那么只需要联系回路中花费最小（C[i]最小）的那个人，其它人都可以由他来联系。

图一-1-3

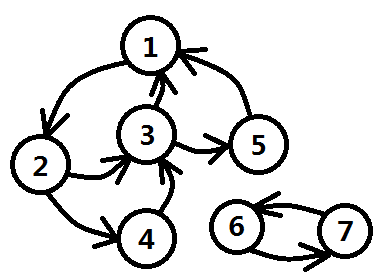
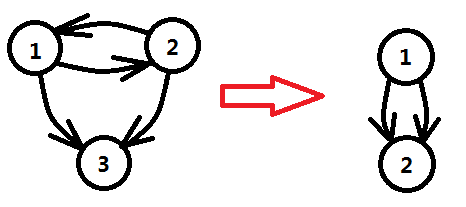
两条规则都比较好理解，第1)条实现比较简单，建边的时候就可以统计一个顶点的入度和出度；但是第2)条规则中的回路就比较模糊了，因为一个点可能属于多个回路，如图一-1-4中，3号结点属于回路1->2->3->1，也属于1->2->3->4->1,同样也属于1->2->3->5->1。那么又产生一个思路：可以将3所在的回路进行归并。即图中1、2、3、4、5这五个结点属于同一个集合。

图一-1-4

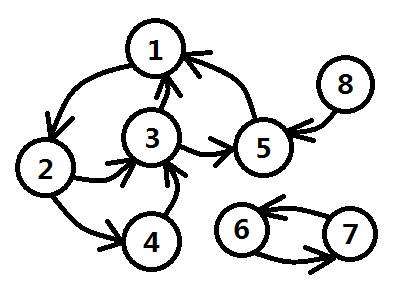
那么我们再来看一种情况，如图一-1-5所示（一个入度为0的点有一条边指向一个属于回路的结点）：

图一-1-5

　　很明显，这种情况下，1、2、3、4、5这五个结点都可以废弃不选了，因为8号必选，而选了8，那么1、2、3、4、5这5个同学都可以通过传递性被“联系”到。综上所述，我们大胆假设，如果一个图是一个有向无环图（DAG），那么只需要找出入度为0的点；否则，可以通过将回路消去转换成DAG图求解。

　　如图一-1-6，首先合并回路1->2->3->1，产生新的结点123（这里为了通俗易懂所以这么编号，实际coding过程可以转换成连续编码，只要之前没有出现过的序号均可），并且将新结点的权值C[123]更新为回路中所有结点的最小值。重复上述步骤，直到整个图是一个有向无环图。

图一-1-6

　　实际编码起来比较复杂，而且复杂度异常高。我们来分析一下，每次找一条回路(采用DFS)，最坏复杂度O(N)；将回路中的点进行集合合并（采用并查集)，最坏复杂度为点集个数，也是O(N)；点合并和点集的边关系需要重新建立，可以做个小技巧，合并后将原先点的进行标记，这样如果访问到标记过的点的那条边就相当于删除了，建立新边关系的复杂度和边数M有关，为O(M)；以上算法只是进行了一次“缩环”，最坏缩环次数为O(N)，所以整个算法的时间复杂度为O(N(N+M))，完全无法接受的时间复杂度。

　　所以我们需要顺着这个思路继续往下走，我们来看一个很重要的性质：如果某些点属于同一个集合，那么集合中的点必然相互可达，这是由回路的性质决定的。这就是本文的重点内容-有向图强连通分量。

二、有向图强连通

  1、有向图强连通分量

　　我们可以继续把这条性质描述为：如果一个有向图中顶点u能够通过一些路径到达顶点v，并且v也可以通过某些路径到达u，那么我们说u和v属于同一个连通分量。当u、v所在集合最大化时，我们说u和v属于同一个强连通分量。

这里的强连通分量就是我们之前提到的那个点集合，求强连通分量主要有三个主流算法，算法复杂度都是O(V+E)级别的，分别为Kosaraju、Tarjan、Gabow，本文只介绍前两个，Gabow是对Tarjan的扩展，读者可自行百度。

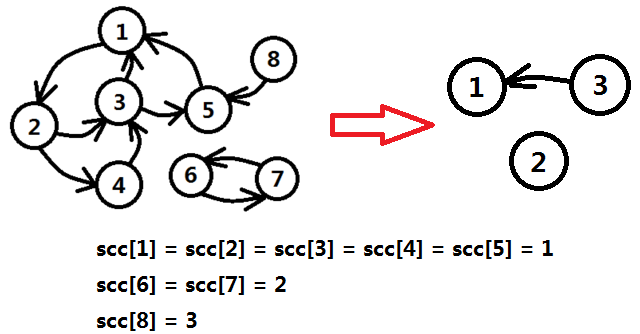
　　算法求出的是原顶点到新顶点编号的一个映射，即数组scc[i]的含义为：原图中i顶点的强连通分量编号为scc[i]。如图二-1-1所示的转换就是原图到新图的一个转化，即缩图的过程，scc[i]数组就是一个映射关系，相当于原图顶点到新图顶点的映射。

图二-1-1

  2、缩图

　　scc[i]代表了映射关系，然而一个图只有顶点是不够的，还需要边。那么新图的边如何构建呢？ 这一步也非常简单，直接枚举原图的所有边集合，对于边E(u,v)，分情况讨论：

　　　　a)scc[u] !=scc[v]，对新图建立E(scc[u],scc[v])；

　　　　b )scc[u]==scc[v]，直接忽略这条边，因为如果建边E(scc[u],scc[v])，则在新图中是一个自环，没什么意义；

　　这个缩图的过程，还需要考虑一种情况，如图所示：

图二-1-2

　　原本没有重边的图，经过缩图以后引入了重边。这种情况，就看实际问题会不会产生影响，如果实际问题对重边可以自行处理，那么大可不必理会；否则，可以采用边哈希去除重边。边哈希的一般做法就是将两个顶点压缩成一个整数然后利用散列哈希。

三、Kosaraju算法

  1、算法背景

　　Kosaraju算法是用于求有向图强连通分量的线性算法，它有效的利用了一个性质：原图的强连通分量和反图的强连通分量一致。算法主体是基于深度优先搜索的。关于深搜的详细内容不再累述，详情参见《夜深人静写算法》系列的第一篇文章：

　　夜深人静写算法（一）-搜索入门

　　2、算法描述

　　数据结构基础：前向星建边，建两张图：原图G和反图G'（反图即对原图的每条边在反图上建立反向边）。

　　　　a)对反图G'求一次后序遍历，按照遍历完毕的先后顺序将所有顶点记录在数组order中。

　　　　b)按照order数组的逆序，对原图G求一次先序遍历，标记连通分量。

　　算法描述就是这么简单，接下来我们进行精密的算法剖析。

　　3、算法剖析

　　　　a.反图的后序遍历

　　　　第一步，先把图建出来，可以利用C++中的STL的vector来存边，也可以自己实现链表。

图三-3-1

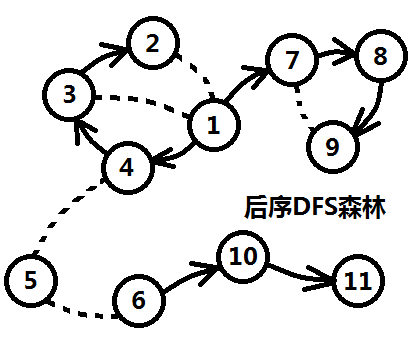
　　对反图G'求一次后序遍历，按照遍历完毕的先后顺序将顶点记录在数组order中。那么对于图三-3-1所示的这张反图，后序遍历的结果数组如下：

图三-3-2

　　这个数组的下标的含义是时间戳，表示的是它和它邻接的结点都被访问完毕的时间。后序遍历保证每个结点只访问一次。

图三-3-3

　　由于每个结点只访问一次，所以如果后序遍历的时候出现了环，那条回边是忽略的，所以无论原先的图是什么，后序遍历，遍历得到的结果是一个森林 （如图三-3-3所示，虚线代表回边，不会被遍历到）。

这个反图的后序遍历结果是三棵树，根结点分别为1、5、6。并且根结点的时间戳在它所在的树中一定是最大的。 （显然，如果原图是一个DAG图，那么后序遍历逆向图G'，求出的order正好是一个原图的拓扑排序，参考原图中的11->10->6）。

　　　b.原图的先序遍历

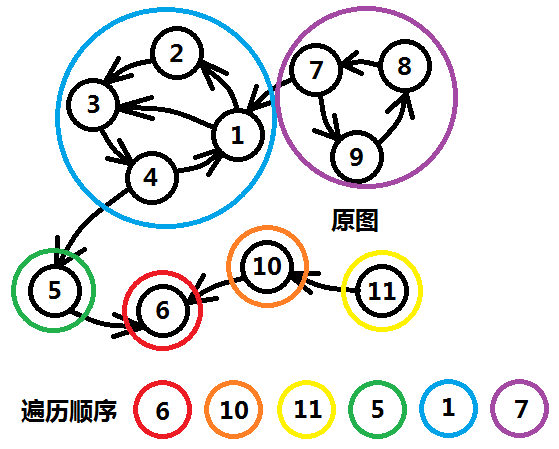
　　　　第二步，按照order的反向顺序，对原图求一次先序遍历。标记连通块。

图三-3-4

图三-3-5

　　两次DFS的时间复杂度均为O(V+E),而且实现起来非常简单。那么，究竟 为什么可以这样求强连通分量？

　　定义：从强连通分量的定义出发，如果两个顶点a和b，a能够到b，b也能够到a，则a和b属于同一个强连通。

对反图上的两个点a和b，如果a能够到b，则a的时间戳大于b，b属于a的DFS树中的子孙结点。 那么如果在原图中，a也能够到b，则说明在反图中b能够到a，又由于原图和反图的强连通一致，所以a和b属于同一个强连通。 那么现在就是要给定a，找出所有能够到达的b。

　　用a->b来表示在搜索树上，a是b的祖先结点，b是a的子孙结点。

　　由于第二次遍历是时间戳大的顶点开始遍历，遍历完标记，所以a能够到达的点的时间戳一定是小于a的时间戳的（大于a时间戳的顶点已经在逆序访问的时候先被标记掉了），令到达的点为b，则b在反图上和a的关系为a->b，这是利用了时间戳的相对大小来确定谁是谁的子孙结点。那么原图a->b，反图也是a->b，所以a和b属于同一个强连通，得证。

这个算法可以说是最简单的算法了，但是理解起来真的有难度。

Kosaraju算法的C++实现

四、Tarjan算法

  1、算法背景

　　Tarjan算法利用了栈的性质，可以在O(V+E)的线性时间内求出有向图的强连通分量。由于只需要一次深度优先遍历，所以无论在算法时间复杂度，还是编码复杂度上，都优于Kosaraju算法。

　　2、算法描述

　　数据结构基础：

　　　　　　栈　　　　　　　　stack[top]　　　　存储正在进行遍历的结点

　　　　　　时间戳数组　　　　　　dfn[u]　　　　结点u第一次被遍历到的时间戳（实际上，每个结点也只会被遍历一次）

　　　　　　追溯数组　　　　　　low[u]　　　　　在遍历时，结点u能够追溯到的祖先结点中时间戳最小的值

　　　　a)对所有未被标记的结点u 调用Tarjan(u) 。

　　　　b)Tarjan(u)是一个深度优先搜索

　　　　　　1)标记dfn[u]和low[u]为当前时间戳，将u入栈；

　　　　　　2)访问和u邻接的所有结点v；

　　　　　　　　如果v未被访问，则递归调用Tarjan(v)，调用完毕更新low[u]=min{low[u],low[v]};

　　　　　　　　如果v在栈中，则更新low[u]=min{low[u],dfn[v]};

　　　　　　3）u邻接结点均访问完毕，如果dfn[u]和low[u]相等，则当前栈中所有结点属于同一个强连通分量，标记scc数组；

　　这个算法比较容易理解，难点在于第2)步的最小值更新，low和dfn容易搞混。不过没事，接下来还是进行一轮精密的算法剖析。

　　3、算法剖析

  快速过一遍Tarjan算法，加深对 dfn数组和low数组的理解 （白色结点为尚未访问的结点；彩色结点为正在访问的结点，并且一定在栈中；灰色结点为访问完毕的结点）。

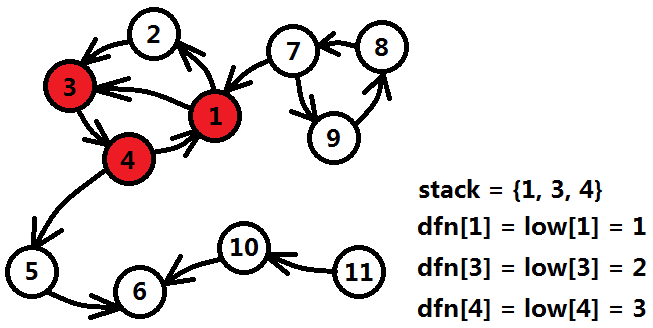
  首先，从1号结点出发，将没有访问过的结点按照深度优先搜索的顺序依次遍历，遍历顺序为1=>3=>4，时间戳数组dfn和追溯数组low分别在访问结点入口更新，元素依次入栈，栈中元素为{1,3,4}。

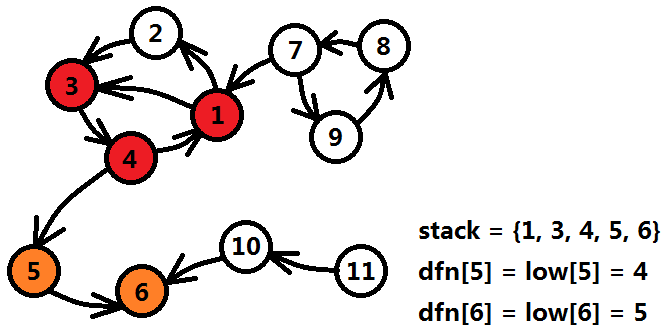
  接着，4号结点继续扩展，发现5号结点；5号结点扩展发现6号结点，同样没有发现什么异样，栈中元素{1,3,4,5,6}。

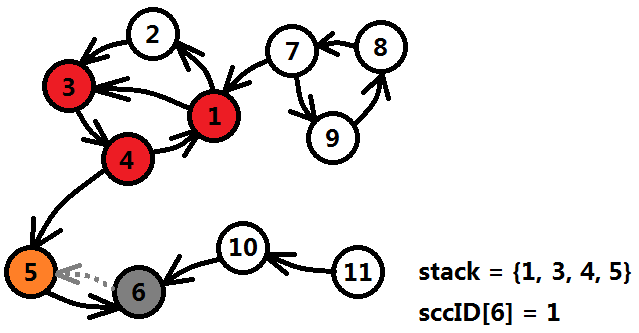
  这时，6号结点发现自己没有出边，并且dfn[6] == low[6]，说明6是一个独立的强连通分量，标记6的强连通编号为1（图中的sccID为强连通编号的映射），将6出栈，6的使命完成了，可以置灰了。

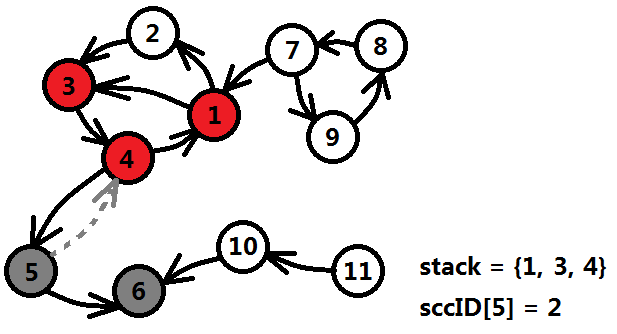
  6号结点回溯到5号结点时（灰色虚线代表回溯），low[5]=min{low[5],low[6]}=4，然后5号结点发现没有其它的边可以遍历，并且dfn[5]==low[5]，说明5也是一个独立的强连通分量，标记5的强连通编号为2，将5出栈并置灰。

  5号结点回溯到4号，没有发生任何事情。

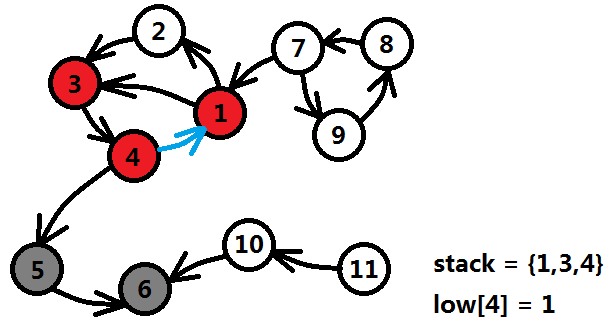
  但是当4号继续遍历它剩余的边时，发现了连到1号结点的边（图中蓝色箭头），这时1号结点还在栈中，也就是1和4必定形成了一个环，那么它们肯定在同一个强连通分量中，更新4号结点的追溯数组low[4]=min{low[4],dfn[1]}=1。

  当4号结点的出边都访问完毕后，low[4]不等于dfn[4]，说明4号结点所在的强连通分量的根还在栈中，先不急，不作任何操作。

  4号结点回溯到3号结点，更新low[3]；3号结点回溯到1号结点，更新low[1]。

  1号结点遍历剩余的边发现2号结点尚未遍历，则扩展2号，并且将2号结点入栈，时间戳为6。

  2号结点遇到了和4号结点一样的情况，还是用蓝色箭头表示它遇上了一个栈中的结点，即3号，3号还没有置灰，说明3号一定能够直接或者间接的访问到2号的祖先，更新low[2]=min{low[2],dfn[3]}=2。

  2号结点回溯到1号结点，1号结点发现没有任何剩余边可以遍历后退出循环，然后判断dfn[1]==low[1]，终极大BOSS终于出现了，将栈中的元素{1,3,4,2}全部出栈，并且标记这些点的强连通编号为3，结点置灰。

  这时我们发现，本次递归已经结束，但是还有白色结点尚未访问。所以Tarjan算法需要在外层套一层轮询，判断每个结点是否被访问，将未被访问的结点作为搜索树的树根，标记已访问，并且执行Tarjan算法。

　　最后献上: Tarjan算法的C++实现

五、2-sat问题

　　【例题2】 给定一些逻辑关系式X　op　Y　=　Z。其中op的取值为(AND,OR,XOR),X,Y,Z的取值为[0,1]，其中X和Y为未知数，给定未知数和关系式的个数(N,M<100000)，求是否存在这样一种解满足所有关系式，存在输出YES,否则NO。

图五-1

　　如图五-1所示，表示X[1]&X[2]=0；X[2]|X[3]=1；X[3]^X[1]=1；那么我们能够肉眼看出来，只要当X[1]=0；X[2]=1；X[3]=1;满足三个方程都成立。那么当未知数和方程茫茫多的时候，我们肉眼就无能为力了。只能靠计算机。

　　朴素算法是枚举，因为每个数的取值只有两种，所以可以枚举每个数是0还是1，然后判断它所在的所有等式中是否满足条件，这个枚举的开销是非常大的，因为每个数都有两种情况，所以总的时间复杂度势必为O(2^N)。

　　对于这类问题，我们可以利用数形结合，将这个数字问题转化成图论问题。

　　1、数形结合

　　首先来看X AND Y，对于这样一个逻辑表达式，我们可以得出这样一个事实：

　　　　a)X　AND　Y=0，可以得出：如果X为1，则Y必定为0；同理，如果Y为1，则X必定为0；

　　　　b)X　AND　Y=1，可以得出：X和Y都为1；我们还可以这样说：如果X为0，则X为1；同理，如果Y为0，则Y为1；

　　基于上面两条，我们将每个变量拆成两个点，一个点表示X=0的情况，一个点表示X=1的情况。

图五-2

　　如图五-2，对于X AND Y = 0的情况，如果X=1则Y=0，建立有向边(X=1)=>(Y=0)，同理(Y=1)=>(X=0)。那么X AND Y = 1的情况，也采用类似的方法建立有向边。 然后我们发现OR和XOR也可以采用类似的方法，建立有向边。

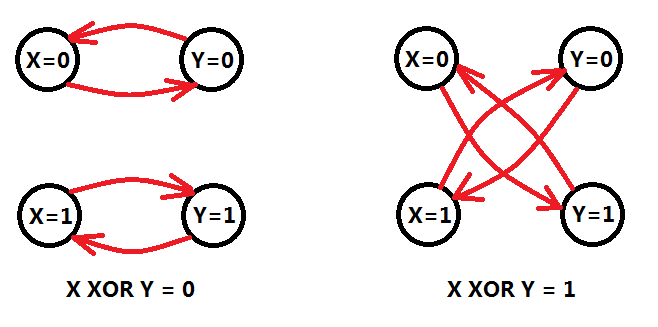
图五-3

图五-4

　　将上述每个等式按照这些规则建立有向边，然后求一次强连通分量。然后一次线性扫描，判断某个点X的两种取值(X=0)和(X=1)如果在同一个强连通分量，则等式组无解，否则必定存在至少一组解。

　　正确性很容易理解，如图五-5所示，还是从定义出发，X=0和X=1位于同一个强连通，则说明当X=0时，可以通过一些步骤推导出X=1；并且当X=1时，又可以推导出X=0；这显然和事实不符。

图五-5

　　2、蕴含式推导

　　最后给出OR关系式的更加严谨的数学推导。

图五-2-1

六、强连通分量相关题集整理

强连通分量相关

迷宫城堡

ProvingEquivalences

EquivalentSets

IntelligenceSystem

Cactus
SummerHoliday

2-sat相关

Party
Wedding

KatuPuzzle

PerfectElection

PriestJohn'sBusiestDay

Ikki'sStoryIV-Panda'sTrick

GetLuffyOut

GetLuffyOut*

Buildingroads

GoDeeper

EliminateT heConflict

BombGame

DivideGroups

MapLabeler
Let'sgohome

PeacefulCommission