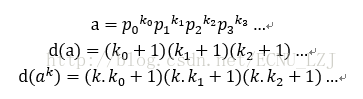(2017多校训练第四场)HDU - 6069 Counting Divisors 区间筛

下面的式子很容易得到。

所以现在我们的问题就是把1e12量级的数字质因数分解，然后算用的素因子个数就行了。注意到一个数字a最小质因子肯定是小于等于根号a的。所以我们只需要打出1到1e6之间的素数表就行了。

如果一个1e12次方量级的数字a，在被[1, 1e6]内的素数分解了之后，剩下的数字还不是1，那么剩下来的那个数字肯定是一个大于1e6的质数。

我们可以选择区间筛的方法，用[1, 1e6]区间内的质数p去筛[a, b]区间内p的倍数q，记录下q如果被p分解，p要使用cnt次，则把k * cnt + 1累加进答案里。最后检验[a, b]区间的数字是不是都被分解成了1，如果不是1，那么肯定是一个大质数，其贡献是k + 1。

比赛的时候我们队是先打出[1, 1e6]区间内的质数表，然后把[a, b]区间内的数字q质因数分解，最后TLE了。这种方法之所以慢，就是因为我们每次要遍历质数，判断当前质数p能不能整除q。算法浪费了太多的时间在那些根本就不能整除q的质数上面，所以TLE了。

代码如下：

#include 

using namespace std;

typedef long long int LL;
const int MOD = 998244353;
const int MAX_N = 1e6 + 5;
const int INF = 0x3f3f3f3f;
int prime[MAX_N], cnt, vis[MAX_N];
LL a, b, k;
LL val[MAX_N], sum[MAX_N];

void init()
{
    memset(vis, 0, sizeof(vis));
    for(int i = 2; i < MAX_N; i++)
    {
        if(!vis[i])
            prime[cnt++] = i;
        for(int j = 0; j < cnt && i * prime[j] < MAX_N; j++)
        {
            vis[i * prime[j]] = 1;
            if(!(i % prime[j]))
                break;
        }
    }
}

int main()
{
    //freopen("test.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    cin.sync_with_stdio(false);
    init();
    int T;
    cin >> T;
    while (T--)
    {
        cin >> a >> b >> k;
        for (LL i = a; i <= b; i++)
        {
            val[i - a] = i;
            sum[i - a] = 1;
        }
        for (int i = 0; i < cnt; i++)
        {
            int p = prime[i];
            for (LL j = a / p * p; j <= b; j += p)
            {
                if (j >= a)
                {
                    int ct = 0;
                    while (val[j - a] % p == 0)
                    {
                        val[j - a] /= p;
                        ct++;
                    }
                    sum[j - a] = (sum[j - a] * ((k * ct + 1) % MOD)) % MOD;
                }
            }
        }
        LL ans = 0;
        for (LL i = a; i <= b; i++)
        {
            if (val[i - a] != 1)
                sum[i - a] = (sum[i - a] * ((k + 1) % MOD)) % MOD;
            ans = (ans + sum[i - a]) % MOD;
        }
        cout << ans << endl;
    }
    return 0;
}