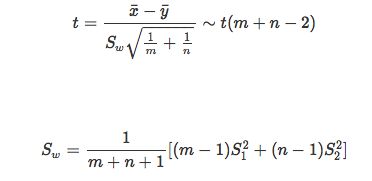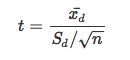T1: t Test

t 检验又叫student t检验（Student’s t test），主要用于样本含量较小（例如n<30），总体标准差σ未知的正态分布。t检验是参数检验的一种。

参数检验：总体分布已知的情况下（可以是给定，也可以是假定），根据样本数据对总体分布的统计参数（均值，方差等）进行推断

t 检验用于检验两个总体的均值差异是否显著，或者一个总体和一个固定值之间的差异。

t 检验原理：

例子：工厂每天可以生产出10万个引擎，我们某天随机抽取了10个引擎，排放水平如下： 
15.6 16.2 22.5 20.5 16.4 19.4 16.6 17.9 12.7 13.9
排放平均值为：(15.6+16.2+22.5+20.5+16.4+19.4+16.6+17.9+12.7+13.9)/10=17.17
那么这天生产的引擎符合20这个排放指标嘛？

先建立两个假设，分别为:
H0:μ⩾20 (原假设)
H1:μ<20 (备择假设)
μ代表平均值

我们假设H0成立，在原假设成立的基础上，求出”取得样本均值或者更极端的均值”的概率，如果概率很大，就倾向于认为原假设H0是正确的，如果概率很小，就倾向于认为原假设H0是错误的，从而接受备择假设H1。

然后计算t-统计量，就是一个标准化的数值
$$t=\frac{\bar{x}-\mu }{S/\sqrt{n}}\sim t(n-1)$$

其中：$\bar{x}$ 表示本次抽样的平均值，$\mu$ 表示总体均值，$S$ 表示本次抽样的标准差，$n$ 表示本次抽样的个数。

计算公式中的这些数值：
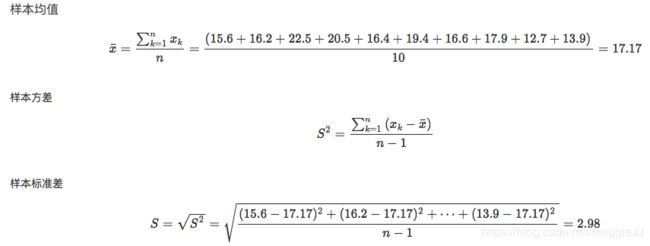注意一个问题，这是无偏估计，除以的n-1

我们把原假设μ⩾20拆分，先考虑μ=20的情况 ，将数值带入t统计量公式中：
$$t=\frac{17.17-20}{2.98/\sqrt{10}}=-3$$
由于t统计量服从自由度为9的t分布，我们可以求出t统计量小于-3.00的概率，即下图阴影部分面积（查表）：


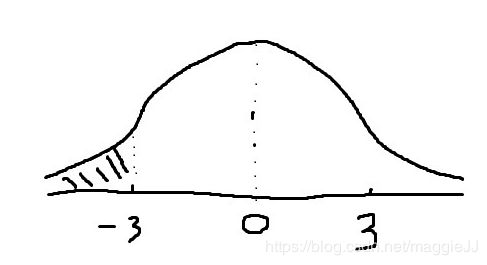
通过查询t分位数表，我们可知，当自由度为9时，t统计量小于-2.821的概率为1%，而我们求得的t统计量为-3.00，所以t统计量小于-3.00的概率比1%还要小(因为-3.00在-2.81的左边，所以阴影面积更小)。

这个概率值通常被称作“p值”，即在原假设成立的前提下，取得“像样本这样，或比样本更加极端的数据”的概率。
到这里，我们可以总结出如下结论： 在μ⩾20成立的前提下，从所有引擎中随机选出10个引擎，这10个引擎排放均值小于17.17的概率小于1%，这个面积就是这个真正的p值。

由于1%的概率很小，所以我们更倾向于认为，原假设H0:μ⩾20是错误的，从而接受备择假设H1。

• I类和II类错误：

上面例子，我们认为1%的概率很小，所以更倾向于认为原假设是错误的，从而接受了备择假设。但这样的判断是准确的吗？

如果事实为H0成立，而我们做出了接受备择假设H1的判断，则犯了第一类错误——拒真 ，也就是假阳性错误
那么我们犯I类错误的概率就是α 【也是拒绝阈，也是p值】， 置信区间就是1-α

如果事实为H1成立，而我们做出了接受原假设H0的判断，则犯了第二类错误——取伪，也就是假阴性错误

t 检验分类

单样本t检验 one sample/group t-test

• 功能：检验一个样本平均数与一个已知的总体平均数差异是否显著
• 条件：

1. 样本来自的总体应服从正态分布；
2. 样本量小于30（当样本量大于30时，用Z统计量，正态分布)

t-统计量：
$$t=\frac{\bar{x}-\mu }{S/\sqrt{n}}\sim t(n-1)$$

其中：$\bar{x}$ 表示本次抽样的平均值，$\mu$ 表示总体均值，$S$ 表示本次抽样的标准差，$n$ 表示本次抽样的个数。

from scipy import stats
# Calculate the T-test for the mean of ONE group of scores.
stats.ttest_1samp(a, popmean, axis=0, nan_policy='propagate')

独立样本t检验 two-sample/group t-test

• 功能：检验两个独立样本所代表的总体均值差异是否显著。
• 条件：

1. 两样本相互独立，即从一总体中抽取一批样本对从另一总体中抽取一批样本没有任何影响，两组样本的个案数目可以不同，个案顺序可以随意调整，即没有配对关系。
2. 样本来自的两个总体应服从正态分布
3. 满足方差齐性（两总体方差相等）

条件检验：

1. 两样本独立性检验，这个根据实验样本可以自己确定
2. 检验样本来自的两个总体是否服从正态分布，可以参考下方 t检验条件判断
3. 检查方差齐性，参考下方t检验条件判断，如果满足方差齐性，做t检验，如果不满足方差齐性，可做：
   《1》：近似t检验：Cochran & Cox法、Satterthwaite法和Welch法
   《2》：秩转换的非参数检验（例如Wilcoxon秩和检验）

t-统计量：



from scipy import stats

# 独立样本t检验，要先检查方差齐性

# Calculate the T-test for the means of *two independent* samples of scores.
# 用levene 检验，如果p <0.05, 则equal_var=False，那么会做 Welch's t-test
stats.ttest_ind(a, b, axis=0, equal_var=True, nan_policy='propagate')

# T-test for means of two independent samples from descriptive statistics.
stats.ttest_ind_from_stats(mean1, std1, nobs1, mean2, std2, nobs2, equal_var=True)

“”“
第一种方法输入两组样本的原始数据的值
第二种方法输入两组数据的统计量，均值，标准差，样本量
”“”

配对样本t检验 paired/matched t-test

• 功能：检验两个配对样本所代表的总体均值差异是否显著。

1.同源配对：
也就是同质的对象分别接受两种不同的处理。
例如：为了验证某种记忆方法对改善儿童对词汇的记忆是否有效，先随机抽取40名学生，再随机分为两组。一组使用该训练方法，一组不使用，三个月后对这两组的学生进行词汇测验，得到数据。问该训练方法是否对提高词汇记忆量有效？


2.自身配对
某组同质对象接受两种不同的处理。例如：某公司推广了一种新的促销方式，实施前和实施后分别统计了员工的业务量，得到数据。试问这种促销方式是否有效？

• 条件：

1. 两样本是配对的（A。两样本观察数目相等；B。两样本的观察顺序不能随意改变）
2. 样本来自的总体应服从正态分布

t-统计量：

from scipy import stats
# Calculate the T-test on TWO RELATED samples of scores, a and b.
stats.ttest_rel(a, b, axis=0, nan_policy='propagate')

t分布
t分布的形状与正态分布很相似，都是中间高，两端低的“钟形”，当t分布的自由度为无穷大时，其形状与正态分布相同，随着自由度的减小，t分布的中间变低，两端变高，与正态分布相比更加“平坦”。

t检验条件判断

1. 抽样的总体是否服从正态分布

对于每一种t检验都需要做这个条件判断，但是很多人不会判断，也没有太大问题，很多时候都是服从正态分布的，不过做一下判断会更严谨的。

• 方法1: scipy.stats.normaltest

该方法基于 D’Agostino and Pearson’s 方法，样本量必须 $\ge 20$ 才有效。结果返回得分值和p值，如果$p<0.05$，那么拒绝零假设，认为该样本不服从正态分布。

• 方法2: Shapiro-Wilk test

Shapiro-Wilk 检验主要用于检验8～50样本量的总体是否服从正态分布，样本量必须 $\ge 3$才有效，结果返回p值和统计量，对于计算得到的p值，如果$p<0.05$，那么拒绝零假设，认为该样本不服从正态分布。

from scipy import stats
# x 是要检测的样本量
# normaltest
k2, p = stats.normaltest(x)
# shapiro-wilk
s, p = stats.shapiro(x)

2. 方差齐性检验 scipy.stats.levene

对于独立样本t检验，要做方差齐性检验， 也就是Bartlett’s test，该检验结果返回统计量和p值，如果$p<0.05$，那么拒绝零假设，认为两个样本方差不齐，不建议做独立样本t检验，将 stats.ttest_ind的参数改为 equal_var=False，则会做 Welch’s t-test检验

from scipy import stats
# x 是要检测的样本量
s, p = stats.levene(x)