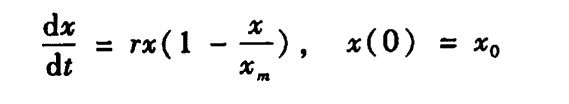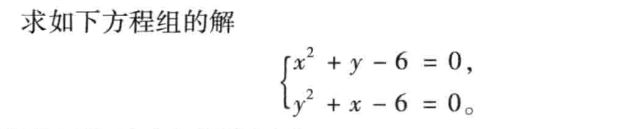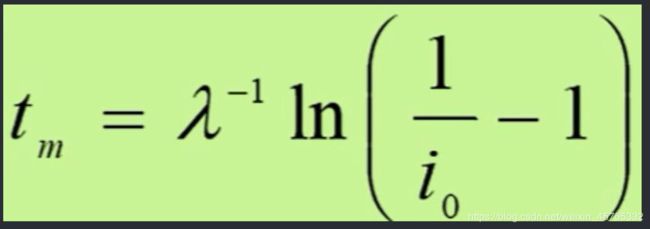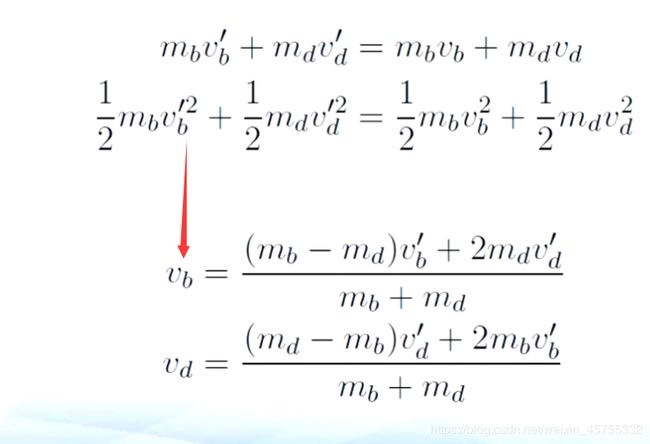MATLAB函数随笔之计算篇
前言:这些都是我在学习MATLAB与数学建模时遇到的一些常用函数,就在这里写了下。当然MATLAB十分强大,函数众多,这些只是凤毛麟角,这篇博客我也会一直更新有新的函数就接着写上,希望对大家有所帮助。有不足之处还望指出。
这里是MATLAB画图篇。
数值计算篇
1. 微分方程
x=dsolve('Dx=r*x*(1-x/m)','x(0)=x0','t')
x =
-m/(exp(log(1 - m/x0) - r*t) - 1)
上面化简一下就是下面这个
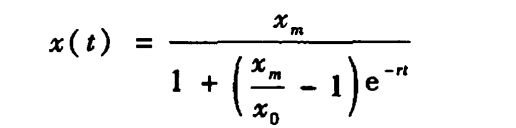
解这个微分方程

求出sym来不要慌,s.x就能给结果了,注意这里是s=,要是ans就是ans.x

本题来源B站大仙一品堂
无约束问题的MATLAB解法
2. 无约束极值问题的符号解
求多元函数 f ( x , y ) = x 3 − y 3 + 3 ∗ x 2 + 3 ∗ y 3 − 9 ∗ x f(x,y)=x^3-y^3+3*x^2+3*y^3-9*x f(x,y)=x3−y3+3∗x2+3∗y3−9∗x的极值
具体为啥这样算,都是高数上的知识
clear
syms x y
% x=-100:100;
% y=-100:100;
f=x.^3-y.^3+3*x.^2+3*y.^2-9*x;
% plot3(x,y,z)
df = jacobian(f);%各求一阶偏导数
d2f = jacobian(df);%号求Hessian阵
[xx,yy] =solve(df) %求驻点
xx = double( xx) ;yy = double(yy);%名转化成双精度浮点型数据,下面判断特征值的正负须是数值型数据
for i =1: length( xx)
a=subs(d2f,{x,y},{xx(i),yy(i)});
b=eig(a);%名求矩阵的特征值
f =subs( f,{x,y},{xx(i),yy(i)});
f = double( f);
if all(b>0)
fprintf('(% f,%f)是极小值点,对应的极小值为 %f\n' ,xx(i),yy(i),f);
elseif all(b<0 )
fprintf('(% f,% f)是极大值点,对应的极大值为%f\n' ,xx(i),yy(i),f);
elseif any(b>0) && any(b<0)
fprintf('(% f,%f)不是极值点\n' ,xx(i),yy(i));
else
fprintf('无法判断(% f,% f)是否是极值点\n',xx(i),yy(i));
end
i=i+1;
end
3.无约束极值问题的数值解
fminunc 找到指定问题的最小值,minxf(x) ,其中f(x)是一个返回一个标量的函数,x是一个向量或者矩阵。
fminsearch 从x0开始,找到函数fun中的局部最小值x,x0可以是标量,向量,矩阵。
求 s i n ( x ) + 3 sin(x)+3 sin(x)+3在4附近的极小值。
clear
f=@(x) sin(x)+3;
[x,y]=fminsearch(f,4)
clc, clear
f=@ (x) x(1)^3 -x(2)^3 +3 *x(1)^2 +3 *x(2)^2 -9 *x(1) ;
g=@ (x) - f(x);
[xy1,z1] = fminunc( f, rand(2,1))%求极小值点
[xy2 ,z2] = fminsearch(g,rand(2,1));%求极大值点
xy2,z2=-z2
xy1 =
1.0000
-0.0000
z1 =
-5.0000
xy2 =
-3.0000
2.0000
ans =
31.0000
可以看到,在(1,0)取得极小值 -5,在(-3,2)取得极大值 31。
4.求函数的零点和方程组的解
求 f ( x ) = x 3 − x 2 + 5 ∗ x − 3 f(x)=x^3-x^2+5*x-3 f(x)=x3−x2+5∗x−3的零点.
xishu=[1 -1 2 -3];
roots(xishu)
ans =
-0.1378 + 1.5273i
-0.1378 - 1.5273i
1.2757 + 0.0000i
求方程组的解
syms x y
[x,y]=solve(x^2+y-6,y^2+x-6)
x =
2
-3
21^(1/2)/2 + 1/2
1/2 - 21^(1/2)/2
y =
2
-3
1/2 - 21^(1/2)/2
21^(1/2)/2 + 1/2
函数化简
( 1 / x 3 + 6 / x 2 + 12 / x + 8 ) ( 1 / 3 ) (1/x^3+6/x^2+12/x+8)^{(1/3)} (1/x3+6/x2+12/x+8)(1/3)
syms x
f=(1/x^3+6/x^2+12/x+8)^(1/3)
r1=simplify(f) %((2*x + 1)^3/x^3)^(1/3)
% 'Steps',默认是1,设置值可以去任意整数,表示化简的轮次
%'IgnoreAnalyticConstraints',默认是false,如果为true,只考虑纯粹的化简,而不顾及“非完全等价”的可能
r2=simplify(f,'Steps',10,'IgnoreAnalyticConstraints',true) %1/x + 2
求极限
s i n ( t ∗ k ) / ( t ∗ k ) , ( 1 − 1 / x ) ( k ∗ x ) sin(t*k)/(t*k),(1-1/x)^{(k*x)} sin(t∗k)/(t∗k),(1−1/x)(k∗x)
syms t x k
g=sin(t*k)/(t*k);
f=(1-1/x)^(k*x);
symvar(g,1) %这个是看一下我们的自由变量是啥 是t
lig=limit(g,0) % t趋近于0时的值
lig1=subs(lig,k,1) % subs是把t替换成1
lif=limit(f,x,inf)
lif1=subs(lif,k,-1)
lif2=vpa(subs(lif,k,-1),48) %vpa是精度,精确到小数点后48位
求导
普通求导: s i n ( ∣ x ∣ ) sin(|x|) sin(∣x∣)
abs()是求绝对值,
Y = sign(x) 返回与 x 大小相同的数组 Y,其中 Y 的每个元素是:
1,前提是 x 的对应元素大于 0。
0,前提是 x 的对应元素等于 0。
-1,前提是 x 的对应元素小于 0。
x./abs(x),前提是 x 为复数。
clear
syms x
x=[-4:0.1:4];
f=sin(abs(x));
d=diff(f)
y=cos(abs(x)).*sign(x);%这里复制了下d
plot(x,y) %这里plot(x,y),y必须重新定义,不能用前面算出来的d
d1 =
cos(abs(x))*sign(x)
隐函数求导
泰勒级数展开
syms x
r5=taylor(x*exp(x)) %默认是6级
r8=taylor(x*exp(x),'Order',8) %这是8级
pretty(r8) %pretty展开多项式的易读格式
有限/无限级数之和.
syms n k
f=1/(k*(k+1))
d1=symsum(f,k,1,inf)
d2=symsum(f,k,1,n)
d1 =
1
d2 =
n/(n + 1)
积分
普通积分
int(x^2)
多重积分
∫ 1 2 ∫ x x 2 ∫ x ∗ y x 2 y x 2 + y 2 + z 2 d z d y d x \int_{1}^{2}\int_{\sqrt{x}}^{x^2}\int_{\sqrt{x*y}}^{x^2y}x^2+y^2+z^2dzdydx ∫12∫xx2∫x∗yx2yx2+y2+z2dzdydx
clear
syms x y z
f=int(int(int(x^2+y^2+z^2,z,sqrt(x*y),x^2*y),y,sqrt(x),x^2),x,1,2)
vpa(f)
符号计算篇
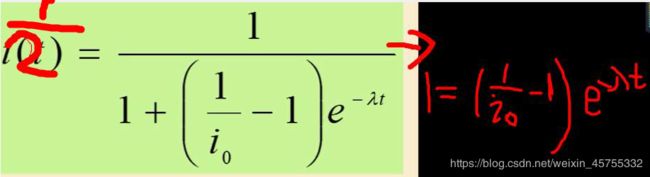
1. 隐函数化简求解
syms t r i
t=solve(1== ((1-i)/i)*exp(-r*t),t)
t =
-log(-i/(i - 1))/r
化简下面函数
syms b d v1 v2 v3 v4
[v3,v4]=solve(b*v1+d*v2==b*v3+d*v4,b*v1^2+d*v2^2==b*v3^2+d*v4^2,v3,v4)
v3 =
(b*v1 - d*v1 + 2*d*v2)/(b + d)
v4 =
(2*b*v1 - b*v2 + d*v2)/(b + d)
用符号法求解
u ∗ w 2 + z ∗ w 2 = v u*w^2+z*w^2=v u∗w2+z∗w2=v
代码很简单,自己运行看结果吧,建议用实时脚本来运行
clear
syms u v w z
E=u*w^2+z*w^2-v
g(z)=u*w^2+z*w^2==v
symvar(E,1)%后面不带数字1的话是给出所有的参数符号,1是最前面那个,也就是我们要求的参数
symvar(g(z),1)
r1=solve(E)
r2=solve(g(z))
s1=solve(E,z)
s2=solve(g(z),z)
ans=simplify(subs(E,z,s1))%subs就是把s1换成z
ans1=simplify(g(s2))
微分方程
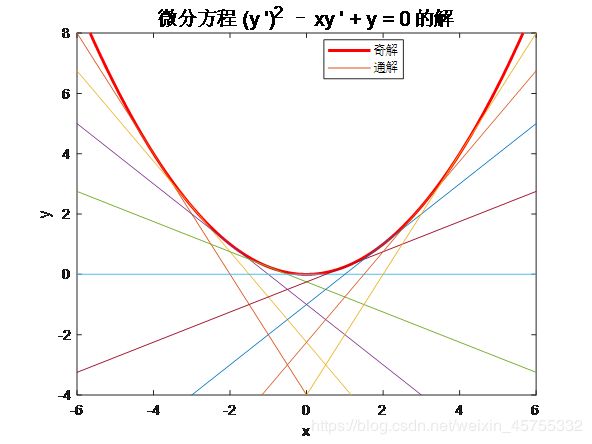
求通解和奇解
图示微分方 y = x y ′ − ( y ′ ) 2 y=xy'-(y')^2 y=xy′−(y′)2的通解和奇解。
(与原微分方程的每一个解都相切的曲线的方程叫奇解)
clear all
y=dsolve('(Dy)^2-x*Dy+y=0','x') %求解,得到一个通解,一个奇解
%%
hold on
hy1=ezplot(y(2),[-6,6,-4,8],1);%奇解的图像
set(hy1,'Color','r','LineWidth',2)
%%
Sv=symvar(y(1)); %自动辨认基本符号变量 (不定常数符号)
for k=-2:0.5:2 %画通解,给基本符号变量赋不同的值
y2=subs(y(1),Sv(1),k);
ezplot(y2,[-6,6,-4,8],1)
end
hold off
box on
legend('奇解','通解','Location','Best')
ylabel('y')
title(['\fontsize{14}微分方程',' (y '')^2 – xy '' + y = 0 ','的解'])
其他函数篇
3. unifrnd生成(连续)均匀分布的随机数
x=unifrnd(0,12,[1,10]);
y=1:10;
plot(y,x,'*')