凸优化学习笔记 4:Convex Function
个人博客 Glooow ,欢迎各位大驾光临
文章目录
- 1. 凸函数
- 1.1 凸函数定义
- 1.2 常见凸函数
- 1.2.1 R R R
- 1.2.2 R n R^n Rn
- 1.2.3 R m × n R^{m\times n} Rm×n
- 2. 凸函数判定
- 2.1 “降维打击”
- 2.2 一阶条件
- 2.3 二阶条件
- 3. Sublevel set & Epigraph
- 4. Jensen's Inequality
1. 凸函数
1.1 凸函数定义
凸函数(convex function)的定义:
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) , ∀ x , y ∈ dom f , θ ∈ [ 0 , 1 ] f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y),\quad \forall x,y\in\text{dom}f,\theta\in[0,1] f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y),∀x,y∈domf,θ∈[0,1]
函数 f f f 的扩展函数(extended-value extension) f ~ \tilde{f} f~ 定义为
f ~ ( x ) = { f ( x ) , x ∈ dom f ∞ , x ∉ dom f \tilde{f}(x)=\begin{cases}f(x),&x\in\text{dom}f\\\infty,&x\notin\text{dom}f\end{cases} f~(x)={f(x),∞,x∈domfx∈/domf
相当于对原来函数 f f f 的定义域进行了扩展。
1.2 常见凸函数
1.2.1 R R R
凸函数(convex)
- 仿射函数 a x + b ax+b ax+b,for any a , b ∈ R a,b\in R a,b∈R
- 指数函数 e a x e^{ax} eax,for any a ∈ R a\in R a∈R
- 幂函数 x α , x ∈ R + + x^\alpha,x\in R_{++} xα,x∈R++,for α ≥ 1 \alpha\ge1 α≥1 or α ≤ 0 \alpha\le0 α≤0
- 绝对值幂函数 ∣ x ∣ p , x ∈ R \vert x\vert^p,x\in R ∣x∣p,x∈R,for p ≥ 1 p\ge 1 p≥1
- 负熵 x log x , x ∈ R + + x\log x,x\in R_{++} xlogx,x∈R++
凹函数(concave)
- 仿射函数 a x + b ax+b ax+b,for any a , b ∈ R a,b\in R a,b∈R
- 幂函数 x α , x ∈ R + + x^\alpha,x\in R_{++} xα,x∈R++,for 0 ≤ α ≤ 1 0\le\alpha\le1 0≤α≤1
- 对数函数 log x , x ∈ R + + \log x,x\in R_{++} logx,x∈R++
1.2.2 R n R^n Rn
- 仿射函数 a T x + b a^Tx+b aTx+b
- 范数 ∥ x ∥ p , p ≥ 1 \Vert x\Vert_p,p\ge 1 ∥x∥p,p≥1
1.2.3 R m × n R^{m\times n} Rm×n
- 仿射函数 f ( X ) = tr ( A T X ) + b f(X)=\text{tr}(A^TX)+b f(X)=tr(ATX)+b
- 谱范数 f ( X ) = ∥ X ∥ 2 = σ m a x ( X ) = ( λ m a x ( X T X ) ) 1 / 2 f(X)=\Vert X\Vert_2=\sigma_{max}(X)=(\lambda_{max}(X^TX))^{1/2} f(X)=∥X∥2=σmax(X)=(λmax(XTX))1/2
2. 凸函数判定
2.1 “降维打击”
“降维打击”是指对于函数 f : R n → R f:R^n\to R f:Rn→R 限制在某一个方向上观察,若对于任意一个方向上都是凸函数,则 f f f 就是凸函数。准确的定义如下。
设 f : R n → R f:R^n\to R f:Rn→R,有映射 g : R → R g:R\to R g:R→R
g ( t ) = f ( x + t v ) , dom g = { t ∣ x + t v ∈ dom f } g(t)=f(x+tv),\quad \text{dom}\ g=\{t|x+tv\in\text{dom}\ f\} g(t)=f(x+tv),dom g={t∣x+tv∈dom f}
则 f f f 为凸函数当且仅当 g ( t ) g(t) g(t) 对任意 x ∈ dom f , v ∈ R n x\in\text{dom}f,v\in R^n x∈domf,v∈Rn 都是凸函数。
例:函数 f : S n → R f:S^n\to R f:Sn→R,有 f ( X ) = log det X , dom f = S + + n f(X)=\log\det X,\text{dom}f=S^n_{++} f(X)=logdetX,domf=S++n
g ( t ) = log det ( X + t V ) = log det X + log det ( I + t X − 1 / 2 V X − 1 / 2 ) = log det X + ∑ i = 1 n log ( 1 + t λ i ) \begin{aligned}g(t)=\log\det(X+tV)&=\log\det X + \log\det(I+tX^{-1/2}VX^{-1/2})\\&=\log\det X + \sum_{i=1}^n \log(1+t\lambda_i)\end{aligned} g(t)=logdet(X+tV)=logdetX+logdet(I+tX−1/2VX−1/2)=logdetX+i=1∑nlog(1+tλi)
由于 g g g 关于 t t t 是凹函数,因此 f f f 是凹函数。
2.2 一阶条件
函数 f f f 为凸函数当且仅当
f ( y ) ≥ f ( x ) + ∇ f T ( x ) ( y − x ) ∀ x , y ∈ dom f f(y)\ge f(x)+\nabla f^T(x)(y-x) \quad \forall x,y\in\text{dom}f f(y)≥f(x)+∇fT(x)(y−x)∀x,y∈domf
证明:略。用定义即可。
2.3 二阶条件
函数 f f f 为凸函数当且仅当海森矩阵(Hessian matrix)(若二阶可微)
∇ 2 f ( x ) ⪰ 0 ∀ x ∈ dom f \nabla^2 f(x)\succeq0 \quad \forall x\in\text{dom}f ∇2f(x)⪰0∀x∈domf
可用海森矩阵验证为凸函数的例子
- 二次函数 f ( x ) = ( 1 / 2 ) x T P x + q T x + r f(x)=(1/2)x^TPx+q^Tx+r f(x)=(1/2)xTPx+qTx+r (with P ∈ S n P\in S^n P∈Sn)
- 最小二乘目标函数 f ( x ) = ∥ A x − b ∥ 2 2 f(x)=\Vert Ax-b\Vert_2^2 f(x)=∥Ax−b∥22
- 二次函数 f ( x , y ) = x 2 / y f(x,y)=x^2/y f(x,y)=x2/y
- log-sum-exp f ( x ) = log ∑ k exp x k f(x)=\log\sum_k\exp x_k f(x)=log∑kexpxk
- 几何均值 f ( x ) = ( Π k x k ) 1 / n f(x)=(\Pi_k x_k)^{1/n} f(x)=(Πkxk)1/n on R + + n R^n_{++} R++n
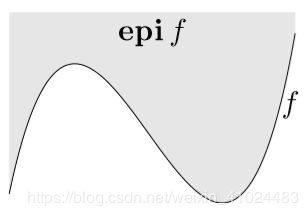
3. Sublevel set & Epigraph
函数 f : R n → R f:R^n\to R f:Rn→R 的 α \alpha α 下水平集( α \alpha α-sublevel set) 的定义为
C α = { x ∈ dom f ∣ f ( x ) ≤ α } C_\alpha=\{x\in\text{dom}f|f(x)\le\alpha\} Cα={x∈domf∣f(x)≤α}
凸函数的下水平集也是凸集,但是反之不一定成立。
针对函数 f : R n → R f:R^n\to R f:Rn→R 定义的 epigraph 为
epi f = { ( x , t ) ∈ R n + 1 ∣ x ∈ dom f , f ( x ) ≤ t } \text{epi}f=\{(x,t)\in R^{n+1}|x\in\text{dom}f,f(x)\le t\} epif={(x,t)∈Rn+1∣x∈domf,f(x)≤t}
函数 f f f 为凸函数当且仅当其 epigraph 为凸集。
Remarks:对于 epigraph 内的点,有
t ≥ f ( y ) ≥ f ( x ) + ∇ f T ( x ) ( y − x ) ⟺ [ ∇ f T ( x ) − 1 ] ( [ y t ] − [ x f ( x ) ] ) ≤ 0 \begin{aligned} t\ge f(y)\ge f(x)+\nabla f^T(x)(y-x) \\ \iff \left[\begin{array}{cc}\nabla f^T(x)\\-1\end{array}\right] \left(\left[\begin{array}{cc}y\\t\end{array}\right] - \left[\begin{array}{cc}x\\f(x)\end{array}\right]\right)\le0 \end{aligned} t≥f(y)≥f(x)+∇fT(x)(y−x)⟺[∇fT(x)−1]([yt]−[xf(x)])≤0
上面的式子实际上就是找到了一个在 ( x , f ( x ) ) (x,f(x)) (x,f(x)) 处的支撑超平面,法向量即为 [ ∇ f T ( x ) − 1 ] T [\begin{array}{cc}\nabla f^T(x) &-1\end{array}]^T [∇fT(x)−1]T
4. Jensen’s Inequality
对于凸函数 f f f,有
f ( E z ) = E f ( z ) f(\mathbb{E}z)=\mathbb{E}f(z) f(Ez)=Ef(z)
证明:离散情况易证,连续情况可以用一阶条件证明。
Lemma: f : R n → R f:R^n\to R f:Rn→R 为凸函数,那么 f f f 在任一内点处都连续(连续但不一定可导)。
Remarks:往往绝大部分点都是可微的,但是我们经常会遇到那些不可微的点,比如 ReLU 函数。