CodeForces - 1269

A. Equation

Let’s call a positive integer composite if it has at least one divisor other than 1 and itself. For example:

the following numbers are composite: 1024, 4, 6, 9;
the following numbers are not composite: 13, 1, 2, 3, 37.
You are given a positive integer n. Find two composite integers a,b such that a−b=n.

It can be proven that solution always exists.

Input
The input contains one integer n (1≤n≤107): the given integer.

Output
Print two composite integers a,b (2≤a,b≤109,a−b=n).

It can be proven, that solution always exists.

If there are several possible solutions, you can print any.

Examples
input
1
output
9 8
input
512
output
4608 4096
题意：
找到两个合数a,b, 满足a-b=n。
直接输出9n和8n即可

#include
#include
using namespace std;
int main(){
	int n;
	scanf("%d",&n);
	printf("%d %d\n",9*n,8*n);
	return 0;
}

B. Modulo Equality

You are given a positive integer m and two integer sequence: a=[a1,a2,…,an] and b=[b1,b2,…,bn]. Both of these sequence have a length n.

Permutation is a sequence of n different positive integers from 1 to n. For example, these sequences are permutations: [1], [1,2], [2,1], [6,7,3,4,1,2,5]. These are not: [0], [1,1], [2,3].

You need to find the non-negative integer x, and increase all elements of ai by x, modulo m (i.e. you want to change ai to (ai+x)modm), so it would be possible to rearrange elements of a to make it equal b, among them you need to find the smallest possible x.

In other words, you need to find the smallest non-negative integer x, for which it is possible to find some permutation p=[p1,p2,…,pn], such that for all 1≤i≤n, (ai+x)modm=bpi, where ymodm — remainder of division of y by m.

For example, if m=3, a=[0,0,2,1],b=[2,0,1,1], you can choose x=1, and a will be equal to [1,1,0,2] and you can rearrange it to make it equal [2,0,1,1], which is equal to b.

Input
The first line contains two integers n,m (1≤n≤2000,1≤m≤109): number of elemens in arrays and m.

The second line contains n integers a1,a2,…,an (0≤ai

The third line contains n integers b1,b2,…,bn (0≤bi

It is guaranteed that there exists some non-negative integer x, such that it would be possible to find some permutation p1,p2,…,pn such that (ai+x)modm=bpi.

Output
Print one integer, the smallest non-negative integer x, such that it would be possible to find some permutation p1,p2,…,pn such that (ai+x)modm=bpi for all 1≤i≤n.

Examples
input
4 3
0 0 2 1
2 0 1 1
output
1
input
3 2
0 0 0
1 1 1
output
1
input
5 10
0 0 0 1 2
2 1 0 0 0
output
0
题意：要求一个数ans，满足a序列的所以数加ans再取余m，使得a序列的一种排列方式与b序列相等。
大暴力，a中的一个数最终一定会变成b中的一个数，所以把a中的某一个数变成b中的数的所有情况都判断一遍即可，答案记得取最小值。

#include
#include
using namespace std;
const int N=2500;
int a[N],b[N],ans[N];
int main() {
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i=0; i<n; ++i)scanf("%d",&a[i]);
	for(int i=0; i<n; ++i)scanf("%d",&b[i]);
	int falg=1;
	sort(a,a+n);
	sort(b,b+n);
	for(int i=0; i<n; ++i) {
		if(a[i]!=b[i]) {
			falg=0;
			break;
		}
	}
	if(falg) {
		printf("%d\n",0);
		return 0;
	}
	int anss=2e9;
	for(int i=0; i<n; ++i) {
		falg=0;
		int cut=(b[i]-a[0]+m)%m;
		for(int j=0;j<n;++j){
			ans[j]=(a[j]+cut)%m;
		}
		sort(ans,ans+n);
		for(int j=0;j<n;++j){
			if(ans[j]!=b[j]){
				falg=1;
				break;
			}
		}
		if(!falg){
			anss=min(anss,cut);
		}
	}
	printf("%d\n",anss);
	return 0;
}

C. Long Beautiful Integer

You are given an integer x of n digits a1,a2,…,an, which make up its decimal notation in order from left to right.

Also, you are given a positive integer k

Let’s call integer b1,b2,…,bm beautiful if bi=bi+k for each i, such that 1≤i≤m−k.

You need to find the smallest beautiful integer y, such that y≥x.

Input
The first line of input contains two integers n,k (2≤n≤200000,1≤k

The next line of input contains n digits a1,a2,…,an (a1≠0, 0≤ai≤9): digits of x.

Output
In the first line print one integer m: the number of digits in y.

In the next line print m digits b1,b2,…,bm (b1≠0, 0≤bi≤9): digits of y.

Examples
input
3 2
353
output
3
353
input
4 2
1234
output
4
1313
题意：求一个字符串，要求这个字符串每k个字符循环一遍，并且这个字符串要比给定字符串大于或等于。
先找出给定字符串的前k个字符，复制到和给定字符串等长，然后判断是否大于等于，否的话，加前k个字符组成的十进制数加一，然后再复制一遍即可。

#include
#include
#include
using namespace std;
string a,b;
int main(){
	int n,k;
	scanf("%d %d",&n,&k);
	cin>>a;
	b=a.substr(0,k);
	for(int i=k;i<n;++i)b+=b[i-k];
	printf("%d\n",n);
	if(b>=a){
		cout<<b;
	}else{
		for(int i=k-1;i>=0;--i){
			if(b[i]=='9'){
				b[i]='0';
			}else{
				b[i]++;
				break;
			}
		}
		for(int i=k;i<n;++i)b[i]=b[i-k];
		cout<<b;
	}
	return 0;
}

D. Domino for Young

ou are given a Young diagram.

Given diagram is a histogram with n columns of lengths a1,a2,…,an (a1≥a2≥…≥an≥1).

Young diagram for a=[3,2,2,2,1].
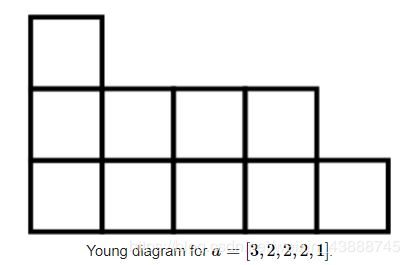
Your goal is to find the largest number of non-overlapping dominos that you can draw inside of this histogram, a domino is a 1×2 or 2×1 rectangle.

Input
The first line of input contain one integer n (1≤n≤300000): the number of columns in the given histogram.

The next line of input contains n integers a1,a2,…,an (1≤ai≤300000,ai≥ai+1): the lengths of columns.

Output
Output one integer: the largest number of non-overlapping dominos that you can draw inside of the given Young diagram.

Example
inputCopy
5
3 2 2 2 1
outputCopy
4
Note
Some of the possible solutions for the example:

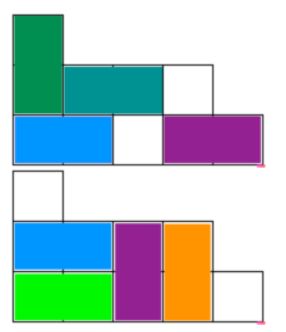
题意：给定一个台阶状的图形，每列的高度给定，且递减，要求这个图形中可以切割出多少个12或21的长方形。
分两种情况：一种是奇数列高度加一除二，偶数列直接除二，结果相加，另一种是奇数列高度直接除二，偶数列加一除二。
如果高度是奇数的话，加一除二必定会多算一个答案，但是下一列如果是偶数的话，还是会多算一个答案，下一列是奇数的话就会补全缺的那一块，所以两种情况必定有一种情况会多数出几个，另一种情况刚刚好是正确答案。

#include
#include
using namespace std;
typedef long long ll;
int main() {
	int n;
	scanf("%d",&n);
	int x;
	ll ans1=0,ans2=0;
	for(int i=0; i<n; ++i) {
		scanf("%d",&x);
		if(i%2) {
			ans1+=x/2;
			ans2+=(x+1)/2;
		} else {
			ans1+=(x+1)/2;
			ans2+=x/2;
		}
	}
	printf("%lld\n",min(ans1,ans2));
	return 0;
}

一场掉分局，被hack了一道题，做题感觉不是太好，思维不行，可能脑子笨吧，学算法让我第一次感觉到我脑子不行，太自闭了，最近烦心事太多了，想快点2020，明年能过得好一点。