AcWing 1131 拯救大兵瑞恩
题目描述:
1944 年,特种兵麦克接到国防部的命令,要求立即赶赴太平洋上的一个孤岛,营救被敌军俘虏的大兵瑞恩。
瑞恩被关押在一个迷宫里,迷宫地形复杂,但幸好麦克得到了迷宫的地形图。
迷宫的外形是一个长方形,其南北方向被划分为 N 行,东西方向被划分为 M 列, 于是整个迷宫被划分为 N×M 个单元。
每一个单元的位置可用一个有序数对 (单元的行号, 单元的列号) 来表示。
南北或东西方向相邻的 2 个单元之间可能互通,也可能有一扇锁着的门,或者是一堵不可逾越的墙。
注意: 门可以从两个方向穿过,即可以看成一条无向边。
迷宫中有一些单元存放着钥匙,同一个单元可能存放 多把钥匙,并且所有的门被分成 P 类,打开同一类的门的钥匙相同,不同类门的钥匙不同。
大兵瑞恩被关押在迷宫的东南角,即 (N,M) 单元里,并已经昏迷。
迷宫只有一个入口,在西北角。
也就是说,麦克可以直接进入 (1,1) 单元。
另外,麦克从一个单元移动到另一个相邻单元的时间为 1,拿取所在单元的钥匙的时间以及用钥匙开门的时间可忽略不计。
试设计一个算法,帮助麦克以最快的方式到达瑞恩所在单元,营救大兵瑞恩。
输入格式
第一行有三个整数,分别表示 N,M,P 的值。
第二行是一个整数 k,表示迷宫中门和墙的总数。
接下来 k 行,每行包含五个整数,Xi1,Yi1,Xi2,Yi2,Gi:当 Gi≥1 时,表示 (Xi1,Yi1) 单元与 (Xi2,Yi2) 单元之间有一扇第 Gi 类的门,当 Gi=0 时,表示 (Xi1,Yi1) 单元与 (Xi2,Yi2) 单元之间有一面不可逾越的墙。
接下来一行,包含一个整数 S,表示迷宫中存放的钥匙的总数。
接下来 S 行,每行包含三个整数 Xi1,Yi1,Qi,表示 (Xi1,Yi1) 单元里存在一个能开启第 Qi 类门的钥匙。
输出格式
输出麦克营救到大兵瑞恩的最短时间。
如果问题无解,则输出 -1。
数据范围
|Xi1−Xi2|+|Yi1−Yi2|=1,
0≤Gi≤P,
1≤Qi≤P
1≤N,M,P≤10,
1≤k≤150
输入样例:
4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2
4 2 1
输出样例:
14
样例解释:
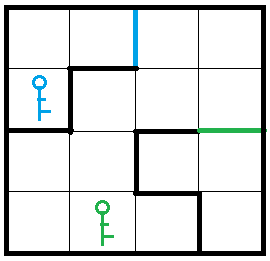
迷宫如下所示:
分析:
本题y总的思路看到一半,发现与自己的想法有所出入,再看下y总的代码,大致理解了其思路,又觉得本题完全可以不用双端队列BFS求解,于是用普通的BFS求解,果然AC了,而且效率也不低。
试想下如果本题没有钥匙和门的条件,只要求从左上角走到右下角的最小步数,就是简单的迷宫问题了,可以使用BFS解决。加上钥匙和门的的条件,便是类似于八数码问题了。实际上BFS解决的最短路问题都可以看作求从初始状态到结束状态需要的最小转移次数,普通迷宫问题的状态就是当前所在的坐标,八数码问题的状态就是当前棋盘的局面。本题在迷宫问题上加上了钥匙和门的条件,显然,处在同一个坐标下,持有钥匙和不持有钥匙就不是同一个状态了,为了能够清楚的表示每个状态,除了当前坐标外还需要加上当前获得的钥匙信息,即f[x][y][st]表示当前处在(x,y)位置下持有钥匙状态为st,将二维坐标压缩成一维就得到f[z][st]这样的状态表示了,或者说,z是格子的编号,从上到下,从左而右的编号依次为1到n*m,st为0110时,表示持有第1,2类钥匙,这里注意我在表示状态时抛弃了最右边的一位,因为钥匙编号从1开始,我想确定是否持有第i类钥匙时,只需要判断st >> i & 1是不是等于1即可。
知道了状态表示,现在题目就转化为了从状态f[1][0]转化为f[n*m][...]状态的最小步数了,我们不关心到达终点是什么状态,只要到达了终点就成功了。现在进行第二步状态转移,两个相邻格子间有墙,就不能转移;有门,持有该类门钥匙就能转移,没有钥匙就不能转移;没有障碍,正常转移。下面讨论转移到有钥匙的格子的情况,这点我与y总处理方式的不同决定了最终解法的不同,y总是先不管有没有钥匙,先转移到这个格子再说,转移到有钥匙的格子的时候步数加一,然后拿起钥匙不移动位置进入另一种状态步数不变。我最初的想法就是,为什么要把这两个过程分开,我们走到有钥匙的格子上,并不用考虑要不要拿钥匙,拿钥匙又不会增加成本,只管拿就行。因此,转移到某个格子时,直接计算下这个格子的状态,格子上有钥匙就在之前状态基础上加上这个钥匙,没有钥匙就继承之前的钥匙状态,这样一来,问题中就不存在边权为0的边了,只要状态转移了,步长都是加一,普通的BFS就可以解决了。
按照DP的一般流程,状态表示和状态转移分析完就可以解决问题了。回想下最开始的摘花生问题,也是从左上角走到右下角,摘尽可能多的花生,是不是这题也能够类似去处理呢?观察摘花生问题条件可以发现,题目限制了只能向下或者向右走,类似的问题也都限制了总步数,这是在为我们用迭代的形式进行状态转移提供方便,而本题可以向上下左右进行状态转移,迭代的形式不好实现,用BFS进行状态转移却很方便。既然本题是类似于八数码问题,自然也可以使用A*算法解决,这里就仅用普通的BFS去求解了。
观察输入的格式,首先读入两个格子坐标以及之间边的类型,读入x1,y1,x2,y2,Gi后,两个格子的坐标可以压缩为z1,z2两个编号,直接g[z1][z2]=g[z2][z1]=Gi即可,因为是双向边,所以要存两次。接着读入哪些坐标放了钥匙,如果一个格子只放一把钥匙,直接key[z] = k即可,但是条件是可以放多把钥匙,就直接用key数组记录下该坐标下存放的所有钥匙的状态吧,读入时key[z] |= k就行了。BFS的过程不再赘述,放进队列里的应该是由格子编号z和持有钥匙状态st构成的二元组,初始状态是{1,key[1]},然后在队列非空时不断出队,取队头元素,尝试向四个方向转移,注意这里我是将格子编号从1开始,因此将其转化为坐标时需要先减一再加一。从0开始编号的话,x = z / m,y = z % m,m是列数;从1开始编号的话x = (z - 1) / m + 1,y = (z - 1) % m + 1,这里从1开始编号的转换特别容易出错。如果转移到棋盘外,或者遇见墙了就不向这个方向转移;如果从当前状态到下一个格子间有门,看下当前状态是否有该类门的钥匙,有就转移,不然不转移。转移到新格子后,新格子上有钥匙就尝试更新下状态,如果新格子的状态之前没有到达过就加入到队列里,到达终点就返回结果。
本题看起来复杂,实际上不过是动态规划、BFS和状态压缩三者的结合,还是比较简单的,总的代码如下:
#include
#include
#include
using namespace std;
const int N = 105,M = 12;
typedef pair PII;
int g[N][N],key[N],d[N][1< q;
int get(int x,int y){
return (x - 1) * m + y;
}
int bfs(){
int t = get(1,1);
q.push({t,key[t]});
st[t][key[t]] = true;
memset(d,0x3f,sizeof d);
d[t][key[t]] = 0;
while(q.size()){
PII u = q.front();
q.pop();
int z = u.first,v = u.second;
for(int i = 0;i < 4;i++){
int x = (z - 1) / m + dx[i] + 1,y = (z - 1) % m + dy[i] + 1;
int v1 = v,z1 = get(x,y);
if(!x || !y || x > n || y > m || !g[z][z1]) continue;//越界或者有墙
if(g[z][z1] != -1){//如果有门
if(!(v >> g[z][z1] & 1)) continue;//没该类门钥匙就不转移
}
v1 |= key[z1];//更新钥匙状态
if(!st[z1][v1]){//每到达过的状态才入队
q.push({z1,v1});
st[z1][v1] = true;
d[z1][v1] = d[z][v] + 1;
}
if(z1 == n * m) return d[z1][v1];//到达终点
}
}
return -1;
}
int main(){
cin>>n>>m>>p;
cin>>k;
int x1,y1,x2,y2,z,z1,z2;
memset(g,-1,sizeof g);//-1表示没有障碍
while(k--){
cin>>x1>>y1>>x2>>y2>>z;
z1 = get(x1,y1),z2 = get(x2,y2);
g[z1][z2] = g[z2][z1] = z;
}
cin>>s;
while(s--){
cin>>x1>>y1>>z;
key[get(x1,y1)] |= 1 << z;
}
cout<