同余问题(2)逆元,孙子定理
定理:如果a,b和c是正整数,且 那么有
那么有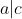
推导: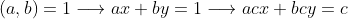
因为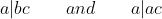 ,所以,
,所以,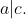
进一步推出结论:如果a,b,c 和m是整数,且m>0,d=(c,m), ,有
,有
推导:

由此产生的新推论:if a,b,c and m are integers such that m>0,(c,m)=1,and , then
, then .
.
数字变大:ifa,b,c and m are integers such that k>0, m>0,and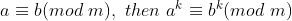
推导:

有趣的相关定理:
if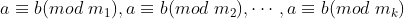 , then
, then {
{  means the least common multiple of
means the least common multiple of  }
}
推导:
%5Ek=%5Cprod%20%5Climits_%7Bi=1%7D%5En%20m_it_i%5C%5Cfor~d=(m_1,m_2,%5Ccdots,m_k),%20d%5Bm_1,m_2,%5Ccdots,m_k%5D=%5Cprod%20%5Climits_%7Bi=1%7D%5En%20m_it_i%5C%5Cthen~(a-b)%5Ek=d%20%5Cprod%20%5Climits_%7Bi=1%7D%5En%20t_i%20%5Bm_1,m_2,%5Ccdots,m_k%5D%5C%5C%5Clongrightarrow%20%5Bm_1,m_2,%5Ccdots,m_k%5D%7Ca-b%20%5Clongrightarrow%20a%20%5Cequiv%20b%20(mod%20%5Bm_1,m_2,%5Ccdots,%20m_k%5D))
由此得出结论,如果所有的mi,mj两两互素,那么
一元线性同余方程 转化成两个变量的线性丢潘图方程: ax+my=b,(a,m)=d, 如果
转化成两个变量的线性丢潘图方程: ax+my=b,(a,m)=d, 如果 那么
那么 没有解,否则有d个解,解是
没有解,否则有d个解,解是 的形式,其中t=0,1,2……d-1 这d个解即是d个模m剩余类
的形式,其中t=0,1,2……d-1 这d个解即是d个模m剩余类
当 中的b=1时,x就是a的逆。对于一元线性同余方程,使用拓展欧几里得可以求出结果,使用逆元也能得出结论。设
中的b=1时,x就是a的逆。对于一元线性同余方程,使用拓展欧几里得可以求出结果,使用逆元也能得出结论。设 那么,
那么, 即
即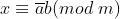 问题就转化成了求解a的逆 若
问题就转化成了求解a的逆 若 那么a就是自身的逆 。这很好理解啊。。(两者联系思考) 这时,
那么a就是自身的逆 。这很好理解啊。。(两者联系思考) 这时,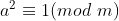 1为模m的二次剩余 【二次剩余: if (a,m)=1,
1为模m的二次剩余 【二次剩余: if (a,m)=1, a为模m的二次剩余】
a为模m的二次剩余】
重要转化: 等价于
等价于
推导:

逆元的递推:设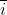 是i模M的一个逆,那么有
是i模M的一个逆,那么有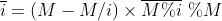 。
。
证明:设
%5C%5Cai%5Cequiv%20-b(mod~M)%5C%5C%5Cfrac%7Ba%7D%7Bb%7D%5Cequiv%20-%20%5Coverline%20i(mod~M)%20%5Clongrightarrow%20a%20%5Ctimes%5Coverline%7BM%5C%25i%7D%20%5Cequiv%20-%5Coverline%7Bi%7D%20(mod~M)%5C%5CM/i%20%5Ctimes%5Coverline%20%7BM%5C%25i%7D%20%5Cequiv%20-%20%5Coverline%20i%20(mod~M)%5C%5C%20%5Coverline%20i%5Cequiv%20-M/i%5Ctimes%20%5Coverline%7BM%5C%25i%7D(mod~M)%5C%5C%20%5Coverline%20i%20%5Cequiv%20(M-M/i)%5Ctimes%20%5Coverline%20%7BM%5C%25i%7D(mod~M)%20%5Clongrightarrow%20%5Coverline%7Bi%7D=(M-M/i)%5Ctimes%20%5Coverline%7BM%5C%25i%7D~%5C%25M)
练习:zoj 3609 Modular Inverse
nefu 84 五指山
中国剩余定理(孙子定理):
对于方程
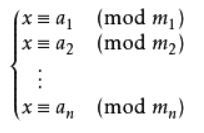
其中两两互素,x具有解: 其中
其中 ,yk是Mk模mk下的逆。很好理解啊。。
,yk是Mk模mk下的逆。很好理解啊。。
令x= n%3=2 , y= n%5=3 ,z= n%7=2
使5×7×a被3除余1,有35×2=70,即a=2;
使3×7×b被5除余1,用21×1=21,即b=1;
使3×5×c被7除余1,用15×1=15,即c=1。
例题: poj 1006 Biorhythms
题意:http://poj.org/problem?id=1006
拓展的问题:一元线性同余方程组,见 http://blog.csdn.net/thearcticocean/article/details/49452859
进一步推出结论:如果a,b,c 和m是整数,且m>0,d=(c,m),
推导:

由此产生的新推论:if a,b,c and m are integers such that m>0,(c,m)=1,and
数字变大:ifa,b,c and m are integers such that k>0, m>0,and
推导:
有趣的相关定理:
if
推导:
由此得出结论,如果所有的mi,mj两两互素,那么
一元线性同余方程
当
重要转化:
推导:

逆元的递推:设
证明:设
练习:zoj 3609 Modular Inverse
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3609
分析:由ax≡1(mod m) 可以得到ax+mk=1,现在要求x的最小正整数,即求上式逆元。
#include
#include
using namespace std;
void extend_Eu(int a,int b,int &f,int &x,int &y){
if(b==0){
x=1;
y=1;
f=a;
return ;
}
extend_Eu(b,a%b,f,x,y);
int t=x;
x=y;
y=t-a/b*y;
}
int main()
{
//freopen("cin.txt","r",stdin);
int T,a,m;
while(cin>>T){
while(T--){
int b,f,x,y;
scanf("%d%d",&a,&m);
b=m;
extend_Eu(a,b,f,x,y);
if(f!=1){ cout<<"Not Exist\n"; continue; } //if(gcd(a,x)!=1)
while(x<0){
x+=b;
}
cout< nefu 84 五指山
http://acm.nefu.edu.cn/JudgeOnline/problemshow.php?problem_id=84
分析:有条件可列出等式,dk1+x=y+nk2 <-->dk1+nk2=y-x 大圣至少要翻的筋斗数就是k1的值。明显,这是拓展欧几里得。(Extend_gcd)
import java.util.*;
public class Main {
static long gcd(long a,long b){
return b!=0?gcd(b,a%b):a;
}
static long Extend_Eulid(long d,long f)
{
long x1=1,x2=0,x3=f,y1=0,y2=1,y3=d ;
while(y3>0 && y3!=1)
{
long q=x3/y3 ;
long t1,t2,t3 ;
t1=x1-q*y1;
t2=x2-q*y2;
t3=x3-q*y3;
x1=y1;
x2=y2;
x3=y3 ;
y1=t1;
y2=t2;
y3=t3 ;
}
if(y3==0)return -1 ;
return y2 ;
}
public static void main(String[] args) {
long t,n,d,x,y;
Scanner sc=new Scanner (System.in);
t=sc.nextLong();
for(int i=0;i中国剩余定理(孙子定理):
对于方程
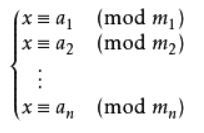
其中两两互素,x具有解:
 其中
其中中国古代求解一次同余式组的方法:
数学著作《孙子算经》卷下第二十六题,叫做“物不知数”问题,原文如下:有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
即:已知 n%3=2, n%5=3, n%7=2, 求n。 (假设除数两两互质)令x= n%3=2 , y= n%5=3 ,z= n%7=2
使5×7×a被3除余1,有35×2=70,即a=2;
使3×7×b被5除余1,用21×1=21,即b=1;
使3×5×c被7除余1,用15×1=15,即c=1。
那么n =(70×x+21×y+15×z)%lcm(3,5,7) = 23 这是n的最小解。
用程序实现:
#include
#include
using namespace std;
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
int get(int a,int b,int c){
int lc=a*b/gcd(a,b),ans=lc;
while(ans%c!=1){
ans+=lc;
}
return ans;
}
int main()
{
int m[3]={3,5,7},n[3]={2,3,2}; //m,n分别代表除数和余数
//int m[3]={23,28,33},n[3]={283,102,23};
int r=gcd(gcd(m[0],m[1]),m[2]),D=m[0]*m[1]*m[2]/r;
int q1=get(m[1],m[2],m[0]),q2=get(m[0],m[2],m[1]),q3=get(m[0],m[1],m[2]);
printf("%d\n",(q1*n[0]+q2*n[1]+q3*n[2])%D);
return 0;
}
例题: poj 1006 Biorhythms
题意:http://poj.org/problem?id=1006
#include
#include
using namespace std;
int get(int a,int b,int c){
int lc=a*b,ans=lc;
while(ans%c!=1){
ans+=lc;
}
return ans;
}
int main()
{
//freopen("cin.txt","r",stdin);
int p,e,i,d,k=0; // 23, 28, and 33
int pd=get(28,33,23),ed=get(23,33,28),id=get(23,28,33);
while(~scanf("%d%d%d%d",&p,&e,&i,&d)){
if(p==-1)break;
int ans=(pd*p+ed*e+id*i)%21252;
ans=(ans-d+21252)%21252; //防止负数的产生。
if(ans==0)ans+=21252; //防止得出的结果和题目给出的日期一样。
printf("Case %d: the next triple peak occurs in %d days.\n",++k,ans);
}
return 0;
}
拓展的问题:一元线性同余方程组,见 http://blog.csdn.net/thearcticocean/article/details/49452859