【2019牛客暑期ACM集训多校第五场】

这场题目其实挺好的。

1.C。BSGS问题，但是如果不离线询问似乎有点卡常，最后队友手写map过了。

#include
using namespace std;
 
struct mymap {
    static const int N=(1<<22);
    int key[N], val[N];
 
    int query(int x) {
        int i = x & (N - 1);
        while (key[i] != -1 && key[i] != x) i = (i + 1) & (N - 1);
        return val[i];
    }
 
    void update(int x, int id) {
        int i = x & (N - 1);
        while (key[i] != -1 && key[i] != x) i = (i + 1) & (N - 1);
        key[i] = x, val[i] = id;
    }
 
    void clear() {
        memset(key, -1, sizeof(key));
        memset(val, -1, sizeof(val));
    }
};
 
inline int qpow(int a,int b,int mod){
    int res=1;
    while(b){
        if(b&1) res=1ll*res*a%mod;
        a=1ll*a*a%mod;
        b>>=1;
    }
    return res;
}
 
// a^x === b   x=lg(a,b)
inline int bsgs_lg(const int a,const int b,const int mod){//
    static mymap mp;
    static int lasta=-1;
 
    int sqr=min(mod/2,int(sqrt(1000ll*mod-1)+1));
    if(lasta!=a) {
        lasta=a;
        mp.clear();
        for(int i=0,qw=1;i x0+ib=v -> ib=v-x0 -> i=(v-x0)/b
                if(v==x0) printf("0\n");
                else if(v==b) printf("1\n");
                else printf("-1\n");
            }
        }
        else if(a==1){
            //xi=x(i-1)+b=x0+ib
            int revb=qpow(b,p-2,p);
            int q; scanf("%d",&q);
            while(q--){
                int v; scanf("%d",&v);// xi=v -> x0+ib=v -> ib=v-x0 -> i=(v-x0)/b
                if(b==0&&v!=x0) printf("-1\n");
                else if(v==x0) printf("0\n");
                else {
                    int ans=1ll*(v-x0+p)*revb%p;
                    if(ans>=n) ans=-1;
                    printf("%d\n",ans);
                }
            }
        }
        else{
            int rev=qpow(a-1,p-2,p);
            int y0=(x0+1ll*b*rev)%p;// yi=y0*(a^i)  yi=xi+b/(a-1)
            int revy0=qpow(y0,p-2,p);
 
            int q; scanf("%d",&q);
            while(q--){
                int v; scanf("%d",&v);// xi=v -> yi=v+b/(a-1)
                v=(v+1ll*b*rev)%p;// v=yi=y0*(a^i)
                v=1ll*v*revy0%p;//a^i=v/y0
                int ans=bsgs_lg(a,v,p);
                if(ans>=n) ans=-1;
                printf("%d\n",ans);
            }
        }
    }
}

2.F题。找一个集合，使得这个集合里任意两个数至少存在两位不相同。对于任意两个数，如果他们二进制位上只有一位不同，给他们连边。这样建出来的图一定是一个二分图，因为可以证明不存在奇环（伪证一下：假设存在奇环，长度位3，x,y,z.那么x和y,z都有一位不一样，y，z要么相等，要么有两位不一样，这样y,z不可能有边存在，所以不存在奇环）这样就是求一个二分图的最大独立集。染色搞一搞就好了。

#include
using namespace std;
const int maxn = 5010;
int a[maxn], b[maxn], n;
struct BinGra
{

	int col[maxn], Left[maxn], Right[maxn], vis[maxn];
	vector G[maxn], ans, tmp;
	//染色。
	void dfs(int u, int color) 
	{
		tmp.push_back(u);
		col[u] = color;
		for (auto v : G[u])
			if (!col[v])
				dfs(v, 3 - color);
	}
	int dfs2(int u) {
		vis[u] = 1;
		for (auto v : G[u])
			if (!vis[v]) {
				vis[v] = 1;
				if (!Left[v] || dfs2(Left[v])) {
					Left[v] = u;
					Right[u] = v;
					return 1;
				}
			}
		return 0;
	}
	void gao() {
		int color = 2;
		for (auto u : tmp)
			if (col[u] == color)
			{
				for (auto v : tmp)
					vis[v] = 0;
				dfs2(u);
			}

		for (auto u : tmp)
			vis[u] = 0;
		for (auto u : tmp)
			if (col[u] == color && !Right[u])
				dfs2(u);
		for (auto u : tmp)
			if ((col[u] == color && vis[u]) || (col[u] == 3 - color && !vis[u]))
				ans.push_back(b[u]);
	}
	//最终结果保存在ans数组里。
	void solve()
	{
		for (int i = 1; i <= n; i++)
		{
			if (col[i])
				continue;
			tmp.clear();
			dfs(i, 1);
			gao();
		}
		printf("%d\n", ans.size());
		for (int i = 0; i < ans.size(); i++)
			printf("%d%c", ans[i], (i == ans.size() - 1) ? '\n' : ' ');
	}
}bg;
int main() {
     
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> a[i], b[i] = a[i];
	sort(b + 1, b + 1 + n);
	for (int i = 1; i <= n; i++)
		a[i] = lower_bound(b + 1, b + 1 + n, a[i]) - b;
	for (int i = 1; i <= n; i++)
		for (int j = 0; j < 30; j++) 
		{
			//枚举一下位数，看看是不是存在只有一位不一样并且在数组内部存在的。
			int x = b[i] ^ (1 << j);
			int k = lower_bound(b + 1, b + 1 + n, x) - b;
			if (b[k] == x)
				bg.G[i].push_back(k);
		}
	bg.solve();
}

3.B题：十进制快速幂。当作一个补充知识点好了。

#include
using namespace std;
 
void mul(const int a[2][2],const int b[2][2],int c[2][2],int mod){
    int res[2][2]={};
    for(int i=0;i<2;i++){
        for(int j=0;j<2;j++){
            for(int k=0;k<2;k++) res[i][j]=(res[i][j]+1ll*a[i][k]*b[k][j])%mod;
        }
    }
    memcpy(c,res,sizeof(res));
}
 
void qpow(const int aa[2][2],int b,int c[2][2],int mod){
    int a[2][2]; memcpy(a,aa,sizeof(a));
    int res[2][2]={
            1,0,
            0,1
    };
    while(b){
        if(b&1) mul(res,a,res,mod);//res=1ll*res*a%mod;
        mul(a,a,a,mod);//a=1ll*a*a%mod;
        b>>=1;
    }
    memcpy(c,res,sizeof(res));
}
 
void qpow(const int aa[2][2],char*b,int ed,int c[2][2],int mod){
    int a[2][2]; memcpy(a,aa,sizeof(a));
    int res[2][2]={
            1,0,
            0,1
    };
    while(ed>=0){
        int t[2][2];
        qpow(a,b[ed]-'0',t,mod); mul(res,t,res,mod);//res=res*qpow(a,b[ed]-'0',mod);
        qpow(a,10,a,mod);
        ed--;// b/=10
    }
    memcpy(c,res,sizeof(res));
}
 
const int maxn=1e6+6;
char s[maxn];
int main(){
    int x0,x1,a,b,mod;
    scanf("%d%d%d%d%s%d",&x0,&x1,&a,&b,s,&mod);
    int trans[2][2]={
            a,b,
            1,0
    };
    int ans[2][2]={
            x1,0,
            x0,0
    };
    int trans2[2][2];
    qpow(trans,s,int(strlen(s))-1,trans2,mod);
    mul(trans2,ans,ans,mod);
    cout<

4.G是一个DP，这个队友秒了，我还没来及看题。

5.H，队友写了，这个题目我看完之后就知道是一个topSort。这和拓扑排序中的一个经典问题是一样的：在一场比赛中给你任意两个人的比赛结果，输出最终比赛结果排名。在局部关系中排在前边的向后边建一条有向边，然后拓扑排序就是答案。（另一个队友开始想错了，搞成了最长路？？？？然后）

6.I是一个计算几何的问题，分析一下做法，代码就不贴了，因为我写的比较丑。

首先这个题目没有说让你找整点，这是一个很重要的地方，我开始以为是找整点？？?

然后保证答案存在，这又很良心。然后我们考虑答案存在时时什么样子的？

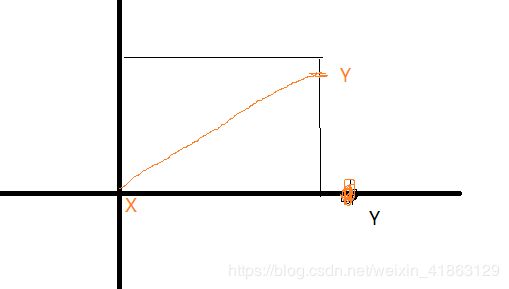
答案存在时，这个三角形可以被放在矩形的内部，不管他在哪里，我们总是可以把坐标系给平移到某一个顶点。这样其实就是可以得到一个固定的点，或者说得到一个结论，我们总是可以在原点构造一个满足条件的三角形。那么现在考虑边，边是不是永远和x重合？不一定，这你要看这条边和w的关系，无非两种情况，重合和不重合。如果重合我们就可以得到另外一个点，要是不重合？我们旋转这条边，使得定点落在另外一条边上。有点抽象？画图展示：

                                                  

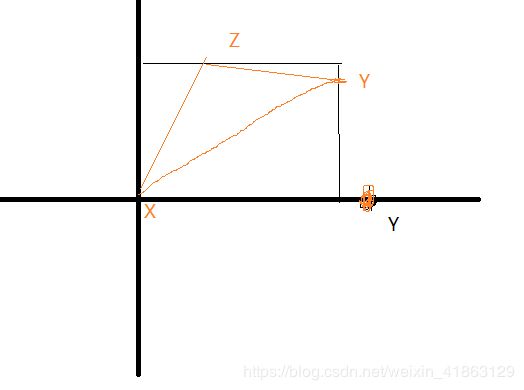
比如XY这条边，大于w，我们把它旋转到另外一条边上去，当然这个操作不一定成立，如果不成立就说明这种方案不合适，换一个。那么其实就有6中情况，

                          

枚举一下X,Y,Z的相对位置，其实就是一个3的排列，然后计算第三个点。比如这里计算Z，其实Z的坐标很好算，Zoy这个夹角等于ZXY和Yxy这两个夹角之和，分别算一下加起来就好了。