层次分析法(AHP)是把问题条理化、层次化,构造出一个有层次的结构模型的方法。
比如要选择旅游地,有3个选择方案,苏杭、北戴河和桂林。选择过程需要考虑多个因素,比如景色、费用、居住、饮食和旅途。
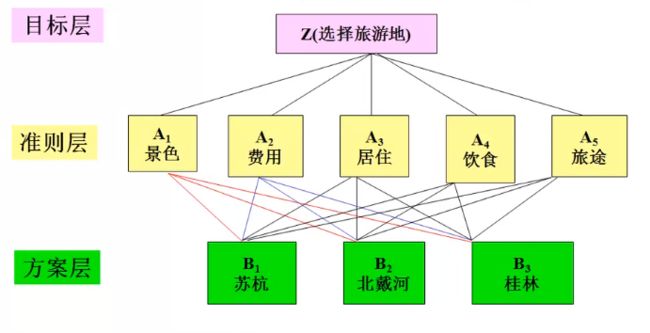
1.分为目标层(选择旅游地),准则层(景色、费用、居住、饮食和旅途)和方案层(苏杭、北戴河和桂林)。层次结构模型如图所示:
2.构造判断矩阵
标度是主观判断的,不同人造出来的矩阵可能不一样。
准则层的矩阵:Ax = [ aij ]; x个n*n的矩阵,此时n=5表示准则层的数量,x表示准则层对目标层的影响,这里x=1。
举例:a14 = 3表示主观认为在选择旅游地时,景色比美食稍重要。反之,a41 = 1/3表示美食比景色稍不重要。
方案层的矩阵:Bx = [ aij ]; x个n*n的矩阵,此时n=3表示方案层的数量,x表示准则层对方案层的影响,这里x=5。
举例:B1中,a13=5表示,在景色方面,苏杭比桂林明显重要。
也就是要构造x+1=6个矩阵。数据如下,是主观假设给出的。
[ 1 1/2 4 3 3; 2 1 7 5 5; 1/4 1/7 1 1/2 1/3; 1/3 1/5 2 1 1; 1/3 1/5 3 1 1 ] [ 1 2 5; 1/2 1 2; 1/5 1/2 1 ] [ 1 1/3 1/8; 3 1 1/3; 8 3 1 ] [ 1 1 3; 1 1 3; 1/3 1/3 1 ] [ 1 3 4; 1/3 1 1; 1/4 1 1 ] [ 1 1 1/4; 1 1 1/4; 4 4 1 ]
3.一致性检验
构造判断矩阵过程可能会构造错误,比如矩阵
1 9 1/3
9 1 5
3 1/5 1
a12 = 9 表示 因素1比因素2极端重要,a31=2表示因素3比因素1稍重要,则重要程度显然是 因素3>因素1>因素2,而a23=5表示因素2比因素3明显重要,矛盾。
并且对于每一个n阶矩阵会得到一个权重矩阵W,W是一个n*1的矩阵,即n个数,比如A矩阵得到的WA矩阵是
[0.26228;
0.47439;
0.054492;
0.098534;
0.1103;]
表示景色、费用、居住、饮食和旅途对于选择旅游地(上一层)的权重比分别是0.26228、0.47439、0.054492、0.098534和0.1103。体现出影响因素的层次。
比如B2得到的WB2矩阵是
[0.08199;
0.23645;
0.68156]
表示苏杭、北戴河和桂林在景色方面的权重比分别是0.08199、0.23645和0.68156。
4.对权值计算做出决策
获得了6个矩阵的权重比,分别是
WA=[0.26228;0.47439;0.054492;0.098534;0.1103];
WB1=[0.59489;0.27661;0.1285];
WB2=[0.08199;0.23645;0.68156];
WB3=[0.42857;0.42857;0.14286];
WB4=[0.63275;0.1924;0.17485];
WB5=[0.16667;0.16667;0.66667];
每一个旅游景点对于目标层Z的权重=准则层权重*方案层权重之和。
苏杭的权重=0.26228*0.59489+0.47439*0.08199+0.054492*0.42857+0.098534*0.63275+0.1103*0.16667=0.29901
北戴河的权重=0.26228*0.27661+0.47439*0.23645+0.054492*0.42857+0.098534*0.1924+0.1103*0.16667=0.24541
桂林的权重=0.26228*0.1285+0.47439*0.68156+0.054492*0.14286+0.098534*0.17485+0.1103*0.66667=0.45558
最后0.29901+0.24541+0.45558=1;
桂林的比重最大,选择去桂林!
代码:
clc
clear all;
disp('请输入判断矩阵A(n阶)');
A = input('A=');
[n,~]=size(A);%由于矩阵构造方法的原因,矩阵都是正方形的所以关于矩阵的大小只需要取一个参数
Asum=sum(A,1);%求每一列的和
Aprogress=A./(ones(n,1)*Asum);%计算每一列个元素在这一列占的比重
W=sum(Aprogress,2)./n;%每一行元素相加取平均值,需要注意这里W是个列项量且所有值加起来等于1
w=A*W;%如果A的矩阵是理想状况的话这里W=w
lam=sum(w./W)/n;%通过这一步最大lam
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45];
CI=(lam-n)/(n-1);
CR=CI/RI(n);%计算误差
if CR<0.10 %如果误差小于0.1则可以接受
disp('此矩阵的一致性可以接受!');
fprintf('Cl=');disp(CI);
fprintf('CR=');disp(CR);
fprintf('W=');disp(W);
else
disp('此矩阵的一致性不可以接受!');
end
对于不同阶判断矩阵是否满足一致性,引入判断矩阵的平均随机一致性指标RI(rand index)。Saaty给出的RI的值是一连串系数,对应各阶矩阵分别
1阶和2阶会提示不满足一致性检验,但只要矩阵斜对称就可以了。因为RI(1)和RI(2)都等于0,导致CR为NaN不能进入if语句。但是可以求出权重比W。
B站视频看到的矩阵数据,但是RI数组和我不一样。我的RI数组是在建模神书司守奎的算法大全上看的。
https://www.bilibili.com/video/av29474522/?p=2