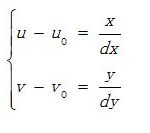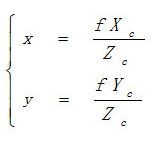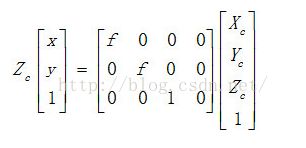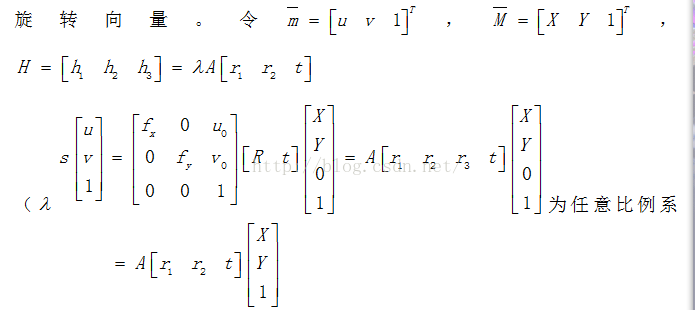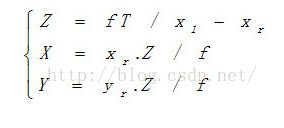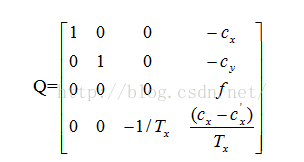双摄像头三维重建
双摄像头三维重建报告
一、摄像机成像模型
1.1 针孔摄像机模型
在此模型中，光线是从很远的物体发射过来，通过一个很小的针孔点（或摄像机镜头），投影到成像表面，其结果是在投影平面图像被聚焦。
如图所示，AO为物距，CO为焦距f，另X为物体长度，x为图像长度，则由三角形相似可得：
1.2改进后的成像模型
此模型使成像为正像，实际上是把投影屏幕放到针孔（摄像头）前面，方便分析，如下：
空间点
由通过投影中心O的光线投影到图像平面上，相应的图像点为p(x,y).在实际摄像机中镜头中心通常不在光轴上，引入两个偏移参数Cx和Cy，可以计算出图像点坐标：
这一投影变换可以用矩阵来表示：q=MQ
其中
，M称为内参数矩阵，另外光学镜头在成像过程中会使图像出现畸变，畸变向量[k1,k2,p1,p2,k3]可以在矫正图像时用来还原图像原型。
为表示物体所在世界坐标系与摄像机坐标系之间的关系，引入旋转矩阵R和平移向量T来。旋转矩阵R表示了两个坐标系相对旋转的角度，平移向量表示了两个坐标系原点的相对偏移量。
1.3摄像机标定与图像矫正
计算三维空间中的物体的位置信息，从而重建、识别出物体是计算机视觉中的一项基本的任务。物体点在空间中的三维位置是通过摄像机的成像模型和物体图像坐标共同决定的，物体点三维位置计算是利用摄像机的内外参数和标记点在图像中的对应位置，来计算出标记点在三维空间中的实际位置。而摄像机的标定是为了获得摄像机的内外参数。
在摄像机标定过程中常用到各种坐标系之间的转换，常用的坐标系如下图所示：
在上图中，摄像机的坐标系XcYcZc，图像坐标系为XO1Y，图像像素坐标系UO2V，世界坐标系XwYwZw。P为三维空间中的一个点，在世界坐标系中坐标为(Xw,Yw,Zw)，在摄像机坐标系中的坐标为(Xc,Yc,Zc)。P与摄像机光心的连线和图像平面会有一个交点，这个交点就是空间点P在图像上的成像位置P，P在图像像素坐标位置为(u,v)，在图像物理坐标的位置为(x,y)，成像平面和摄像机光心的距离即为焦距f。
图像物理坐标系和图像像素坐标系的转化关系：
根据三角形原理得到公式： 
用齐次方程表示上面的公式为：
世界坐标系和摄像头坐标系之间的转化关系为：
其中，R为3*3的旋转矩阵，T为3*1的平移向量。
通过下面公式可以得出图像像素坐标系和世界坐标系之间的关系，这个转换关系是我们最终计算需要的坐标关系。
对于上述公式中的未知参数，我们通过摄像机标定来获得。本文利用张正友标定方法获取摄像机的内外参数，该方法摆脱了传统方法的一些缺点，例如对设备要求高、操作繁琐等，能够比较准确的符合计算机视觉系统的要求。
其中，M(X,Y,0)为标定板上的一点，m(u,v)为图像上与点M对应的像素点，在这里假设模板平面在世界坐标系中的Z=0，则M和m的转化关系如下公式所示：
（4.6）
其中，s为任意比例系数，r1，r2，r3为旋转矩阵在XYZ三个方向上分别得旋转向量。令
（为任意比例系数），则：
旋转矩阵R为正交单位矩阵，利用这一性质可以得到的两个约束关系为：
由于摄像机有五个未知的内参数，而只有两个约束方程，因此至少需要大于等于三幅图像时，才能线性的求出唯一解，即标定出了这些内外参数。
通过摄像机获得多幅棋盘标定板图像，将图像输入到openCV函数cvFindChessboardCorners()中，可得到棋盘上角点图像像素坐标，将图像坐标输入到函数cvCalibrateCamera2()中，可以计算出摄像机内参数矩阵、畸变系数、旋转矩阵和平移向量。得到的这些内外参数可用于以后处理图像，比如旋转矩阵和平移向量可用来计算物体实际坐标位置，内参数矩阵和畸变系数可用来对图像进行矫正。将内参数矩阵和畸变系数输入到函数cvInitUndistortMap()，得到畸变映射，函数cvRemap应用该映射后，对图像进行了矫正。（calibratefang08.cpp）
试验中图像矫正前后对比结果如下：
二、双摄像头立体成像
双摄像头立体成像实际上是在模仿人的双眼成像原理，双摄像头立体成像大体包括四个步骤：消除畸变、摄像机校正、图像匹配、重投影。
2.1物体点三维位置计算
这是一个理想模型，要求两台摄像机的像平面精确位于同一平面上，两个光轴严格平行，摄像机距离一定，焦距相同fr=fl，并且假设主点和已经校准，在左右图像上具有相同的像素坐标。
物理点P，在双目摄像机拍摄的图像上的坐标是不同的，在左摄像机的像平面上横坐标为xl，右摄像机的像平面上横坐标为xr，d = xr – xl为两图像的视差。根据三角形相似原理，可以算出空间点的坐标位置（X,Y,Z）：
2.2极线约束
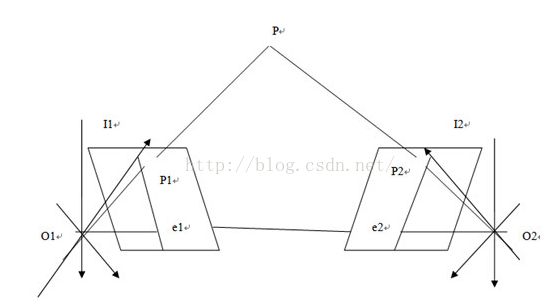
双目视觉原理中存在着一种极线约束的性质，某一个空间点分别在双目摄像机对应的图像上投影，获得其中一个摄像机对应的图像上的点的投影位置，就可以根据极线约束的原理[39]，计算出空间点在另外一个摄像机对应的图像上的投影点所在的一条直线。极线约束原理如图所示：
其中，空间点P，O1和O2分别为两个摄像机的光心，I1和I2分别为两个摄像机所对应的图像，P1和P2为空间点P在两个摄像机对应的图像上的投影点。从上图中可以看出点O1、O2和P确定了一个平面，O1和P的连线和图像I1交于点P1，O2和P的连线和图像I2交于点P2，平面PO1O2和图像I1交于直线e1，平面PO1O2和图像I2交于直线e2。即，知道图像I1上的一点P1和双目摄像机之间的位置关系，就可以得出P1在I2上对应的极线e2，且空间点P 的另外一个投影点P2在直线e2上。
在openCV中要想计算出极线，必须先算出基础矩阵F。基础矩阵包含了物理空间中两个摄像机相关的旋转和平移信息，以及两个摄像机的内参数。基础矩阵是将一台摄像机的像平面上的点在图像坐标系上的坐标和另一台摄像机的向平面上的点关联起来。可以用函数cvFindFundamentalMat()来计算得到基础矩阵，之后可再用函数cvComputeCorrespondEpilines()计算出极线。(calibratefang08.cpp)
2.3立体标定
在立体标定中，两摄像机内参数及畸变系数可单个标定得出，最关键的问题是获得两个摄像机之间的位置关系，双目成像的原理如图所示：
在双目标定的时候，用两个摄像机同时拍摄标定板，对于同一个位置的标定板，左摄像机的旋转矩阵和平移矩阵分别为Rl和Tl，右摄像机的旋转矩阵和平移矩阵分别为Rr和Tr。两个摄像机的空间位置关系表示为：
其中R为正交旋转矩阵，T为平移向量。两个摄像机参数之间的关系表示为：
将单目摄像机标定得到的外参数就可以计算出两个摄像机之间的旋转矩阵和相对平移矢量R和T。
在openCV中可通过函数cvStereoCalibrate（）进行立体标定，得到有用的参数。该函数通过输入角点图像坐标得到正交旋转矩阵、平移向量、基础矩阵、本征矩阵。
2.4摄像机立体校正及匹配
对每个摄像机，我们都会有一个畸变向量、一个旋转矩阵、校正和未校正的摄像机矩阵，用这些向量使用函数cvInitUndistortRectifyMap()创建一个映射，该函数从原始图像插值出一幅新的校正图像。摄像机立体校正的目的是使摄像机在数学上对准及使去除摄像机镜头引起的图像畸变。
之后对于矫正好的图像进行立体匹配：匹配两个不同的摄像机视图，即找出同一个世界物体点在左右成像平面上的坐标位置。此时便成求出该点的视差值：d = xr – xl.由2.1节的知识便可求出该世界物体点的深度值。openCV中可以使用函数cvFindStereoCorrespondenceBM()，通过输入成对的左右图像，来获取视差图disparityImage。
2.5三维重投影
投影矩阵P将齐次坐标中的3D点转换到齐次坐标系下的2D点，即：
如果给定图像坐标和摄像机内参数矩阵，二维点同样可以重投影到三维中，重投影矩阵如下：
其中，Cx是主点在右图像上的x坐标，除该变量外其余均来自左图像。
所以给定一个二维齐次图像坐标点和其关联的视差d,可以将此点投影到三维中：
在openCV中，可通过函数cvStereoRectify()在给出摄像机内外参数后计算出重投影矩阵Q,再将重投影矩阵Q和上面算出的视差图disparityImage输入到函数cvReprojectImageTo3D()中，计算出三维点（X/W,Y/W,Z/W)。Result3DImage深度映射（doublecalibrationfang08.cpp）
三、目前问题
三维重建方面目前进展到此，对于输入的一幅图像，已经可以计算出了这幅图像每一个像素点在世界坐标系中的三维点坐标（X/W,Y/W,Z/W)，其计算结果准确度还有待提高。
对于接下来的四目摄像头重建，目前还没有太多思路，因为双目摄像头标定是在正前方平行摆放固定间距的两个摄像机（模仿人眼立体成像方式），所以四个摄像机若前后左右放置的话，四个摄像机的同时标定及匹配很难做到。