平面----计算机图形学的基础几何知识

平面在数学上的定义是，平面，是指面上任意两点的连线整个落在此面上。

1. 在现实生活中你很容易一眼看出什么平面，但是在计算机的程序里，你将如何表示一个平面的呢？
2. 又是怎么样求点到平面的距离？
3. 判断点在平面的正面还是反面？
4. 线与平面的交点又是怎么求出来的呢？

这篇文章就简单讨论这么几个问题，本文代码有TypeScript所实现，看起来和其他面向对象语言一样，求点积叉积的方法不具体实现，如果有疑惑可以查看我之前的文章。

平面的定义

平面，我们可以通过一条法线和一个点来表示，这个点我们为了方便，就取法线的点， 由于知道法线，所以只有法线单位化，确定这个在法线方向的长度即可。平面方程就用单位长度的法向量和常数表示，在程序上就采用四个浮点数来表示。

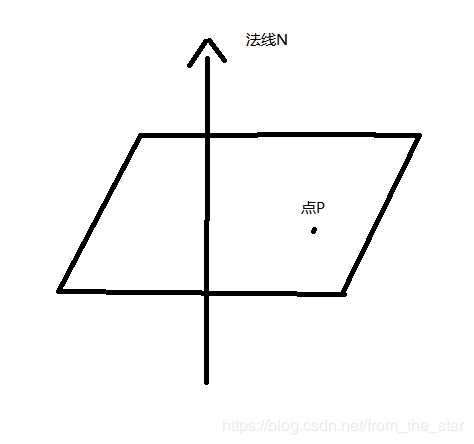
我们都知道三个点（不在一条直线上的三个点）可以确定一个平面。下面代码就是输入三个点输出一个平面的表示。

function planeFromePoints(a:Vector3,b:Vector3,c:Vector3):Vector4{
    //计算三个点构成的法向量
    let normal = Vector3.cross(b-a,c-a).normalize();
    //点a在法线上的投影长度
    let d = Vector3.dot(normal,a);
    let result = new Vector4(normal.x,normal.y,normal.z,d);
    return result;
}

通过法线和一个点构造一个平面的代码更简单，我就不重复了。

点到平面的距离与关系

下面就回答问题2和3，这也是经常会出现在我们编码过程的问题。

先进行单位化平面，因为容易计算点到平面的有向距离。其实之前我们的函数已经单位化平面了，平面中的法向量为单位向量，n那么这个向量就称为单位化平面。

然后我们就可以利用如下代码极端三维空间中任意一个点与平面的有向距离：

function planeDistanceFromPoint(plane:Vector4, point:Vector3){
    return (point.x*plane.x + point.y*plane.y + point.z*plane.z - plane.w);
}

最后，如果要判断一个点是在平面的正面、反面还是平面上，只要判断有向距离即可：
大于0是正面；
等于0是平面上；
小于0是反面。

线段与平面的关系

线段由起点和终点两个点决定，只要起点和终点到平面的有向距离，一个为正一个为负，就代表线段与平面相交，否则不相交。

射线与平面的交点

最后一个问题也很常见，在光线追踪里就可以碰到。

射线的表示方式为，一个方向单位向量D，还有一个起点O（式1）

$$p=O+t\cdot D(t\in (0,\infty ))$$

如果是直线线放开一下t的取值范围即可。

求射线的与平面的交点：

1. 首先求出射线起点到平面的距离t，这个距离没有方向
2. t乘以方向向量，得到起点到交点的向量，在加上起点坐标，就是交点的坐标了

	function RayIntersectPlane ( plane:Vector4, origin:Vector3, direction:Vector3 ) {
        const denominator = plane.normal.dot( direction );
		const t = -planeDistanceFromPoint( plane, origin)/denominator;
        // denominator为正：代表射线与平面的法向量为同一方向
        // 平面与起点的有向距离为正：代表起点在平面的正面
        // 这样意味着射线在平面一侧
        // 所以 t<0 代表 射线与平面没有交点
		if ( t < 0 ) {
			return null;
		}
		let target = new Vector3();
		target.copy( direction ).multiplyScalar( t ).add( origin );
		return target;

	}

更多的信息大家可以去查看threejs数学库中的Plane类。