浅谈 拓扑排序

我发现我好喜欢浅谈（逃

基本概念

对一个有向无环图 $DAG$ $(DirectedAcyclicGraph)$ 进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点 $u$ 和 $v$，若边 $<u,v>\in E(G)$，则 $u$ 在线性序列中出现在 $v$ 之前。通常，这样的线性序列称为满足拓扑次序 $(TopologicalOrder)$ 的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

实话说我没看懂，我们可以换一种更加通俗的说法。假设一个 $DAG$，如下。

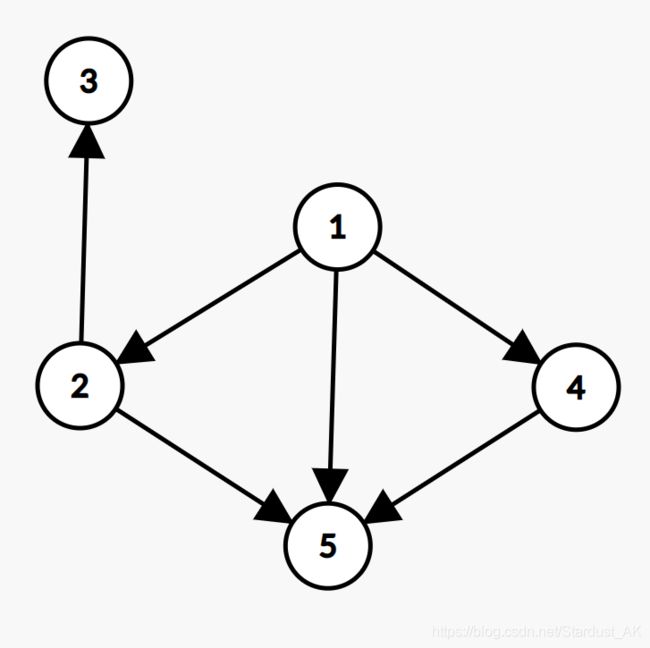
然后你可以把它看成某个鬼杀士的学习任务表：
任务1：掌握全集中呼吸方式。
任务2：掌握由全集中呼吸衍生出的日之呼吸。
任务3：掌握日之呼吸十三式。
任务4：掌握某些由全集中呼吸衍生出的普通刀法。
任务5：让刀法与日之呼吸相结合，开创火之神神乐。

哈！你哪怕没看过鬼灭安利，你也能大概分辨出完成任务2需要先完成任务1，完成任务3需要先完成任务2，完成任务4需要先完成任务1，完成任务5需要先完成任务2和任务4。

这样看来，上图的 $DAG$ 其实就是描述了5个任务的完成先后关系。而拓扑排序的用处就是让我们求出一个完成任务的先后顺序。这个顺序一定满足：完成当前任务时，它所需要完成的前置任务一定都被完成了。而我们称这样的顺序为拓扑序，显然每个 $DAG$ 的拓扑序可能不止一种。

上图的其中一种拓扑序为：1，2，4，3，5。

你会发现，这是不是很像 $BFS$ 序！其实拓扑排序的算法思路就和 $BFS$ 有点像。

算法思路

我们依然以那个学习任务表为例。在什么情况下当前任务才可以完成？当它的前置任务都完成时即可。放到 $DAG$ 中，如果一个点能被“完成”，则代表所有有边指向它的点都被完成了。那如果我们每完成一个点就删除所有以它为起点的边，你会发现，下一次能被完成的点入度一定为0！

所以我们可以直接使用这个算法思路进行实现。首先找到一开始入度为0的点，将它加入拓扑序。删除以他为起点的所有边（相当于 $BFS$ 中得到一个点就向四周拓展的思路。然后在不在拓扑序中的点中找到下一个入度为0的点，然后……直到所有的点都加入拓扑序，则现在的拓扑序就是我们要求的顺序。

而如果有一次找不到入度为0的点了怎么办？那就是有环了！因为在删除了所有除环以外的点后，环上的每一个点的入度一定恒为1。你就再也找不到入度为0的点了。可以看看下图。删除4后会发生什么/xyx

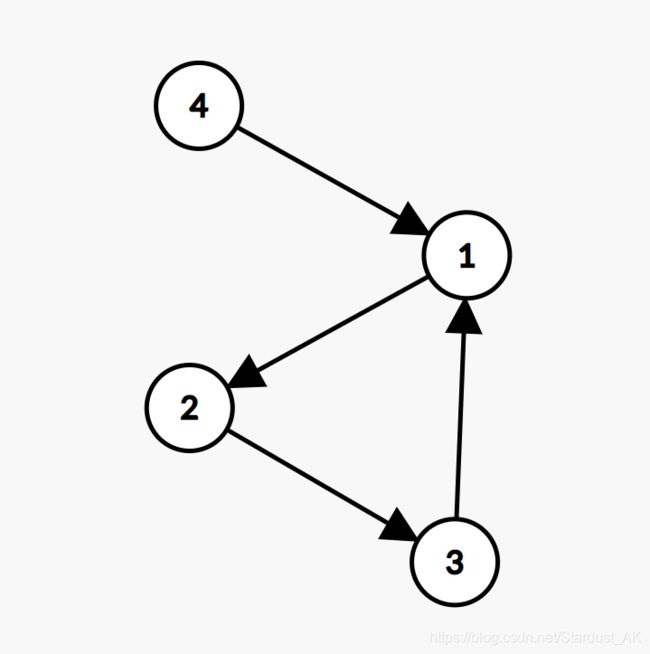
于是乎……

具体实现

#include 
#include 
using namespace std;

const int MAXN = 10005;
vector<int> DAG[MAXN]; // 有向无环图，邻接表
void Add_Edge(int u, int v) {
	DAG[u].push_back(v); // 存边
}
int In_Degree[MAXN];
// 保存每个点的入度
bool vis[MAXN];
// 记录当前点是否在拓扑序中
int Topological_Order[MAXN], len_TPO = 0;
// 保存拓扑序及拓扑序长度
int n, m;
// n个点，m条边
bool flag = false;
// 判环

void Topological_Sort() {
	for(int i = 1; i <= n; i++) {
		int index = -1;
		for(int j = 1; j <= n; j++) {
			if(!vis[j] && In_Degree[j] == 0) {
				// 未在拓扑序中，而入度为0
				index = j;
				break;
			}
		}
		if(index == -1) { // 没有找到，表示有环
			flag = true;
			return ;
		}
		vis[index] = true; // 加入拓扑序
		Topological_Order[++len_TPO] = index;
		for(int j = 0; j < DAG[index].size(); j++) {
			int end = DAG[index][j];
			In_Degree[end]--;
			// 以index为起点的边的终点的入度减一
		}
	}
}

int main() {
	scanf ("%d %d", &n, &m);
	for(int i = 1; i <= m; i++) {
		int u, v;
		// 起点为u，终点为v的边
		scanf ("%d %d", &u, &v);
		Add_Edge(u, v);
		In_Degree[v]++; // 入度加一
	}
	Topological_Sort();
	if(!flag) {
		for(int i = 1; i <= len_TPO; i++)
			printf("%d ", Topological_Order[i]);
	}
	else
		printf("No solution");
	return 0;
}

多么美丽的代码~（逃

不过上面 $O(n^2)$ 代码是可以优化的，我们可以将所有的已知的入度为0的点放进队列。然后直接在队列里操作就行了，不用每次都遍历。话说，上面的代码长得像不像Dijkstra

优化

#include 
#include 
#include 
using namespace std;

const int MAXN = 10005;
vector<int> DAG[MAXN]; // 有向无环图，邻接表 
void Add_Edge(int u, int v) { 
	DAG[u].push_back(v); // 存边 
}
int In_Degree[MAXN]; 
// 保存每个点的入度
int Topological_Order[MAXN], len_TPO = 0;
// 保存拓扑序及拓扑序长度 
int n, m; 
// n个点，m条边 
bool flag = false; 
// 判环 
queue<int> q; 
// 记录入度为0的点 

void Topological_Sort() {
	for(int i = 1; i <= n; i++)
		if(In_Degree[i] == 0) // 入队 
			q.push(i); 
	while(!q.empty()) {
		int index = q.front(); // 取出队头
		q.pop();
		Topological_Order[++len_TPO] = index; 
		// 放入拓扑序 
		for(int i = 0; i < DAG[index].size(); i++) {
			int end = DAG[index][i];  
			In_Degree[end]--; // 更新相连边的终点入度 
			if(In_Degree[end] == 0)
				q.push(end) // 入队 
		} 
	}
	if(len_TPO != n) {
		// 队列为空，但还有点未进入拓扑序，说明有环
		flag = true;
		return ; 
	}
}

int main() {
	scanf ("%d %d", &n, &m);
	for(int i = 1; i <= m; i++) {
		int u, v; 
		// 起点为u，终点为v的边
		scanf ("%d %d", &u, &v);
		Add_Edge(u, v);
		In_Degree[v]++; // 入度加一 
	} 
	Topological_Sort();
	if(!flag) {
		for(int i = 1; i <= len_TPO; i++)
			printf("%d ", Topological_Order[i]);		
	}
	else 
		printf("No solution");
	return 0;
} 

其实你会发现，两个代码得出的拓扑序是不一样的，但经过验证发现都是对的，这也再次说明了拓扑序不具有唯一性。

完结撒花~ 把义忍给爷锁死