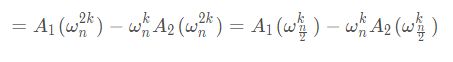快速傅里叶变换(FFT)
FFT,是用来在O(nlogn)时间复杂度内解决关于单一元素的多项式*多项式问题的算法。
众所周知,一个关于x的n项式可以表示为a[0]+a[1]*x+a[2]*x^2+...+a[n-1]*x^(n-1),这就是系数表示法。
我们考虑另一种表示方法,对于一个上述形式的n项式,我们只要知道n组不同的x,和将这n组x代入n项式后得到的值(我们设其为f(x)),就可以唯一确定这个n项式。用这样的n组(x,f(x))表示一个n项式就是点值表示法。
当两个多项式相乘时,如果是用系数表示法,那么时间复杂度不可避免是O(n^2),但如果这两个多项式是用点值表示法表示的,且所选的x的集合都相同,那么我们的新多项式用点值表示法即为n组(x,f1(x)*f2(x))。
但是!日常生活中我们正常是不会用点值表示法来表示多项式的,所以FFT就是用来将一个多项式的系数表示法转化为点值表示法的算法。而IFFT(快速傅里叶逆变化)就是用来将多项式从点值表示法转化为系数表示法的算法。
关于这n组不同的x到底怎么选,快速傅里叶变换是有规定的选值的。
对于一个n项式,令复数w(n,k)=cos(2*pi*k/n)+sin(2*pi*k/n)i。(其中0≤k≤n-1,pi为3.1415926535....,2*pi=360°)。xk=w(n,k)共n组。
这是从代数意义来看的(其实可以直接背),从几何意义来看,w(n,k)都在复数平面以原点为圆心半径为1的圆上。且是将这个圆n等分,w(n,0)=1+0i, k以逆时针递增取点。 然后根据三角函数乱搞一波就可以知道上述代数式。
但我们知道一个x,求f(x)还是要n的时间。怎么办呢?
copy自https://blog.csdn.net/enjoy_pascal/article/details/81478582#commentBox 多谢WD大佬!
好了,FFT搞完了。
接下来看IFFT,有这样一个结论:一个多项式在分治的过程中乘上单位根的共轭复数,分治完的每一项除以n nn即为原多项式的每一项系数。意思就是说这个可以一样用FFT的函数做。具体看模板吧。不太会描述的说。
值得注意的是,当给一个n项多项式,一个m项多项式,应令N=n+m-1,并将N调整为一个更大的2次幂数。
然后fft(a,N,1); fft(b,N,1);
ai*=b[i]
fft(a,N,-1)
模板(我只会递归的:
#include
#include
using namespace std;
#include
#define cp complex
#include
#define pi 3.1415926535
cp a[3000010],b[3000010];
void fft(cp *a,int n,int bz) //这里的bz表示现在是点转系还是系转点
{
if (n==1) return;
int mid=n/2;
cp b[n+10];
for (int i=0;i<=mid-1;i++) b[i]=a[i*2],b[i+mid]=a[i*2+1];//这里a,b还是系数
for (int i=0;i<=n-1;i++) a[i]=b[i]; //将b分为基数和偶数部分
fft(a,n/2,bz); fft(a+mid,n/2,bz);//递归求出A1,A2
for (int i=0;i<=mid-1;i++)
{
cp t(cos(2*pi*i/n),bz*sin(2*pi*i/n)); //t=w(n,i)
b[i]=a[i]+t*a[i+mid]; b[i+mid]=a[i]-t*a[i+mid];
}
for (int i=0;i<=n-1;i++) a[i]=b[i];//a已经变成点值了
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
int t=n+m+1;
for (int i=0;i<=n;i++) scanf("%lf",&a[i].real());
for (int i=0;i<=m;i++) scanf("%lf",&b[i].real());
for (n=1;n
for (int i=0;i<=n-1;i++) a[i]=a[i]*b[i];//点值相乘
fft(a,n,-1);//点转系
for (int i=0;i<=t-1;i++) printf("%d ",int(a[i].real()/n+0.5));//要/n后四舍五入才是真正的系数
return 0;
}