最小生成树算法：普利姆、克鲁斯卡尔（附详细代码）
【注：】本文代码在c++环境下运行
普利姆算法和克鲁斯卡尔算法，都可以用于最小生成树的寻找。
初学两种算法，很容易混淆，经常会把普利姆的算法过程记到了克鲁斯卡尔的头上。这是因为这两个算法都是以人名命名，难以记忆。所以，我建议，根据两算法的特点，把克鲁斯卡尔算法记作 “加边算法” 。把普利姆算法记作 “加点算法”。
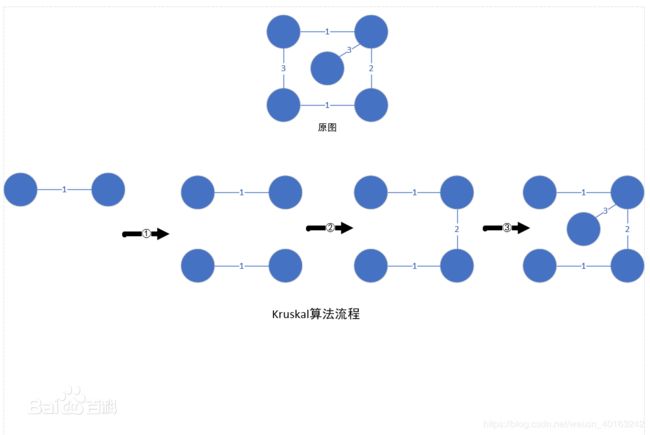
我们今天的算法分析，就以下面这个无向带权图为例子：
其邻接矩阵我们可以画出，如下图：
加边算法克鲁斯卡尔
就是每次选择权值最小的边加入到最小生成树集合中。当然，要满足一个前提，这条边加入进来之后，不能产生回路。
要解决的核心问题就是：1.排序；2.判断一条边的加入，会不会构成环。
核心代码：（详细代码见帖子最后）
//克鲁斯卡尔算法
void kruskal(EData **edges, PGraph G) {
int k = 0; //对应结果集的指针
EData res[MAX]; //存最小生成树结果的边
sort(edges, G); //对边的权值排序
//遍历每一条边
for(int i = 0;i < G->edgnum;i++){
//把每一条边的两个结点编号拿出来
int p_start = get_index((*edges + i)->start);
int p_end = get_index((*edges + i)->end);
//p_start和 p_end 如果不属于同一个集合才能加入。否则加入他们就会产生回路。
if(G->vexs[p_start] != G->vexs[p_end]){
res[k++] = *(*edges + i);
//要把所有连通分量编号为 p_end的节点给置为p_start。这一步是至关重要的一步！！
for(int j = 0;j < G->vexnum;j++){
if(G->vexs[j] == G->vexs[p_end]){
G->vexs[j] = G->vexs[p_start];
}
}
}
}
cout << "克鲁斯卡尔算法生成的最小生成树的各边为：" << endl;
for(int i = 0;i < k;i++){
cout << res[i].start << ", " << res[i].end << "权值为：" << res[i].weight << endl;
}
}
加点算法普利姆：
设定一个U集合，起始阶段把源点加入U集合内部，
每次把离 U集合 最近的那个结点加入U集合内，然后更新U集合到U集合外其他各点的距离，更新的过程我们称为 松弛。
再说大白话一点，每次把权值最小的外部结点加入U集合内。等所有结点都加入进U集合了，算法终止，最小生成树也成了。
核心代码：（完整代码见帖子最后）
//普利姆算法
int* prim(PGraph G, int *sum) {
int* res = (int*)malloc(sizeof(EData) * G->vexnum);int k = 1;*sum = 0; //res数组装每次选择加入最小生成树的结点序号
*res = 0; //第一个节点作为初始节点
for(int i = 0;i < G->vexnum;i++){ //初始化dis数组 和 src数组
G->dis[i] = G->matrix[0][i];
G->src[i] = 0;
}
for(int i = 0;i < G->vexnum;i++){
int min = MAX_INT, min_index = 0;
//每次找出dis数组中的最小值，作为下一个节点
for(int j = 0;j < G->vexnum;j++){
if(G->dis[j] != 0 && G->dis[j] < min){
min = G->dis[j];
min_index = j;
}
}
//结果更新
*sum = *sum + G->dis[min_index];
G->dis[min_index] = 0; //min_index结点就进入U集合了
*(res + k) = min_index;
k++;
//dis数组更新。根据这个最小值节点，松弛附近的权值
for(int j = 0;j < G->vexnum;j++){
//考虑到负权值的情况
if(G->matrix[min_index][j] < G->dis[j] && G->dis[j] != 0){
G->dis[j] = G->matrix[min_index][j];
G->src[j] = min_index; //要更改路径
}
}
}
return res;
}
下面是完整可运行代码，包含所有数据结构及方法：
克鲁斯卡尔的：
#include运行效果：
普利姆的：
#include运行效果：
