【2020年杭电暑假第五场】6814 Tetrahedron

题目链接： http://acm.hdu.edu.cn/showproblem.php?pid=6814

Generate three integers a, b, and c in [1,n] with equal probability independently, and use them as the three right-angle side length of a right-angled tetrahedron. Find the expectation of the reciprocal square of the distance from the right-angle apex to the slope (Euclidean distance).

For each test case, output a line containing the answer mod 998244353.

Input
In the first line, you should read an integer T denoting the number of test cases.

In every test case, the only line will include an integer n.

It is guaranteed that T is no larger than 2×106 and n is no larger than 6×106.

Output
For each test case, output the only line containing just one integer denoting the answer mod 998244353.

Sample Input
3
1
2
3

Sample Output
3
124780546
194103070

题意

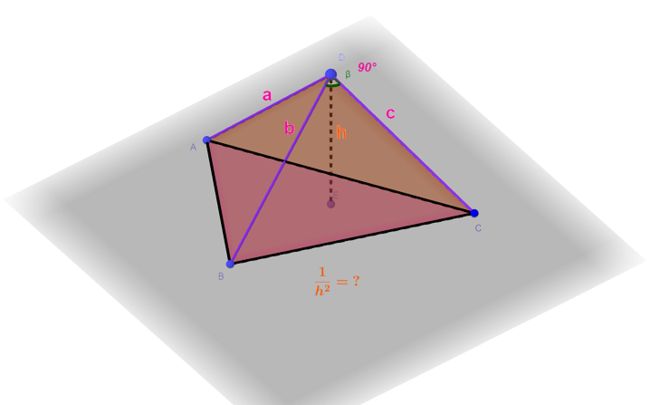
给定n，在[1,n]中等概率随机选出3个数$a,b,c$，做直角四面体（$a,b,c$三遍两两垂直），记顶点到底面的距离为$h$,求数学期望$E(\frac{1}{h^2})$

思路

设$a,b,c$为空间直角坐标系的三条坐标轴， 直角四面体的顶点作为坐标系的原点，直角四面体的底在坐标系的平面方程为$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$，那么$h$为原点到该平面方程的直线距离。

$$h=\frac{1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}}$$
$$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$$

然后$a,b,c$在$[1,n]$间等概率选取某个数，所有数字出现的次数都是$n$次，所以$\frac{1}{a^2},\frac{1}{b^2},\frac{1}{c^2}$都为[1,n]种的某个$\frac{1}{i^2}$。

最后求数学期望，每个$a,b,c$都有$n$种选法，所以一共有$n^3$种，对于每个a，都有$n^2$个。
$$E(\frac{1}{h^2})=\frac{n^2\ast 3\ast {\sum }_{i=1}^n\frac{1}{i^2}}{n^3}(n\ge 3)$$
$$E(\frac{1}{h^2})=\frac{3\ast {\sum }_{i=1}^n\frac{1}{i^2}}{n}(n\ge 3)$$

所以只要预处理一下，直接$O(1)$得出答案。

Code

#include 

using namespace std;

typedef long long ll;
typedef long double ld;
typedef pair<int, int> pdd;

#define INF 0x7f7f7f
#define mem(a, b) memset(a , b , sizeof(a))
#define FOR(i, x, n) for(int i = x;i <= n; i++)

// const ll mod = 1e9 + 7;
// const int maxn = 1e5 + 10;
// const double eps = 1e-6;

const ll mod = 998244353;

ll quick_pow(ll a, ll b)
{
    ll ans = 1, base = a;
    while(b != 0)
    {
        if(b & 1)
        {
            ans = ans * base % mod;
        }
        base = base * base % mod;
        b >>= 1;
    }
    return ans;
}

ll inv[6000005];
ll f[6000005];

void Init()
{
    inv[1] = 1;
    for(int i = 2;i <= 6000002; i++) {
        inv[i] = mod - (mod / i) * inv[mod % i] % mod;
    }
}

void solve() {
    Init();
    for(int i = 1;i <= 6000002; i++) {
        f[i] = (f[i - 1] + (inv[i] * inv[i]) % mod) % mod;
    }
    int T;
    scanf("%d",&T);
    while(T--) {
        ll n;
        scanf("%d",&n);
        ll k = 3 * f[n] % mod * inv[n] % mod;
        printf("%lld\n",k);
    }
}


signed main() {
    ios_base::sync_with_stdio(false);
    //cin.tie(nullptr);
    //cout.tie(nullptr);
#ifdef FZT_ACM_LOCAL
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
    signed test_index_for_debug = 1;
    char acm_local_for_debug = 0;
    do {
        if (acm_local_for_debug == '$') exit(0);
        if (test_index_for_debug > 20)
            throw runtime_error("Check the stdin!!!");
        auto start_clock_for_debug = clock();
        solve();
        auto end_clock_for_debug = clock();
        cout << "Test " << test_index_for_debug << " successful" << endl;
        cerr << "Test " << test_index_for_debug++ << " Run Time: "
             << double(end_clock_for_debug - start_clock_for_debug) / CLOCKS_PER_SEC << "s" << endl;
        cout << "--------------------------------------------------" << endl;
    } while (cin >> acm_local_for_debug && cin.putback(acm_local_for_debug));
#else
    solve();
#endif
    return 0;
}

赛后又交了已发，发现T了，赛中AC，赛后T了，很迷，最后把cin改成scanf还是对了，差点吓死我。