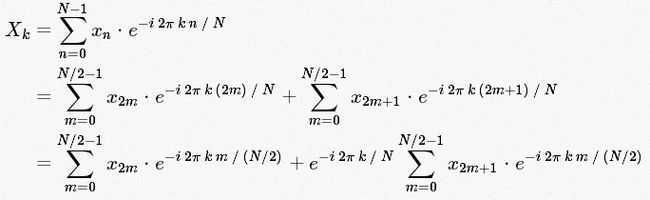【数学】快速傅里叶变换(FFT)
这几天简单学习了 FFT 算法,在此做一个小的总结。
要解决的问题
FFT算法可以用来解决这样一类问题。
设有多项式:
求多项式 C(x)=A(x)⋅B(x) 。
n2 的方法
很容易想到该问题的 O(n2) 解法,这里不做解释:
void Calc(double* a, double* b, double* c, int n) {
/*
A(x) = a[0] + a[1]*x + a[2]*(x^2) + a[3]*(x^3) + ... + a[n-1]*(x^(n-1))
B(x) = b[0] + b[1]*x + b[2]*(x^2) + b[3]*(x^3) + ... + b[n-1]*(x^(n-1))
C(x) = c[0] + c[1]*x + c[2]*(x^2) + c[3]*(x^3) + ... + c[2n-2]*(x^(2n-2))
*/
for(int i=0; i<2*n; i++) c[i] = 0;
for(int i=0; ifor(int j=0; j 优化到 nlogn
1、多项式的两种表示方法
我们熟知的是多项式的系数表示法,通过给定一组 {a0,a1,...,an−1} 来确定一个唯一的多项式:
而多项式还可以有另一种表示法,称为点值表示法:
其中 yi=A(xi) ;
可以证明,对一组互不相同的 {x0,x1,...,xn−1} ,该方法也可以唯一地表示一个多项式。
为什么要引入点值表示法这个并不“直观”的形式呢?下表显示了它的好处:
| 执行运算 | 系数表示 | 点值表示 |
|---|---|---|
| A(x)+B(x) | O(n) | O(n) |
| A(x)∗B(x) | O(n2) | O(n) |
*当然,点值表示法下的运算均要求 A(x) 和 B(x) 所取的点集 {x0,x1,...,xn−1} 是相同的,且运算出的 C(x) 也为点值表示法。
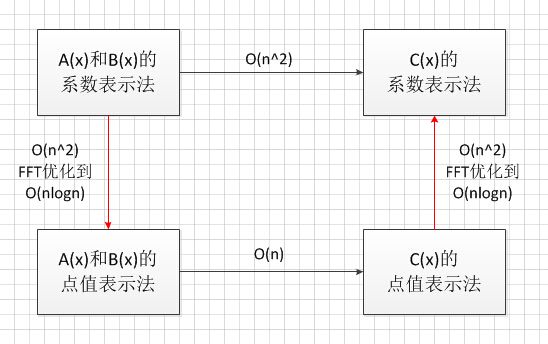
2、改变求解路线降低复杂度
我们的目的是从 A(x) 和 B(x) 的系数表示法求解出 C(x) 的系数表示法,显然直接求解复杂度是 O(n2) 的。
然而我们了解点值表示法后,知道了在点值表示法下计算 C(x) 的复杂度仅需 O(n) ,那么我们能否利用这一性质降低复杂度呢?
然而经过观察发现,将 A(n) 从系数表示转化到点值表示的复杂度是 O(n2) 的。。。这里也是瓶颈所在,只要这里能优化,我们就能得到整体更优的算法。
幸运的是,这里确实是可优化的,快速傅里叶变换(FFT)算法将其复杂度降至 O(nlogn) ,至于优化的原理,将在简单介绍傅里叶变换之后再说明。
3、傅里叶变换及其快速算法
傅里叶变换是电子类学科的基础知识,在许多工科领域里有着重要应用。可惜我们当年学高数的时候直接把这节跳过了。。。
关于傅里叶变换的介绍,可以参考:链接地址1 和 链接地址2
我们这里不讨论连续傅里叶变换。离散的傅里叶变换公式如下( i 为虚数符号):
可以发现正逆变换是类似的,简单起见,我们只看正变换。DFT变换暴力求解也需要 O(N2) 的时间,然而观察下面的做法:
可以发现,通过奇偶分开,一个问题被分成了两个规模减半的相同问题。如此递归下去,即可在 O(nlogn) 的时间内完成运算。
4、用FFT优化转换过程
从上面的介绍中,我们已经知道了快速傅里叶变换的算法,那么如何利用该算法优化“系数表示法到点值表示法”这一转换过程呢?
我们可以考虑转变的过程。显而易见的方法是找 n 个互不相同的 x 值,得到分别对应的 y 值。一般而言,找们找 n 个 x 需要 O(n) 的复杂度,而对每个 x ,又要进到多项式 A(x) 里求一遍和,得到结果又需要 O(n) ,因此总体是 O(n2) 。
这里能做文章的地方就是 n 个 x 值的选取,我们可以按习惯选取 {0,1,2...,n−1} 这样的序列,然而用它的话就无法再优化了 。注意,这里的 x 序列不一定是整数,它甚至可以不是实数。联系上面提到的FFT算法,我们可以取序列 {ω0n,ω1n,ω2n,...,ωn−1n,} ,其中 ωn=e2πi/n 。
再定义 yk=A(ωkn) 。
之后即可利用上面讲到的FFT算法,在 O(nlogn) 的时间内完成运算。
此方法的优点是显而易见的,但缺点是引入了浮点运算,可能会产生精度问题,使用时要保留足够的精度。
FFT 实现代码如下(模板来自kuangbin的这篇博客):
/** 快速傅里叶变换 */
class FFT {
Complex u, t;
void change(Complex arr[], int len) { /// len必须是2的幂
for(int i=1, j=len>>1, k; i1; i++) {
if(i < j) swap(arr[i], arr[j]);
k = len >> 1;
while(j >= k) {
j -= k;
k >>= 1;
}
if(j < k) j += k;
}
}
public:
void fft(Complex y[], int len, int on){ /// on=1是DFT on=-1是IDFT
change(y, len);
double tmp = -on * 2 * acos(-1.0);
for(int h=2; h<=len; h<<=1){
Complex wn(cos(tmp/h), sin(tmp/h));
for(int j=0; j1,0);
int h2 = h >> 1;
for(int k=j; kif(on == -1){
for(int i=0; i 它依赖复数类:
/** 复数类 */
struct Complex {
double x,y; /// 实部,虚部 x+yi
Complex(double _x = 0, double _y = 0): x(_x), y(_y) {}
friend Complex operator +(const Complex &a,const Complex &b) {
return Complex(a.x+b.x, a.y+b.y);
}
friend Complex operator -(const Complex &a,const Complex &b) {
return Complex(a.x-b.x, a.y-b.y);
}
friend Complex operator *(const Complex &a,const Complex &b) {
return Complex(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x);
}
};在算法题目中的应用
注:以下题目代码均省略粘模板的部分,用“ ... ”代替。
1、HDU1402
位数较大的A*B,属于比较裸的FFT,直接按要求操作即可,注意len要补足到2的幂。
#include 1]-'0',0);
}
for(int i=la; i0,0);
}
for(int i=0; i1]-'0',0);
}
for(int i=lb; i0,0);
}
g.fft(x1, len, 1);
g.fft(x2, len, 1);
for(int i=0; i1);
for(int i=0; iint)(x1[i].x + 0.5);
}
for(int i=0; i1] += sum[i] / 10;
sum[i] %= 10;
}
int s = len - 1;
while(sum[s]==0 && s) s--;
for(int i=s; i>=0; i--){
printf("%d", sum[i]);
}
cout << endl;
}
return 0;
}
2、UVALive6886
这个题目要稍微做一点建模,不过也很容易。题意是给出每步可以跳的距离,问在两步之内可以到达的位置(两步跳动的方向一致)。我们建模的话就可以将多项式的某项 aixi 理解成可否跳到位置 i 处, ai=1 表示可以, ai=0 表示不可以,再将两个相同的多项式相乘即可得出两步之内可以到达的位置分布。
#include scanf("%d", &k[i]);
ma = max(ma, k[i]);
}
scanf("%d", &m);
for(int i=0; iscanf("%d", &d[i]);
}
int len = 1;
while(len < 2*ma) len <<= 1;
memset(can, 0, sizeof can);
for(int i=0; i<4*MAXN; i++){
a[i] = b[i] = Complex(0,0);
}
for(int i=0; i1,0);
b[k[i]] = Complex(1,0);
}
g.fft(a, len, 1);
g.fft(b, len, 1);
for(int i=0; i1);
for(int i=0; iint)(a[i].x+0.5);
}
//cout << len << endl; //16
//cout << ma << endl; //5
//for(int i=0; i
//if(can[i]) printf("*%d\n", i);
//printf("*a[%d].x = %.2f\n", i, a[i].x);
//}
int ans = 0;
for(int i=0; iif (can[d[i]]) ans++;
}
printf("%d\n", ans);
}
return 0;
}
/**
3
1 3 5
6
2 4 5 7 8 9
*/ 3、HDU4609
给出一堆木棍的长度,从中挑出三根,求能组成三角形的概率。
建模跟上一题类似,其每一项 aixi 表示长度为 i 的木棍有 ai 根,相乘得到的 aixi 表示两根木棍长度和为 i 有 ai 种取法。当然这里要做一些处理,比如同一根木棍取两次的情况,还有有序取变无序取需要除2。之后统计出前缀和,枚举第三根木棍,并假设它是最长的,就能保证不重不漏。为了保证第三根是最长的,这里要再做一些处理,很容易就能完成。最后用合法方法数除以 C(n,3) 即为概率。
#include scanf("%d", &a[i]);
num[a[i]]++;
}
sort(a, a+n);
int ma = 2 * (a[n-1] + 1);
int len = 1;
while(len < ma) len <<= 1;
for(int i=0; i0);
for(int i=ma; i0, 0);
g.fft(x1, len, 1);
for(int i=0; i1);
for(int i=0; i0.5);
len = 2 * a[n-1];
for(int i=0; ifor(int i=1; i<=len; i++){
num[i] /= 2;
}
sum[0] = 0;
for(int i=1; i<=len; i++) sum[i] = sum[i-1] + num[i];
LL cnt = 0;
for(int i=0; i1-i)*i;
cnt -= (n-1);
cnt -= (LL)(n-i-1)*(n-i-2)/2;
}
LL tot = (LL)n*(n-1)*(n-2)/6;
printf("%.7f\n",1.0*cnt/tot);
}
return 0;
}
这里还有一些待做的题目,做完再把题解加上,to be update…
【附录】参考资料:
[1] http://blog.jobbole.com/58246/
[2] http://blog.163.com/tianyake@yeah/blog/static/749331412010979109623/
[3] 百度百科-快速傅里叶变换
[4] 算法导论(第二版)第30章 多项式与快速傅里叶变换