HDU 2016年中国大学生程序设计竞赛(合肥)-重现赛(感谢安徽大学)
HDU 5969最大的位或
最大的位或
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 274 Accepted Submission(s): 146
Problem Description
B君和G君聊天的时候想到了如下的问题。
给定自然数l和r ,选取2个整数x,y满足l <= x <= y <= r ,使得x|y最大。
其中|表示按位或,即C、 C++、 Java中的|运算。
Input
包含至多10001组测试数据。
第一行有一个正整数,表示数据的组数。
接下来每一行表示一组数据,包含两个整数l,r。
保证 0 <= l <= r <= 1018。
Output
对于每组数据输出一行,表示最大的位或。
Sample Input
Sample Output
思路:给l的二进制补1,只要没超过r就一直补,最后得到的数和r或运算就是结果。
#include
using namespace std;
#define ll long long int
int main()
{
ll l,r;
int T;
scanf("%d", &T);
while(T--){
scanf("%I64d %I64d", &l, &r);
ll tmp = 0, n = 0, s = 1, k = l;
while((k|(tmp+(s< HDU 5968异或密码
|
|
异或密码
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 297 Accepted Submission(s): 113
Problem Description
晨晨在纸上写了一个长度为N的非负整数序列{
ai}。对于这个序列的一个连续子序列{
al,al+1,…,ar}晨晨可以求出其中所有数异或的结果
alxoral+1xor...xorar其 中xor表示位异或运算,对应C、C++、 Java等语言中的^运算。
小璐提出了M个询问,每个询问用一个整数 xi描述。 对于每个询问,晨晨需要找到序列{ ai}的所有连续子序列,求出每个子序列异或的结果,找到所有的结果中与 xi之差的绝对值最小的一个,并告诉小璐相应子序列的长度。 若有多个满足条件的连续子序列,则告诉小璐这些子序列中最长的长度。
Input
包含多组测试数据,第一行一个正整数T,表示数据组数。
每组数据共两行。 第一行包含N+1个非负整数。其中第一个数为N,表示序列的长度;接下来N 个数,依次描述序列{ ai}中的每个数。 第二行包含M+1个整数。其中第一个数为M,表示询问的个数;接下来M个数 xi,每个数对应题目描述中的一个询问。 保证 1 <= N <= 100,1 <= M <= 100, ai <= 1024,| xi| <= 1024,数据组数 <= 100。
Output
对于每组数据输出M + 1行。前M行对应晨晨M个询问的回答,第M + 1行为空行
Sample Input
2 2 1 1 2 0 2 3 1 2 4 3 10 5 1
Sample Output
2 1 3 2 1
|
思路:暴力出子序列,用结构体保存它的异或和 和 长度,排序,按异或和升序排,异或和相同的按长度降序排。二分查找和x最接近的数,用这个数和它左边一个和右边一个来
更新结果,注意左边可能有多个相同的值,由于排序的原因,左边如果有多个相同的值就要取最左,右边就直接取第一个。
#include
using namespace std;
#define inf 1<<30
int a[105], pre[105], ans[105];
int x, res;
struct region{
int l, r, val;
dis(){return r-l+1;}
}rom[10010];
bool cmp(const region a, const region b){
if(a.val==b.val) return (a.r-a.l+1)>(b.r-b.l+1);
return a.val=x){
R = mid-1;
}else L = mid+1;
}//printf("--%d %d %d\n", L, R, mid);
tp = mid;
res = inf;
int tmp;
if(tp>=1){//求左边
tmp = rom[tp-1].val;
while(rom[tp-1].val==tmp&&tp-1>=0)tp--;
if(abs(rom[tp].val-x) HDU5961 传递
传递
Time Limit: 12000/6000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 354 Accepted Submission(s): 160
Problem Description
我们称一个有向图G是传递的,当且仅当对任意三个不同的顶点a,,若G中有 一条边从a到b且有一条边从b到c ,则G中同样有一条边从a到c。
我们称图G是一个竞赛图,当且仅当它是一个有向图且它的基图是完全图。换句 话说,将完全图每条边定向将得到一个竞赛图。
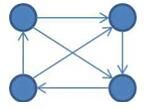
下图展示的是一个有4个顶点的竞赛图。
现在,给你两个有向图P = (V, Ep)和Q = (V, Ee),满足:
1. EP与 Ee没有公共边;
2. (V, Ep⋃Ee)是一个竞赛图。
你的任务是:判定是否P,Q同时为传递的。
Input
包含至多20组测试数据。
第一行有一个正整数,表示数据的组数。
对于每组数据,第一行有一个正整数n。接下来n行,每行为连续的n个字符,每 个字符只可能是’-’,’P’,’Q’中的一种。
∙如果第i行的第j个字符为’P’,表示有向图P中有一条边从i到j;
∙如果第i行的第j个字符为’Q’,表示有向图Q中有一条边从i到j;
∙否则表示两个图中均没有边从i到j。
保证1 <= n <= 2016,一个测试点中的多组数据中的n的和不超过16000。保证输入的图一定满足给出的限制条件。
Output
对每个数据,你需要输出一行。如果P! Q都是传递的,那么请输出’T’。否则, 请输出’N’ (均不包括引号)。
Sample Input
Sample Output
思路:按照规则画画图可以知道,如果是传递图,是没有那个点的深度是大于2的,所以每个点bfs,如果出现深度大于2就结束(N),用过蛮暴力的方式:利用邻接矩阵来3个3个点地尝试——3s, bfs——485ms,好一段时间认为只要是间接连通的点,都要有一条直接的边,结果题目只要求任意3个点。
#include
using namespace std;
#define maxn 2050
int n;
char s[maxn][maxn];
char rt[3] = {'P', 'Q'};
vector M[2][maxn];
void add(int id, int u, int v){
M[id][u].push_back(v);
}
struct node{
int to, deep;
};
bool vis[2][maxn], flag;
void bfs(int id, int u){
vis[id][u] = 1;
node now, next;
now.to = u, now.deep = 1;
queue q;
q.push(now);
while(!q.empty()){
now = q.front();
q.pop();
int point = now.to;
//printf("%d %d\n", id, point);
for(int i = 0;i < M[id][point].size();i++){
int son = M[id][point][i];
if(vis[id][son]) continue;
next.to = son, next.deep = now.deep+1;
if(next.deep>=3){
flag = 0;
return;
}
vis[id][son] = 1;
q.push(next);
}
}
}
int main()
{
int T, i, j, k, cnt;
scanf("%d", &T);
while(T--){
for(i = 0;i < maxn;i++){
M[0][i].clear();
M[1][i].clear();
}
memset(vis, 0, sizeof vis);
scanf("%d", &n);
for(i = 1;i <= n;i++) scanf("%s", s[i]+1);
for(i = 1;i <= n;i++){
for(j = 1;j <= n;j++){
if(s[i][j]=='P'){
add(0, i, j);
}
else if(s[i][j]=='Q') {
add(1, i, j);
}
}
}
flag = 1;
for(i = 1;i <= n;i++){
if(vis[0][i]&&vis[1][i]) continue;
if(!vis[0][i]) bfs(0, i);
if(!flag) break;
if(!vis[1][i]) bfs(1, i);
if(!flag) break;
}
if(!flag) printf("N\n");
else printf("T\n");
}
}