『数学推导』CF15E Triangles
P r o b l e m \mathrm{Problem} Problem
Last summer Peter was at his granny's in the country, when a wolf attacked sheep in the nearby forest. Now he fears to walk through the forest, to walk round the forest, even to get out of the house. He explains this not by the fear of the wolf, but by a strange, in his opinion, pattern of the forest that has n n n levels, where n n n is an even number.
In the local council you were given an area map, where the granny's house is marked by point H H H , parts of dense forest are marked grey (see the picture to understand better).
After a long time at home Peter decided to yield to his granny's persuasions and step out for a breath of fresh air. Being prudent, Peter plans the route beforehand. The route, that Peter considers the most suitable, has the following characteristics:
- it starts and ends in the same place — the granny's house;
- the route goes along the forest paths only (these are the segments marked black in the picture);
- the route has positive length (to step out for a breath of fresh air Peter has to cover some distance anyway);
- the route cannot cross itself;
- there shouldn't be any part of dense forest within the part marked out by this route;
You should find the amount of such suitable oriented routes modulo 1000000009.
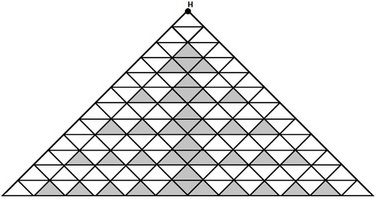 The example of the area map for n = 12 n=12 n=12 is given in the picture. Since the map has a regular structure, you can construct it for other n n n by analogy using the example.
The example of the area map for n = 12 n=12 n=12 is given in the picture. Since the map has a regular structure, you can construct it for other n n n by analogy using the example.
给定一个有规律的金字塔形的图形,其中一部分三角形是黑色的(见图)。 要求统计所有从最顶端出发,沿着黑线走了一条闭合简单路径又回到最顶端,且没有任何黑色三角形在闭合简单路径内部的路径条数
S o l u t i o n \mathrm{Solution} Solution
为了叙述方便,我们不妨将第 2 i − 1 2i-1 2i−1和第 2 i 2i 2i层看作第 i i i层。
当我们只经过第一层时,顺时针和逆时针各有 5 5 5 种方法,即 10 10 10 种。

我们设 a n s \mathrm{ans} ans为从第一层某一个点下去,再从另外某个点上来的方案数。具体的,我们可以表示为以下路径:
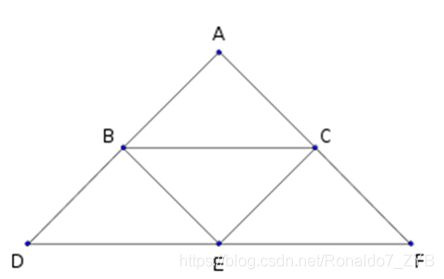
- 从边上下去,中间某点上来的路径有: A B D . . . E F C A , A C D . . . E C A \mathrm{ABD...EFCA ,ACD...ECA} ABD...EFCA,ACD...ECA
- 从中间下去,边上某点上来的路径有: A B E . . . F C A , A B D E . . . F C A \mathrm{ABE...FCA,ABDE...FCA} ABE...FCA,ABDE...FCA
- 从边上下去,边上上来的路径: A B D . . . E . . . F C A \mathrm{ABD...E...FCA} ABD...E...FCA.
对于前四种逆时针路径中,答案显然为 a n s \mathrm{ans} ans,加上顺时针的贡献,贡献为 8 × a n s \mathrm{8\times ans} 8×ans.对于最后一种路径中,逆时针的贡献为 a n s 2 \mathrm{ans^2} ans2.加上顺时针同样为 2 × a n s 2 \mathrm{2\times ans^2} 2×ans2。
则这些路径的总贡献为: 8 × a n s + 2 × a n s 2 + 10 \mathrm{8\times ans + 2\times ans^2 + 10} 8×ans+2×ans2+10
这样,我们就把问题转化为了如何求解计算 a n s \mathrm{ans} ans。
无论你是先从外面进从中间回来,还是从中间进去外面回来,总有一条路径面临着进入中间“凹糟”(不知道怎么形容) 的机会。考虑某一层的凹槽,发现第 i i i 层最多往里面走 i − 2 i-2 i−2 格。
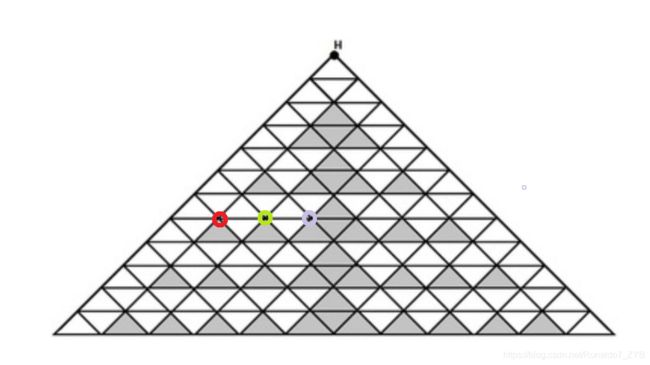 如图,第四层最多完里面走 3 3 3格,并且我们标记了 3 3 3 个决策点。
如图,第四层最多完里面走 3 3 3格,并且我们标记了 3 3 3 个决策点。
- 红色的点可以选择进去和不进去,不进去只有右上反向,而进去则可以选择直接向右,或者先向右下再向右上。这样有两种方案。
- 到了绿色的决策点,可以有两种方案前进,也有两种方案返回。(直接往左上再向左返回,或先向右上,再往左返回)
- 紫色决策点只有两种方案返回。
因此,如果我们往里面前进了 i i i个格子,就有 2 × 2 i = 2 i + 1 2\times 2^i=2^{i+1} 2×2i=2i+1种方案。
那么我们经过了第 k k k层,就一共了 1 + ∑ i = 1 x − 2 2 i + 1 = 2 x − 3 1+\sum_{i=1}^{x-2} 2^{i+1}=2^x-3 1+i=1∑x−22i+1=2x−3
观察到我们到了金字塔的底部,我们还要进行返回操作。
 因此就得到了 a n s \mathrm{ans} ans的计算方式: a n s = ∑ i = 2 k [ 4 × ∑ j = 2 i ( 2 j − 3 ) ] \mathrm{ans}=\sum_{i=2}^{k} [4\times \sum_{j=2}^{i}(2^j-3)] ans=i=2∑k[4×j=2∑i(2j−3)]
因此就得到了 a n s \mathrm{ans} ans的计算方式: a n s = ∑ i = 2 k [ 4 × ∑ j = 2 i ( 2 j − 3 ) ] \mathrm{ans}=\sum_{i=2}^{k} [4\times \sum_{j=2}^{i}(2^j-3)] ans=i=2∑k[4×j=2∑i(2j−3)]
C o d e \mathrm{Code} Code
#include