机器人学回炉重造（5-2）：关节空间规划方法——梯形加减速（与抛物线拟合的线性函数）、S型曲线规划

写在前面

前面的几种多项式规划方法机器人学回炉重造（5）：关节空间规划方法——多项式轨迹（三次多项式、五次多项式、抛物线轨迹）都存在没有最大速度和最大加速度限制的问题，当机械系统存在速度和加速度限制范围时，上述方法就不太适合。下面的梯形加减速和S型曲线就不会存在这种问题。

梯形加减速（与抛物线拟合的线性函数）

梯形曲线在电机控制中经常被用到，因为其速度曲线形状为梯形，因此被称为梯形速度曲线。
一般情况下，用户给定起始速度、终止速度、加速度、减速度、最大速度以及起始时刻和终止时刻的位移参数，需要计算出加速段、匀速段以及减速段对应的时间Ta、Tv、Td，然后再根据位移、速度以及加速度公式计算轨迹。
（1）首先需要计算用户给定参数下所能达到的最大速度。要使能够达到的速度最大，则只有加速段和减速段，没有匀速段。此时h = p1 - p0，有如下公式

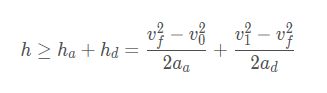
根据上述公式，可得到给定参数下所能达到的最大速度：

（2）比较理论最大速度vf与用户限定最大速度vmax之间的大小。当vf时，说明系统能够达到的最大速度无法满足用户要求，此时匀速段的最大速度为vv = vf；当vf>vmax时，说明给定的参数可以达到用户限定的最大速度，但是又不能超过限定的最大速度，因此匀速段的最大速度为vv = vmax。
（3）计算加速段、匀速段以及减速段的时间和位移，计算公式如下：

（4）计算各时刻下的位移、速度以及加速度，公式如下：


%% 与抛物线拟合的线性函数（线性轨迹）
% 梯形加减速，可限制最大速度和最大加速度
% 用户给定起始速度、终止速度、加速度、减速度、最大速度及位移参数
% 该算法需要计算出加速段、匀速段以及减速段对应的时间Ta Tv Td
% t0 = 0, p0 = 5, p1 = 30, v0 = 50, vmax = 150, v1 = 20, aa = 1000
% ad = -1500
t0 = 2;
p0 = 5; p1 = 30;
v0 = 50; vmax = 150; v1 = 20;
aa = 1000; ad = -1500;
h = p1 - p0;
% 可达到的最大速度
vf = sqrt((2.0*aa*ad*h - aa*v1^2 + ad*v0^2) / (ad - aa));
% 确定匀速阶段速度
if (vf < vmax)
    vv = vf;
else
    vv = vmax;
end
% 计算加速阶段的时间和位移
Ta = (vv - v0) / aa;
La = v0*Ta + (1.0/2.0)*aa*Ta^2;
% 计算匀速阶段的时间和位移
Tv = (h - (vv^2 - v0^2)/(2.0*aa) - (v1^2 - vv^2)/(2.0*ad)) / vv;
Lv = vv*Tv;
% 计算减速阶段的时间和位移
Td = (v1 - vv) / ad;
Ld = vv*Td + (1.0/2.0)*ad*Td^2;
k = 1;
ts = 0.001;
% 计算轨迹的离散点
for t = t0: ts: (t0+Ta+Tv+Td)
    time(k) = t;
    t = t - t0;
    if (t >= 0 && t < Ta)
        p(k) = p0 + v0*t + (1.0/2.0)*aa*t^2;
        pd(k) = v0 + aa*t;
        pdd(k) = aa;
    elseif (t >= Ta && t < Ta+Tv)
        p(k) = p0 + La + vv*(t - Ta);
        pd(k) = vv;
        pdd(k) = 0;
    elseif (t >= Ta+Tv && t <= Ta+Tv+Td)
        p(k) = p0 + La + Lv + vv*(t - Ta - Tv) + (1.0/2.0)*ad*power(t - Ta - Tv, 2);
        pd(k) = vv + ad*(t - Ta - Tv);
        pdd(k) = ad;
    end
    k = k + 1;
end
figure(1)
subplot(3, 1, 1)
plot(time, p, 'r', 'LineWidth', 1.5)
ylabel('position')
grid on
subplot(3, 1, 2)
plot(time, pd, 'b', 'LineWidth', 1.5)
ylabel('velocity')
grid on
subplot(3, 1, 3)
plot(time, pdd, 'g', 'LineWidth', 1.5)
ylabel('acceleration')
grid on

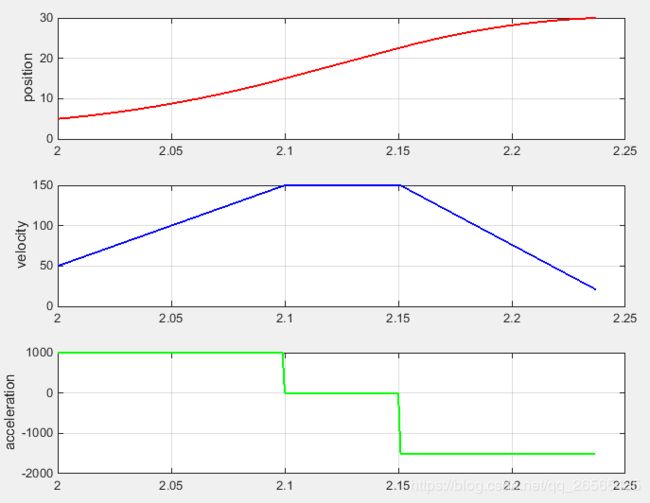
由上图可以看出，梯形曲线在t0、Ta、Ta+Tv以及Ta+Tv+Td时刻时加速度不连续，速度过渡不平滑，存在冲击，这是梯形曲线的缺点，因此该加减速曲线常用于低速、低成本的运动控制过程。下面的S型曲线能解决这个问题。

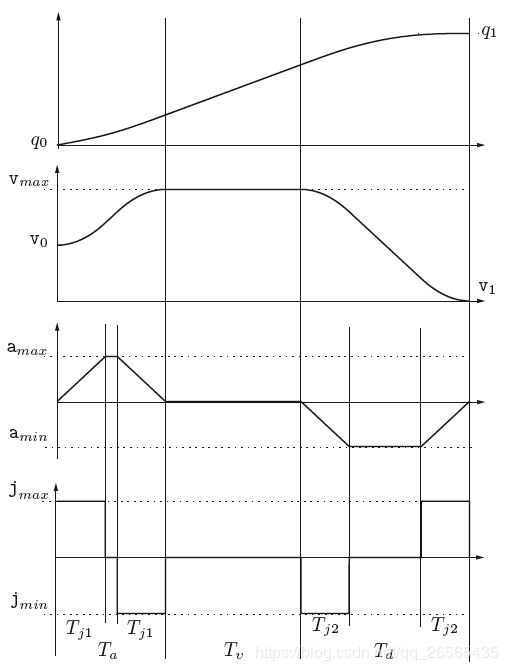
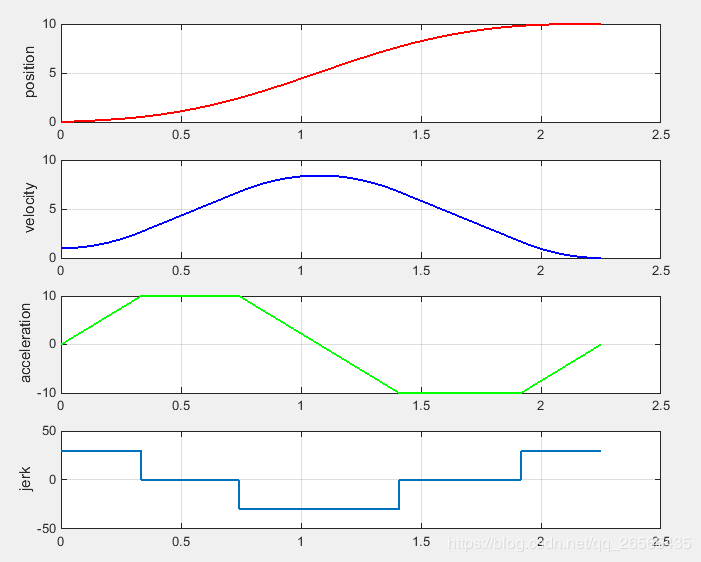
S型曲线

定义：

• 加速段 0 <= t < Ta：
  • 以恒定的jerk J（加速度的导数）使加速度从0增加到预先设定的a；
  • 以恒定的加速度加速；
  • 已恒定的负的jerk J（加速度的导数）使加速度从预先设定的a减到0；
• 最大速度段 Ta <= t < Ta + Tv：
  • 以恒定的速度v匀速运动；
• 减速段 Ta + Tv <= t <= Ta + Tv + Td：
  • 已恒定的负的jerk J（加速度的导数）使加速度从0减到预先设定的-a；
  • 以恒定的加速度-a减速；
  • 以恒定的jerk J（加速度的导数）使加速度从预先设定的-a增加到0；

总的运行段数为七段，因此S型曲线也成为七段式曲线。

下面是S曲线的算法步骤：

第一步：由于初始时刻和终止时刻的位置存在谁大谁小的问题，即q0q1，这会对最后的轨迹曲线造成影响。需经如下处理：

然后进行第二步；
第二步：判断是否能够达到最大速度，步骤如下：


此时得到匀速时间Tv，进行第三步；

第三步：如果Tv > 0，则跳转到第四步；反之，则跳转到第五步；

第四步：此时满足条件Tv > 0，说明系统能够达到的最大速度与设定的最大速度相等，即vlim = vmax，存在匀速时间，整理计算得到Ta、Tv、Td、Tj1、Tj2直接跳转到第十一步计算轨迹；

第五步：此时满足Tv <= 0，说明系统不能达到指定的最大速度vlim < vmax，系统不存在匀速段。此时Tv = 0。此时先假设系统能够达到最大加速度和最小加速度，进行如下计算：

得到Ta、Td，对两者进行讨论，进行第六步；

第六步：判断Ta <0 or Td < 0?，如果Ta < 0 || Td < 0，则跳转第七步；反之，则跳转至第八步；

第七步：满足Ta < 0 || Td < 0的条件。如果此时Ta < 0，令Ta = 0，说明系统没有加速度段，只有减速段，减速段参数利用如下公式计算：

此时得到Ta、Tj，跳转至第十一步直接计算轨迹；
如果Td < 0，令Td = 0，说明系统没有减速段，只有加速段，加速段参数利用如下公式计算：

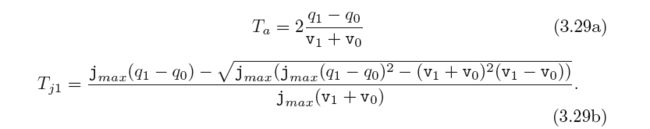
此时得到Td、Tj，跳转至第十一步直接计算轨迹；

第八步：判断Ta >= 2Tj && Td >= 2Tj是否成立，如果成立则跳转至第九步；反之，则跳转至第十步；

第九步：此时Ta >= 2Tj && Td >= 2Tj，说明系统的加速段和减速段均能达到最大加速度，整理（3.26a）、（3.26b）、（3.26c）得到的Ta、Td和Tj，直接跳转至第十一步计算轨迹；

第十步：系统加速和减速阶段至少有一段不能达到最大加速度，这种情况很少见，处理方法为逐渐减小amax，令amax = lambda*amax(0（这种方法不是最优，但是从计算的角度可以接受），然后跳转至第第五步进行循环，循环结束条件为Ta >= 2Tj && Td >= 2Tj成立。这一步也体现了本文S曲线规划的缺点，一旦出现第十步的情况，则无法获得最优规划曲线，也就是在指定的参数范围内，无法获得时间最短的轨迹。

第十一步：计算位置、速度、加速度以及加加速度轨迹曲线，公式如下，此时假设t0 = 0：

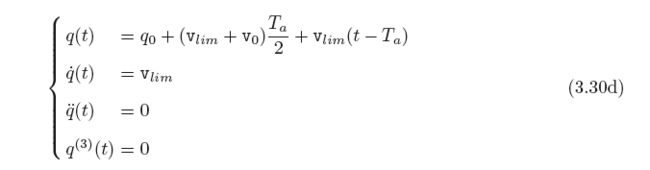
S曲线流程图

配合流程图，更容易理解上述计算步骤：

Matlab实现程序

% 单关节空间规划
%% S曲线参数计算（S型速度规划，又称七段式轨迹）
function para = STrajectoryPara(q0, q1, v0, v1, vmax, amax, jmax)
% 得到规划参数Ta, Tv, Td, Tj1, Tj2, q0, q1, v0, v1, vlim, amax, amin, alima, alimd, jmax, jmin
% 用户给定参数
% 边界条件q0 = 10, q1 = 0, v0 = -7, v1 = 0
% 约束条件vmax = 10, amax = 10, jamx = 30
% q0 = 0; q1 = 10; 
% v0 = 7.5; v1 = 0;
% vmax = 10; amax = 10; jmax = 30;
vmin = -vmax; amin = -amax; jmin = -jmax;

%% 利用公式（3.31）（3.32）转化得到实际的q_0、q_1、v_max、a_max
sigma = sign(q1 - q0);  
q_0 = sigma*q0;
q_1 = sigma*q1;
v_0 = sigma*v0;
v_1 = sigma*v1;
v_max = ((sigma+1)/2)*vmax + ((sigma-1)/2)*vmin;
v_min = ((sigma+1)/2)*vmin + ((sigma-1)/2)*vmax;
a_max = ((sigma+1)/2)*amax + ((sigma-1)/2)*amin;
a_min = ((sigma+1)/2)*amin + ((sigma-1)/2)*amax;
j_max = ((sigma+1)/2)*jmax + ((sigma-1)/2)*jmin;
j_min = ((sigma+1)/2)*jmin + ((sigma-1)/2)*jmax;

%% 判断是否达到最大速度
if ((v_max - v_0)*j_max < a_max^2) 
    Tj1 = sqrt((v_max - v_0) / j_max); % 达不到a_max
    Ta = 2*Tj1;
    a_lima = j_max * Tj1;
else
    Tj1 = a_max / j_max; % 能够达到a_max
    Ta = Tj1 + (v_max - v_0) / a_max;
    a_lima = a_max;
end
if ((v_max - v_1)*j_max < a_max^2)
    Tj2 = sqrt((v_max - v_1) / j_max); % 达不到a_min
    Td = 2*Tj2;
    a_limd =  -j_max * Tj2;
else
    Tj2 = a_max / j_max; % 能够达到a_min
    Td = Tj2 + (v_max - v_1) / a_max;
    a_limd = -a_max;
end
% 根据（3.25）计算匀速段时间
Tv = (q_1 - q_0)/v_max - (Ta/2)*(1 + v_0/v_max) - (Td/2)*(1 + v_1/v_max);

%% 对Tv进行讨论
if (Tv > 0)
    % 达到最大速度v_max，即存在匀速阶段
    vlim = v_max;
    T = Ta + Tv + Td;
    para = [Ta, Tv, Td, Tj1, Tj2, q_0, q_1, v_0, v_1, vlim, a_max, a_min, a_lima, a_limd, j_max, j_min];
    return;
else
    % 达不到最大速度，即匀速阶段Tv=0
    % 假设最大加速度和最小加速度均能达到
    Tv = 0;
    Tj = a_max / j_max;
    Tj1 = Tj;
    Tj2 = Tj;
    delta = (a_max^4/j_max^2) + 2*(v_0^2 + v_1^2) + a_max*(4*(q_1 - q_0) - 2*(a_max/j_max)*(v_0 + v_1));
    Ta = ((power(a_max, 2)/j_max) - 2.0*v_0 + sqrt(delta)) / (2.0*a_max);
    Td = ((power(a_max, 2)/j_max) - 2.0*v_1 + sqrt(delta)) / (2.0*a_max);
    % 对Ta和Td进行讨论
    if (Ta < 0 || Td < 0)
        if (Ta < 0)
            % 没有加速段，只有减速段
            Ta = 0; Tj1 = 0;
            Td = 2*(q_1 - q_0) / (v_0 + v_1);
            Tj2 = (j_max*(q_1 - q_0) - sqrt(j_max*(j_max*power(q_1 - q_0, 2) + power(v_1 + v_0, 2)*(v_1 - v_0)))) / (j_max*(v_1 + v_0));
            a_lima = 0;
            a_limd = -j_max*Tj2;
            vlim = v0;
            para = [Ta, Tv, Td, Tj1, Tj2, q_0, q_1, v_0, v_1, vlim, a_max, a_min, a_lima, a_limd, j_max, j_min];
            return;
        elseif (Td < 0)
            % 没有减速段，只有加速段
            Td = 0; Tj2 = 0;
            Ta = 2*(q_1 - q_0) / (v_0 + v_1);
            Tj1 = (j_max*(q_1 - q_0) - sqrt(j_max*(j_max*power(q_1 - q_0, 2)) - power(v_1 + v_0, 2)*(v_1 - v_0))) / (j_max*(v_1 + v_0));
            a_lima = j_max*Tj1;
            a_limd = 0;
            vlim = v_0 + a_lima*(Ta - Tj1);
            para = [Ta, Tv, Td, Tj1, Tj2, q_0, q_1, v_0, v_1, vlim, a_max, a_min, a_lima, a_limd, j_max, j_min];
            return;
        end
    elseif (Ta >= 2*Tj && Td >= 2*Tj)
        % 加速段和减速段都能达到最大加速度
        a_lima = a_max;
        a_limd = -a_max;
        vlim = v0 + a_lima*(Ta - Tj);
        para = [Ta, Tv, Td, Tj1, Tj2, q_0, q_1, v_0, v_1, vlim, a_max, a_min, a_lima, a_limd, j_max, j_min];
        return;
    else
        % 加速和减速阶段至少有一段不能达到最大加速度
        lambda = 0.99; % 系统取0= 2*Tj && Td >= 2*Tj)
                % 加速段和减速段都能达到最大加速度
                a_lima = a_max;
                a_limd = -a_max;
                vlim = v0 + a_lima*(Ta - Tj);
                para = [Ta, Tv, Td, Tj1, Tj2, q_0, q_1, v_0, v_1, vlim, a_max, a_min, a_lima, a_limd, j_max, j_min];
                return;
            end
        end
    end
end
end

%% 计算位移
function q = S_position(t, Ta, Tv, Td, Tj1, Tj2, q0, q1, v0, v1, vlim, amax, amin, alima, alimd, jmax, jmin)
T = Ta + Tv + Td;
% 加速段
if (t >= 0 && t < Tj1)
    q = q0 + v0*t + jmax*t^3/6;
elseif (t >= Tj1 && t < Ta - Tj1)
    q = q0 + v0*t +(alima/6)*(3*t^2 - 3*Tj1*t + Tj1^2);
elseif (t >= Ta - Tj1 && t < Ta)
    q = q0 + (vlim + v0)*(Ta/2) - vlim*(Ta - t) - jmin*((Ta - t)^3/6);
% 匀速段
elseif (t >= Ta && t < Ta + Tv)
    q = q0 + (vlim + v0)*(Ta/2) + vlim*(t - Ta);
% 减速段
elseif (t >= Ta + Tv && t < T - Td + Tj2)
    q = q1 - (vlim + v1)*(Td/2) + vlim*(t - T + Td) - jmax*(power(t - T + Td, 3)/6);
elseif (t >= T - Td + Tj2 && t < T - Tj2)
    q = q1 - (vlim + v1)*(Td/2) + vlim*(t - T + Td) + (alimd/6)*(3*power(t - T + Td, 2) - 3*Tj2*(t - T + Td) + Tj2^2);
elseif (t >= T - Tj2 && t <= T)
    q = q1 - v1*(T - t) - jmax*(power(T - t, 3)/6);
end
end


%% 计算速度
function qd = S_velocity(t, Ta, Tv, Td, Tj1, Tj2, q0, q1, v0, v1, vlim, amax, amin, alima, alimd, jmax, jmin)
T = Ta + Tv + Td;
if (t >= 0 && t < Tj1)
    qd = v0 + jmax*(t^2/2);
elseif (t >= Tj1 && t < Ta - Tj1)
    qd = v0 + alima*(t - Tj1/2);
elseif (t >= Ta - Tj1 && t < Ta)
    qd = vlim + jmin*(power(Ta - t, 2)/2);
% 匀速段
elseif (t >= Ta && t < Ta + Tv)
    qd = vlim;
% 减速段
elseif (t >= Ta + Tv && t < T - Td + Tj2)
    qd = vlim - jmax*(power(t - T + Td, 2)/2);
elseif (t >= T - Td + Tj2 && t < T - Tj2)
    qd = vlim + alimd*(t - T + Td - Tj2/2);
elseif (t >= T - Tj2 && t <= T)
    qd = v1 + jmax*(power(t - T, 2)/2);
end
end


%% 计算加速度
function qdd = S_acceleration(t, Ta, Tv, Td, Tj1, Tj2, q0, q1, v0, v1, vlim, amax, amin, alima, alimd, jmax, jmin)
T = Ta + Tv + Td;
if (t >= 0 && t < Tj1)
    qdd = jmax*t;
elseif (t >= Tj1 && t < Ta - Tj1)
    qdd = alima;
elseif (t >= Ta - Tj1 && t < Ta)
    qdd = -jmin*(Ta - t);
% 匀速段
elseif (t >= Ta && t < Ta + Tv)
    qdd = 0;
% 减速段
elseif (t >= Ta + Tv && t < T - Td + Tj2)
    qdd = -jmax*(t - T + Td);
elseif (t >= T - Td + Tj2 && t < T - Tj2)
    qdd = alimd;
elseif (t >= T - Tj2 && t <= T)
    qdd = -jmax*(T - t);
end
end


%% 计算加加速度
function qddd = S_jerk(t, Ta, Tv, Td, Tj1, Tj2, q0, q1, v0, v1, vlim, amax, amin, alima, alimd, jmax, jmin)
T = Ta + Tv + Td;
if (t >= 0 && t < Tj1)
    qddd = jmax;
elseif (t >= Tj1 && t < Ta - Tj1)
    qddd = 0;
elseif (t >= Ta - Tj1 && t < Ta)
    qddd = jmin;
% 匀速段
elseif (t >= Ta && t < Ta + Tv)
    qddd = 0;
% 减速段
elseif (t >= Ta + Tv && t < T - Td + Tj2)
    qddd = -jmax;
elseif (t >= T - Td + Tj2 && t < T - Tj2)
    qddd = 0;
elseif (t >= T - Tj2 && t <= T)
    qddd = jmax;
end
end

测试程序

%% S曲线规划
% 边界条件
q0 = 0; q1 = 10; 
v0 = 1; v1 = 0;
vmax = 10; amax = 10; jmax = 30;
sigma = sign(q1 - q0);
% 得到规划参数Ta, Tv, Td, Tj1, Tj2, q0, q1, v0, v1, vlim, amax, amin, alima, alimd, jmax, jmin
para = STrajectoryPara(q0, q1, v0, v1, vmax, amax, jmax)
i = 1; 
T = para(1) + para(2) + para(3)
for t = 0: 0.001: T
   time(i) = 0.001*i;
   q(i) = S_position(t, para(1), para(2), para(3), para(4), para(5), para(6), para(7), para(8), para(9), para(10), para(11), para(12), para(13), para(14), para(15), para(16));
   qd(i) = S_velocity(t, para(1), para(2), para(3), para(4), para(5), para(6), para(7), para(8), para(9), para(10), para(11), para(12), para(13), para(14), para(15), para(16));
   qdd(i) = S_acceleration(t, para(1), para(2), para(3), para(4), para(5), para(6), para(7), para(8), para(9), para(10), para(11), para(12), para(13), para(14), para(15), para(16));
   qddd(i) = S_jerk(t, para(1), para(2), para(3), para(4), para(5), para(6), para(7), para(8), para(9), para(10), para(11), para(12), para(13), para(14), para(15), para(16));
   i = i + 1;
end
q = sigma*q;
qd = sigma*qd;
qdd = sigma*qdd;
qddd = sigma*qddd;
figure(1)
subplot(4, 1, 1)
plot(time, q, 'r', 'LineWidth', 1.5)
grid on
subplot(4, 1, 2)
plot(time, qd, 'b', 'LineWidth', 1.5)
grid on
subplot(4, 1, 3)
plot(time, qdd, 'g', 'LineWidth', 1.5)
grid on
subplot(4, 1, 4)
plot(time, qddd, 'LineWidth', 1.5)
grid on

---

参考

S型速度规划
Trajectory Planning for Automatic Machines and Robots

---

2019.11.27——发现两处错误，STrajectoryPara.m中第86行、128行程序出错，已改正为vlim = v_0 + a_lima*(Ta - Tj1)